Rozwiązanie
Krok 1. Obliczenie długości odcinka \(AB\).
Aby dowiedzieć się, czy punkt \(B\) należy do koła, to musimy sprawdzić jaka jest odległość od punktu \(A\) do punktu \(B\). Jeżeli ta odległość jest mniejsza lub równa promieniowi koła, to punkt \(B\) będzie leżeć w kole. Jeżeli ta odległość jest większa od długości promienia, to punkt \(B\) będzie poza kołem.
Aby obliczyć długość odcinka \(AB\) możemy skorzystać z Twierdzenia Pitagorasa:
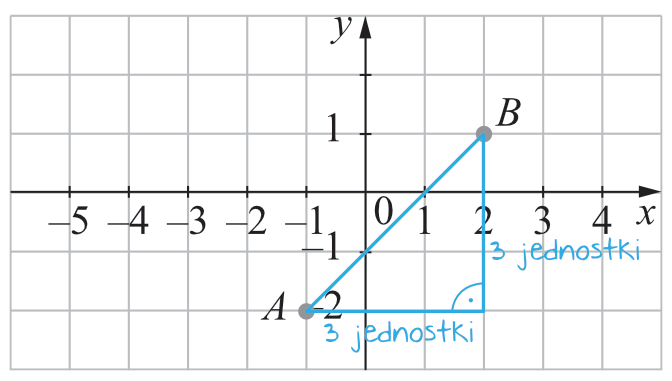
Nasz odcinek \(AB\) jest przeciwprostokątną trójkąta o przyprostokątnych równych \(3\), zatem:
$$3^2+3^2=|AB|^2 \\
9+9=|AB|^2 \\
|AB|^2=18 \\
|AB|=\sqrt{18} \quad\lor\quad |AB|=-\sqrt{18}$$
Ujemną długość oczywiście odrzucamy, bo długość odcinka jest na pewno dodatnia, zatem wiemy już, że \(AB=\sqrt{18}\). Na upartego moglibyśmy jeszcze wyłączyć czynnik przez znak pierwiastka i zapisać, że \(AB=3\sqrt{2}\), ale nie jest to konieczne, bo postać \(\sqrt{18}\) będzie dla nas za chwilę bardzo pożyteczna.
Krok 2. Ustalenie, czy punkt \(B\) leży w kole.
Promień naszego koła to \(r=4\). Odległość od punktu \(A\) do punktu \(B\) wynosi \(\sqrt{18}\). Powinniśmy dostrzec, że \(\sqrt{18}\) jest na pewno większy od \(4\). Skąd to wiemy? Po prostu \(\sqrt{16}=4\), więc \(\sqrt{18}\) musi być większy od \(4\). To oznacza, że punkt \(B\) znajduje się poza kołem.