Rozwiązanie
Krok 1. Obliczenie długości boku rombu.
Romb na cztery boki równej długości, zatem skoro jego obwód jest równy \(24 cm\), to każdy bok ma:
$$a=24cm:4 \\
a=6cm$$
Krok 2. Sporządzenie rysunku pomocniczego.
Pamiętając o tym, że przekątne rombu przecinają się pod kątem prostym i w połowie swojej długości, otrzymamy taką oto sytuację:
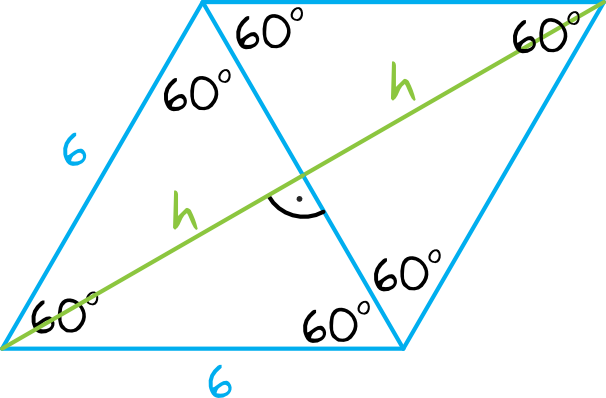
Można więc powiedzieć, że po dorysowaniu krótszej przekątnej powstały nam na rysunku dwa trójkąty równoboczne.
Krok 3. Obliczenie długości dłuższej przekątnej.
Z rysunku wynika, że do obliczenia długości dłuższej przekątnej przyda nam się wyznaczenie wysokości trójkąta równobocznego, który nam powstał. Korzystając ze wzoru na wysokość trójkąta równobocznego, możemy zapisać, że:
$$h=\frac{a\sqrt{3}}{2} \\
h=\frac{6\sqrt{3}cm}{2} \\
h=3\sqrt{3}cm$$
Dłuższa przekątna będzie dwa razy dłuższa od wysokości takiego trójkąta (co widać na rysunku), czyli będzie miała ona długość:
$$2\cdot3\sqrt{3}cm=6\sqrt{3}cm$$