W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa \(\frac{5\sqrt{3}}{4}\), a pole powierzchni bocznej tego ostrosłupa jest równe \(\frac{15\sqrt{3}}{4}\). Oblicz objętość tego ostrosłupa.
Wiemy, że wszystkie ściany boczne mają łączną powierzchnię równą \(\frac{15\sqrt{3}}{4}\). Skoro są trzy takie ściany, to każda z nich ma pole powierzchni równe:
$$P_{śb}=\frac{15\sqrt{3}}{4}:3=\frac{5\sqrt{3}}{4}$$
W podstawie ostrosłupa mamy trójkąt równoboczny, bo jest to ostrosłup prawidłowy trójkątny. To oznacza, że każda ściana boczna jest trójkątem o podstawie \(a\) oraz wysokości \(h=\frac{5\sqrt{3}}{4}\) (wysokość jest podana w treści zadania). Skoro tak, to z pola trójkąta możemy wyznaczyć długość krawędzi \(a\):
$$P_{śb}=\frac{1}{2}a\cdot h \\
\frac{5\sqrt{3}}{4}=\frac{1}{2}a\cdot\frac{5\sqrt{3}}{4} \quad\bigg/:\frac{5\sqrt{3}}{4} \\
1=\frac{1}{2}a \\
a=2$$
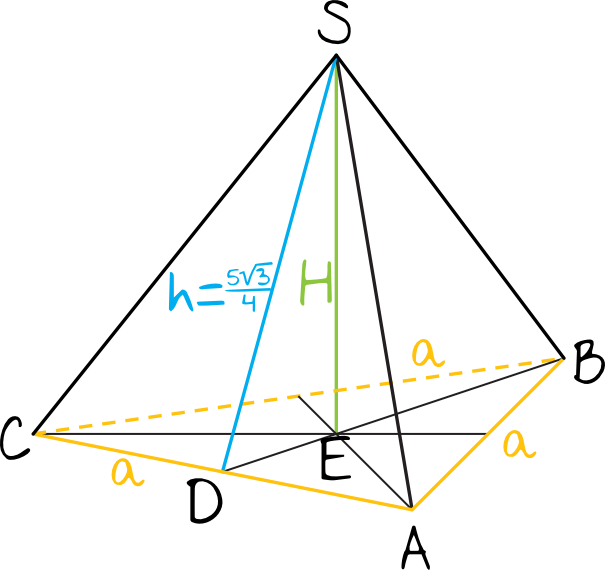
Odcinek \(DE\) stanowi \(\frac{1}{3}\) długości wysokości trójkąta równobocznego (czyli odcinka \(DB\)) znajdującego się w podstawie. Ze wzorów na wysokość trójkąta równobocznego wiemy, że:
$$|DB|=\frac{a\sqrt{3}}{2} \\
|DB|=\frac{2\sqrt{3}}{2} \\
|DB|=\sqrt{3}$$
Skoro odcinek \(DE\) ma stanowić \(\frac{1}{3}\) długości odcinka \(DB\), to:
$$|DE|=\frac{1}{3}\cdot\sqrt{3}=\frac{\sqrt{3}}{3}$$
Skorzystamy tutaj z Twierdzenia Pitagorasa w trójkącie \(DES\):
$$|DE|^2+|SE|^2=|DS|^2 \\
\left(\frac{\sqrt{3}}{3}\right)^2+|SE|^2=\left(\frac{5\sqrt{3}}{4}\right)^2 \\
\frac{3}{9}+|SE|^2=\frac{25\cdot3}{16} \\
\frac{1}{3}+|SE|^2=\frac{75}{16} \\
\frac{16}{48}+|SE|^2=\frac{225}{48} \\
|SE|^2=\frac{225}{48}-\frac{16}{48} \\
|SE|^2=\frac{209}{48} \\
|SE|=\sqrt{\frac{209}{48}}=\frac{\sqrt{209}}{4\sqrt{3}}=\frac{\sqrt{209}\cdot\sqrt{3}}{4\sqrt{3}\cdot\sqrt{3}}=\frac{\sqrt{627}}{12}$$
Pole trójkąta równobocznego znajdującego się w podstawie obliczymy według wzoru:
$$P_{p}=\frac{a^2\sqrt{3}}{4} \\
P_{p}=\frac{2^2\sqrt{3}}{4} \\
P_{p}=\frac{4\sqrt{3}}{4} \\
P_{p}=\sqrt{3}$$
Skoro \(P_{p}=\sqrt{3}\) oraz \(H=\frac{\sqrt{627}}{12}\), to objętość ostrosłupa będzie równa:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\sqrt{3}\cdot\frac{\sqrt{627}}{12} \\
V=\frac{1}{3}\sqrt{3}\cdot\frac{\sqrt{209}\cdot\sqrt{3}}{12} \\
V=\frac{1}{3}\cdot\frac{\sqrt{209}\cdot3}{12} \\
V=\frac{\sqrt{209}}{12}$$
\(V=\frac{\sqrt{209}}{12}\)


Dlaczego przy obliczaniu V w pierwszej liczbie znika pierwiastek z 3 a w drugiej pojawia się 3 w liczniku?
√627 rozbiłem na mnożenie pierwiastek √209 razy √3. Zrobiłem to po to, by pomnożyć √3 (stojący przy ułamku 1/3) przez √3 który będziemy mieć w liczniku, bo wiemy że √3 razy √3 to jest 3.
Gdybym sobie tego nie rozbił, to prędzej czy później musiałbym pomnożyć √3 przez √627 i miałbym kosmiczny √1881 z którego potem trzeba byłoby wyłączać czynnik przed znak pierwiastka, by otrzymać jakąś sensowną postać ;)