Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Aby przystąpić do obliczeń sporządźmy prosty rysunek pomocniczy, zaznaczając na nim dane z treści zadania:
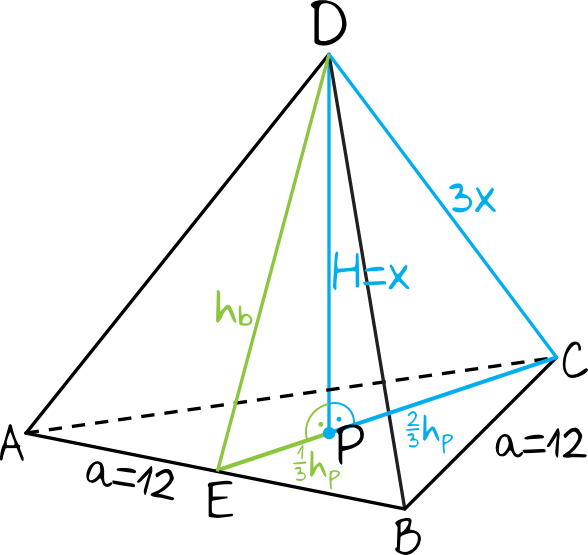
Krok 2. Obliczenie wysokości trójkąta znajdującego się w podstawie.
Ostrosłup jest prawidłowy, zatem w podstawie musi znaleźć się trójkąt równoboczny. Wiemy, że bok tego trójkąta ma długość \(a=12\), zatem wysokość podstawy będzie równa:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
h_{p}=\frac{12\sqrt{3}}{2} \\
h_{p}=6\sqrt{3}$$
Krok 3. Obliczenie długości dolnej przyprostokątnej niebieskiego trójkąta prostokątnego.
Zgodnie z naszym rysunkiem (i zgodnie z własnościami trójkątów równobocznych), dolna przyprostokątna niebieskiego trójkąta prostokątnego stanowi \(\frac{2}{3}\) wysokości trójkąta równobocznego, który znalazł się w podstawie. W związku z tym:
$$PC=\frac{2}{3}h_{p} \\
PC=\frac{2}{3}\cdot6\sqrt{3} \\
PC=4\sqrt{3}$$
Krok 4. Obliczenie wysokości ostrosłupa.
Ponownie spoglądamy na niebieski trójkąt prostokątny. Korzystając z Twierdzenia Pitagorasa możemy teraz zapisać, że:
$$|PC|^2+|PD|^2=|CD|^2 \\
(4\sqrt{3})^2+x^2=(3x)^2 \\
16\cdot3+x^2=9x^2 \\
8x^2=48 \\
x^2=6 \\
x=\sqrt{6} \quad\lor\quad x=-\sqrt{6}$$
Ujemną wartość oczywiście odrzucamy, bo wysokość nie może być ujemna, czyli już wiemy, że wysokość naszego ostrosłupa to \(H=\sqrt{6}\).
Krok 5. Obliczenie długości dolnej przyprostokątnej zielonego trójkąta prostokątnego.
Zgodnie z naszym rysunkiem dolna przyprostokątna zielonego trójkąta prostokątnego ma długość \(\frac{1}{3}\) wysokości trójkąta równobocznego, który znalazł się w podstawie, zatem:
$$EP=\frac{1}{3}h_{p} \\
EP=\frac{1}{3}\cdot6\sqrt{3} \\
EP=2\sqrt{3}$$
Krok 6. Obliczenie wysokości ściany bocznej.
Do obliczenia pola powierzchni bocznej musimy znać wysokość ściany bocznej. W tym celu spoglądamy na nasz zielony trójkąt prostokątny i korzystając z Twierdzenia Pitagorasa otrzymamy:
$$|EP|^2+|PD|^2=|ED|^2 \\
(2\sqrt{3})^2+(\sqrt{6})^2=|ED|^2 \\
4\cdot3+6=|ED|^2 \\
12+6=|ED|^2 \\
|ED|^2=18 \\
|ED|=\sqrt{18} \quad\lor\quad |ED|=-\sqrt{18}$$
Długość odcinka nie może być ujemna, zatem zostaje nam \(|ED|=\sqrt{18}\), co możemy jeszcze rozpisać jako \(|ED|=\sqrt{9\cdot2}=3\sqrt{2}\). To oznacza, że wysokość ściany bocznej jest równa \(h_{b}=3\sqrt{2}\).
Krok 7. Obliczenie objętości ostrosłupa.
Mamy już komplet informacji na temat naszego ostrosłupa. Wiemy, że w podstawie jest trójkąt równoboczny o boku \(a=12\), wiemy też że \(H=\sqrt{6}\), zatem:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot\frac{a^2\sqrt{3}}{4}\cdot H \\
V=\frac{1}{3}\cdot\frac{144\sqrt{3}}{4}\cdot\sqrt{6} \\
V=\frac{1}{3}\cdot\frac{144\sqrt{3}}{4}\cdot\sqrt{6} \\
V=\frac{1}{3}\cdot36\sqrt{3}\cdot\sqrt{6} \\
V=12\sqrt{3}\cdot\sqrt{6} \\
V=12\sqrt{18} \\
V=12\sqrt{9\cdot2} \\
V=12\cdot3\sqrt{2} \\
V=36\sqrt{2}$$
Krok 8. Obliczenie pola powierzchni bocznej.
Na pole powierzchni bocznej składają się \(3\) ściany, każda z nich ma podstawę o długości \(a=12\) oraz wysokość \(h_{b}=3\sqrt{2}\). W związku z tym:
$$P_{b}=3\cdot\frac{1}{2}ah \\
P_{b}=3\cdot\frac{1}{2}\cdot12\cdot3\sqrt{2} \\
P_{b}=18\cdot3\sqrt{2} \\
P_{b}=54\sqrt{2}$$