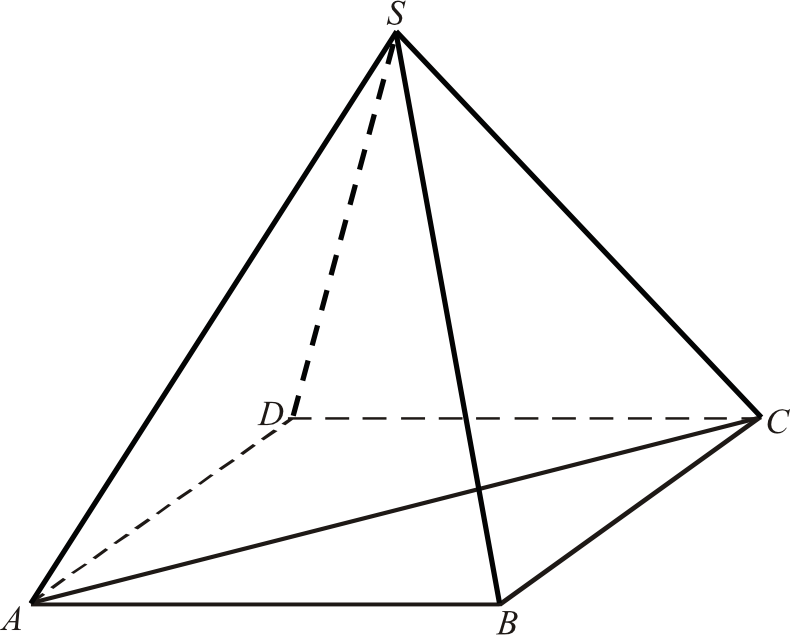
W ostrosłupie prawidłowym czworokątnym \(ABCDS\) (zobacz rysunek) przekątna \(AC\) podstawy ma długość \(4\sqrt{2}\). Kąt \(ASC\) między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę \(60°\). Oblicz objętość tego ostrosłupa.
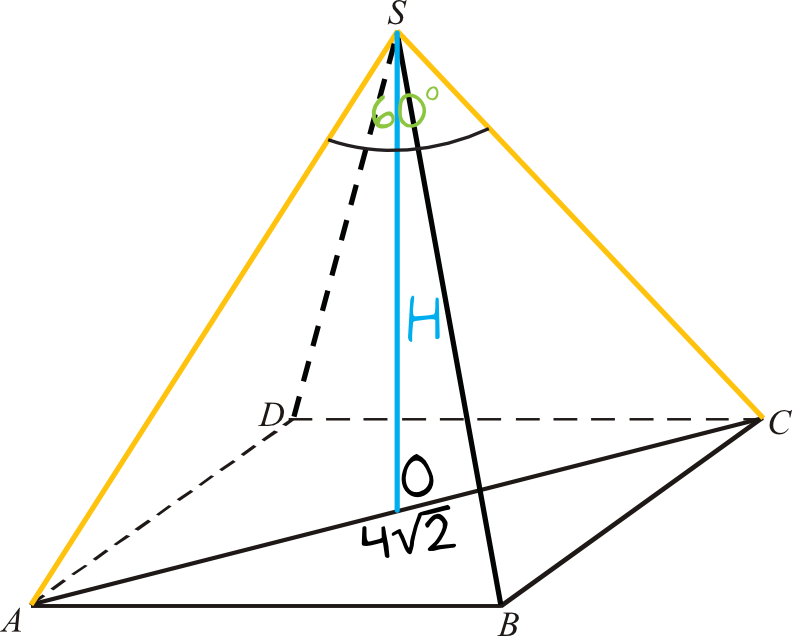
Dorysujmy sobie wysokość naszego ostrosłupa, bo będzie nam ona potrzebna do obliczenia objętości. Widzimy wyraźnie, że wysokość ostrosłupa jest jednocześnie wysokością trójkąta \(ACS\). Skoro jest to ostrosłup prawidłowy czworokątny, to wszystkie ramiona trójkąta \(ACS\) mają tą samą długość (patrz kolor pomarańczowy na rysunku), a więc na pewno jest to trójkąt równoramienny. Ale… okazuje się, że on jest nawet nie tyle równoramienny, co równoboczny. Skąd to wynika? Wiemy, że między pomarańczowymi ramionami kąt ma miarę \(60°\). To oznacza, że kąty przy podstawie muszą mieć łącznie \(180°-60°=120°\). W trójkącie równoramiennym kąty przy podstawie muszą mieć tą samą miarę, czyli każdy z nich ma\(120°:2=60°\). Z tego wynika, że wszystkie kąty trójkąta \(ACS\) będą mieć \(60°\).
Dostrzeżenie tej własności bardzo ułatwia nam rozwiązanie zadania, bo w tablicach mamy bezpośredni wzór na wysokość trójkąta równobocznego. Gdybyśmy nie zauważyli że to trójkąt równoboczny, to moglibyśmy próbować obliczyć wysokość z tangensa w trójkącie \(AOS\).
W podstawie mamy na pewno kwadrat, bo jest to ostrosłup prawidłowy czworokątny. Z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną równą \(a\sqrt{2}\). Długość tej przekątnej jest podana w treści i wynosi \(|AC|=4\sqrt{2}\), zatem w podstawie mamy kwadrat o boku \(4\). To oznacza, że jego pole będzie równe:
$$P_{p}=a^2 \\
P_{p}=4^2 \\
P_{p}=16$$
Z treści zadania wiemy, że \(|AC|=4\sqrt{2}\). Ta przekątna kwadratu jest jednocześnie podstawią naszego trójkąta równobocznego \(ACS\), a więc wysokość obliczymy w następujący sposób:
$$H=\frac{a\sqrt{3}}{2} \\
H=\frac{4\sqrt{2}\cdot\sqrt{3}}{2} \\
H=\frac{4\sqrt{6}}{2} \\
H=2\sqrt{6}$$
Mamy już wszystkie potrzebne informacje, więc możemy podstawić dane i obliczyć objętość ostrosłupa.
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot16\cdot2\sqrt{6} \\
V=\frac{32\sqrt{6}}{3}$$
\(V=\frac{32\sqrt{6}}{3}\)

