W ostrosłupie prawidłowym czworokątnym ABCDS o podstawie ABCD i wierzchołku S trójkąt ACS jest równoboczny i ma bok długości 8

W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) i wierzchołku \(S\) trójkąt \(ACS\) jest równoboczny i ma bok długości \(8\). Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).

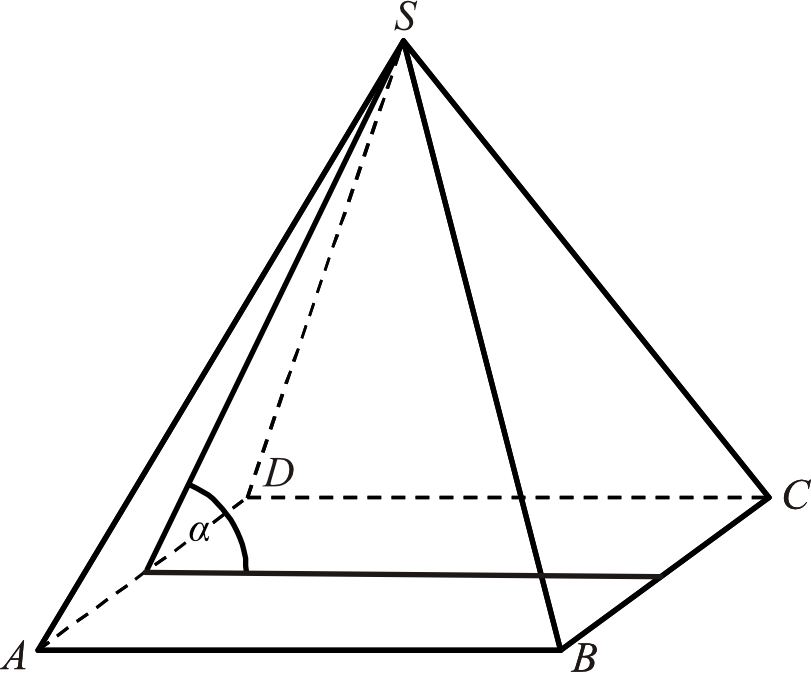
Dorysujmy sobie przekątną \(AC\), bo z treści zadania wynika, że będziemy pracować na trójkącie \(ACS\).

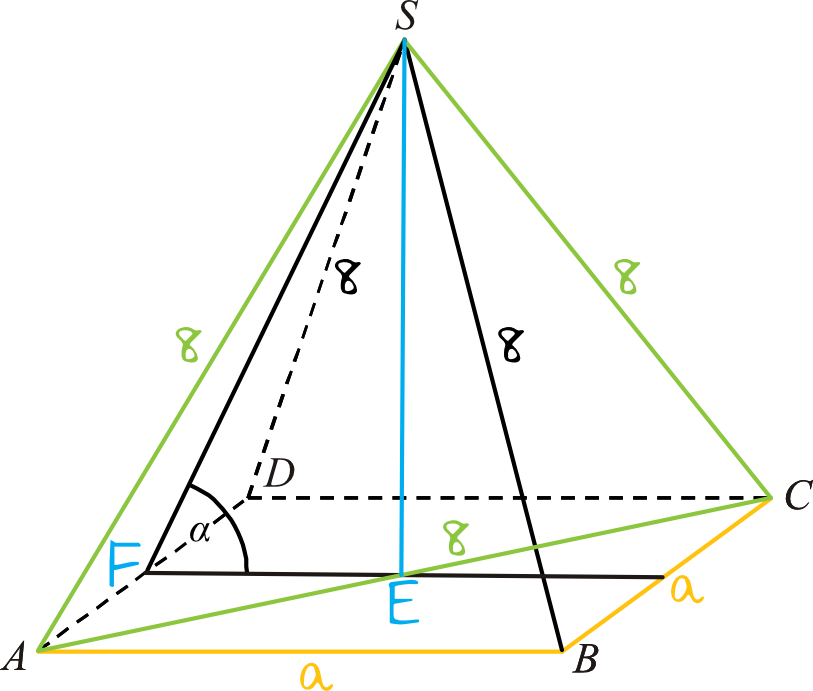
Warto zauważyć, że skoro \(ACS\) jest trójkątem równobocznym, to \(|AC|=|AS|=|SD|=8\).

Potrzebujemy obliczyć sinus kąta nachylenia ściany bocznej do podstawy, czyli zgodnie z naszym rysunkiem:
$$sinα=\frac{|SE|}{|SF|}$$

Skoro jest to ostrosłup prawidłowy czworokątny, to w swojej podstawie ma on na pewno kwadrat. My znamy długość przekątnej tego kwadratu, bo \(|AC|=8\). Z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\), zatem:
$$a\sqrt{2}=8 \\
a=\frac{8}{\sqrt{2}}=\frac{8\sqrt{2}}{2}=4\sqrt{2}$$

Skorzystamy tutaj ze standardowego wzoru na wysokość w trójkącie równobocznym, wiedząc że bok naszego trójkąta \(ACS\) ma długość \(a=8\).
$$|SE|=\frac{a\sqrt{3}}{2} \\
|SE|=\frac{8\sqrt{3}}{2} \\
|SE|=4\sqrt{3}$$

Spójrzmy na trójkąt \(FDS\). Jest to na pewno trójkąt prostokątny, bo wysokość ściany bocznej jest opuszczona pod kątem prostym. Punkt \(F\) znajduje się w połowie długości odcinka \(AD\), bo \(ADS\) jest trójkątem równoramiennym, a wysokość trójkąta równoramiennego dzieli podstawę na dwie równe części. Długość odcinka \(AD\) wyliczyliśmy w drugim kroku, a to oznacza, że:
$$|FD|=\frac{1}{2}\cdot4\sqrt{2} \\
|FD|=2\sqrt{2}$$

Skoro znamy długość \(|FD|=2\sqrt{2}\), wiemy też, że \(|SD|=8\), to z Twierdzenia Pitagorasa obliczymy potrzebną nam długość \(|SF|\):
$$|FD|^2+|SF|^2=|SD|^2 \\
(2\sqrt{2})^2+|SF|^2=8^2 \\
4\cdot2+|SF|^2=64 \\
8+|SF|^2=64 \\
|SF|^2=56 \\
|SF|=\sqrt{56}=\sqrt{4\cdot14}=2\sqrt{14}$$

Wszystkie potrzebne długości już wyznaczyliśmy, zatem wystarczy je tylko podstawić do wzoru który zapisaliśmy sobie w pierwszym kroku.
$$sinα=\frac{|SE|}{|SF|} \\
sinα=\frac{4\sqrt{3}}{2\sqrt{14}} \\
sinα=\frac{4\sqrt{3}\cdot\sqrt{14}}{2\sqrt{14}\cdot\sqrt{14}} \\
sinα=\frac{4\sqrt{3}\cdot\sqrt{14}}{2\sqrt{14}\cdot\sqrt{14}} \\
sinα=\frac{4\sqrt{42}}{2\cdot14} \\
sinα=\frac{4\sqrt{42}}{28} \\
sinα=\frac{\sqrt{42}}{7}$$

\(sinα=\frac{\sqrt{42}}{7}\)