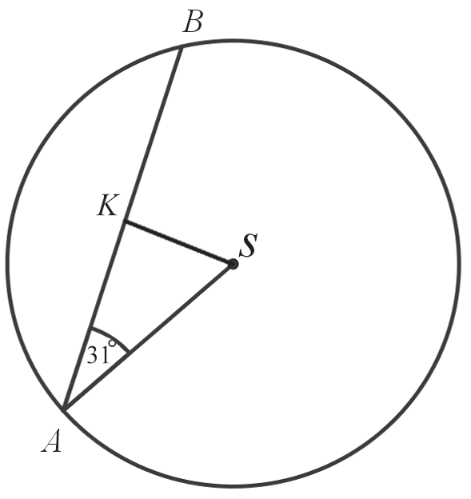
W okręgu o środku w punkcie \(S\) poprowadzono cięciwę \(AB\), która utworzyła z promieniem \(AS\) kąt o mierze \(31°\) (zobacz rysunek). Promień tego okręgu ma długość \(10\). Odległość punktu \(S\) od cięciwy \(AB\) jest liczbą z przedziału:
\(\langle\frac{9}{2};\frac{11}{2}\rangle\)
\(\langle\frac{11}{2};\frac{13}{2}\rangle\)
\(\langle\frac{13}{2};\frac{19}{2}\rangle\)
\(\langle\frac{19}{2};\frac{37}{2}\rangle\)
Rozwiązanie:
Skorzystamy tutaj z funkcji trygonometrycznych, a konkretnie z sinusa. Relacje między poszczególnymi odcinkami i kątami możemy zapisać jako:
$$sin31°=\frac{|KS|}{|AS|} \\
0,52\approx\frac{|KS|}{10} \\
|KS|\approx5,2$$
Jedynym przedziałem, w którym mieści się nasz wynik jest ten z pierwszej odpowiedzi, którego dolną granicą jest \(\frac{9}{2}=4,5\), a górną \(\frac{11}{2}=5,5\).
Odpowiedź:
A. \(\langle\frac{9}{2};\frac{11}{2}\rangle\)

