W okręgu o środku \(O\) dany jest kąt o mierze \(50°\), zaznaczony na rysunku.
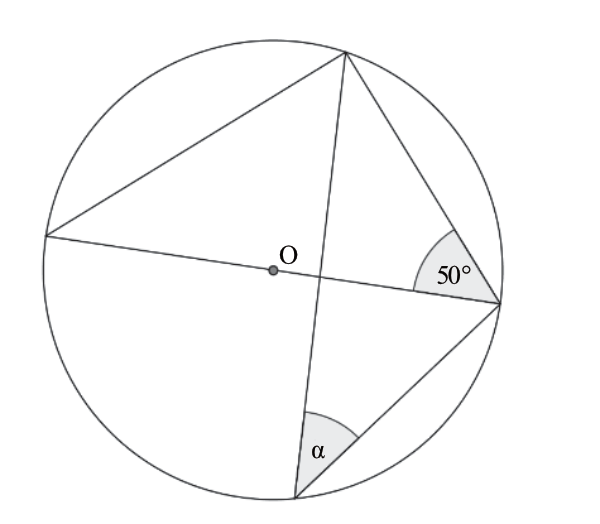
Miara kąta oznaczonego na rysunku literą \(α\) jest równa:
\(40°\)
\(50°\)
\(20°\)
\(25°\)
Rozwiązanie:
Wprowadźmy sobie pewne oznaczenia niektórych punktów, tak aby łatwiej było omówić zadanie:
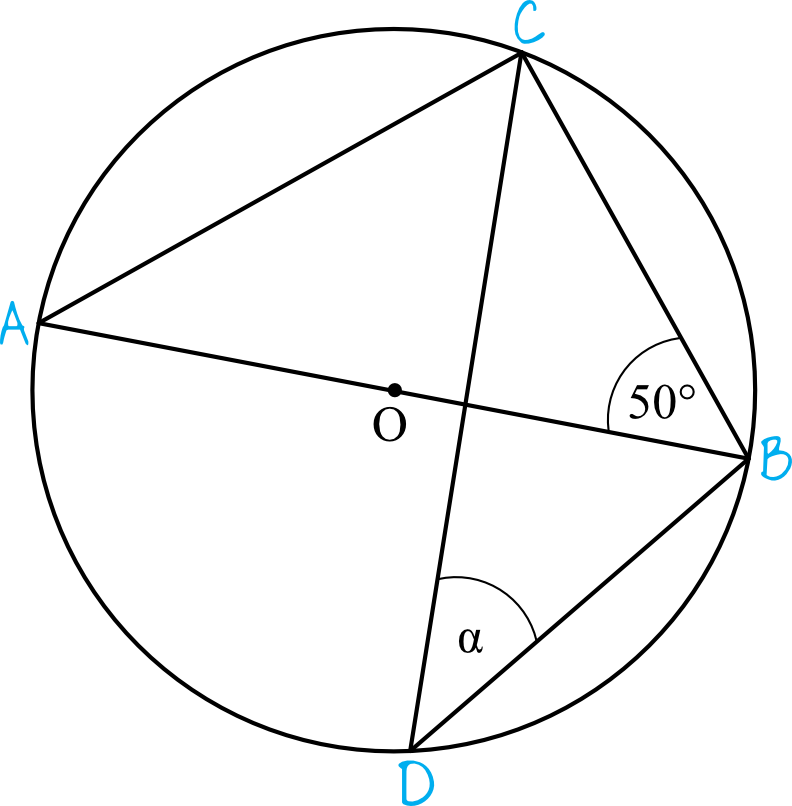
Przyjrzyjmy się na początek trójkątowi \(ABC\). Jest on na pewno prostokątny, bo jest oparty na średnicy okręgu. To z kolei oznacza, że kąt \(CAB\) będzie miał miarę równą:
$$|\sphericalangle CAB|=180°-90°-50°=40°$$
Kąt \(CDB\) zaznaczony na rysunku literą \(α\) jest oparty na tym samym co obliczony przed chwilą kąt \(CAB\). To oznacza, że ich miary muszą być sobie równe. Tak więc:
$$|\sphericalangle CDB|=|\sphericalangle CAB|=40°$$
Odpowiedź:
A. \(40°\)

