Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować ten graniastosłup, oznaczając na nim dane z treści zadania.
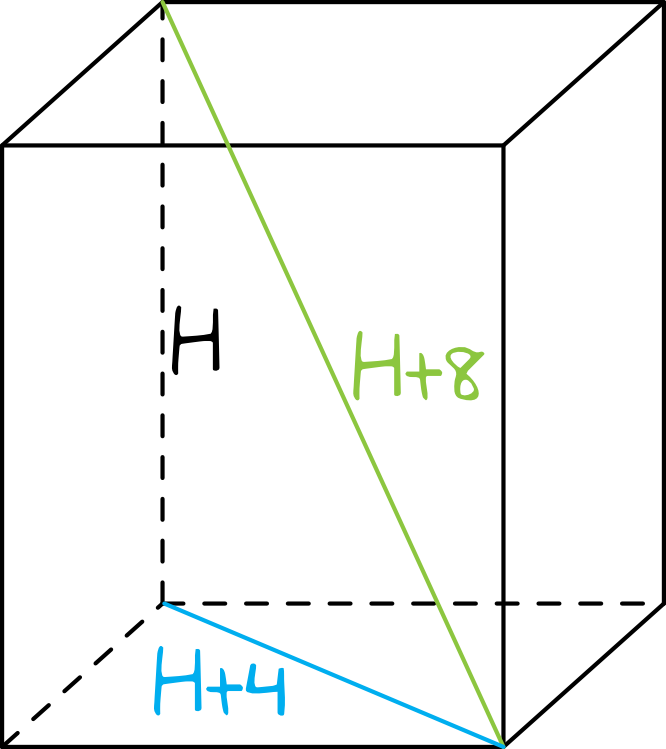
Krok 2. Zapisanie i rozwiązanie równania.
Z kluczowych odcinków powstał nam trójkąt prostokątny, dzięki czemu będziemy w stanie skorzystać z Twierdzenia Pitagorasa. Możemy zatem zapisać, że:
$$(H+4)^2+H^2=(H+8)^2 \\
H^2+8H+16+H^2=H^2+16H+64 \\
2H^2+8H+16=H^2+16H+64 \\
H^2-8H-48=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=1,\;b=-8,\;c=-48\)
$$Δ=b^2-4ac=(-8)^2-4\cdot1\cdot(-48)=64-(-192)=64+192=256 \\
\sqrt{Δ}=\sqrt{256}=16$$
$$H_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-8)-16}{2\cdot1}=\frac{8-16}{2}=\frac{-8}{2}=-4 \\
H_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-8)+16}{2\cdot1}=\frac{8+16}{2}=\frac{24}{2}=12$$
Wartość ujemną oczywiście odrzucamy, bo wysokość nie może być ujemna, zatem zostaje nam \(H=12\).
Krok 4. Obliczenie wartości sinusa.
Zgodnie z naszym rysunkiem oraz zgodnie możemy zapisać, że:
$$sinα=\frac{H}{H+8} \\
sinα=\frac{12}{12+8} \\
sinα=\frac{12}{20} \\
sinα=\frac{3}{5}$$