Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Na początek nanieśmy na rysunek dane z treści zadania i przy okazji wykonajmy jeden z celów tego zadania, czyli zaznaczmy poszukiwaną figurę:
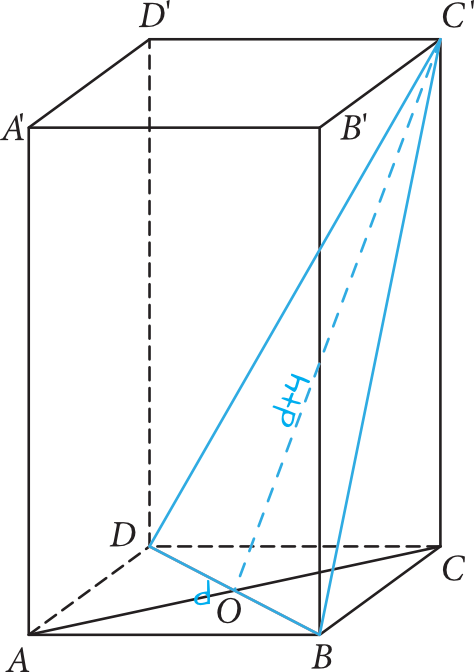
Krok 2. Obliczenie długości odcinka \(BD\).
Odcinek \(BD\) jest podstawą naszego trójkąta, który znalazł się w przekroju. Jeżeli oznaczymy sobie tę długość jako \(d\), to z treści zadania wynika, że wysokość tego trójkąta \(OC'\) ma długość \(d+4\). Skoro pole trójkąta jest równe \(48\), to otrzymamy następujące równanie:
$$P=\frac{1}{2}ah \\
48=\frac{1}{2}\cdot d\cdot(d+4) \\
48=\frac{1}{2}d^2+2d \quad\bigg/\cdot2 \\
96=d^2+4d \\
d^2+4d-96=0$$
Powstało nam równanie kwadratowe w postaci ogólnej, które możemy rozwiązać obliczając klasyczną deltę:
Współczynniki: \(a=1,\;b=4,\;c=-96\)
$$Δ=b^2-4ac=4^2-4\cdot1\cdot(-96)=16-(-384)=16+384=400 \\
\sqrt{Δ}=\sqrt{400}=20$$
$$d_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-4-20}{2\cdot1}=\frac{-24}{2}=-12 \\
d_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-4+20}{2\cdot1}=\frac{16}{2}=8$$
Otrzymaliśmy dwie możliwości, ale ujemny wynik musimy odrzucić, bo długość przekątnej podstawy musi być liczbą dodatnią. W związku z tym \(d=8\).
Krok 3. Obliczenie wysokości graniastosłupa.
Spójrzmy na trójkąt prostokątny \(OCC'\). Dolna podstawa będzie miała długość połowy przekątnej (którą przed chwilą wyznaczyliśmy). Możemy nawet zapisać, że:
$$|OC|=\frac{1}{2}d \\
|OC|=\frac{1}{2}\cdot8 \\
|OC|=4$$
Praktycznie znamy też długość przeciwprostokątnej tego trójkąta, bo z treści zadania wynika, że jest ona o \(4\) dłuższa od przekątnej podstawy, zatem:
$$|OC'|=d+4 \\
|OC'|=8+4 \\
|OC'|=12$$
Znając miary dwóch boków trójkąta \(OCC'\) możemy korzystając z Twierdzenia Pitagorasa obliczyć długość trzeciego boku, który jest jednocześnie wysokością naszego graniastosłupa:
$$|OC|^2+H^2=|OC'|^2 \\
4^2+H^2=12^2 \\
16+H^2=144 \\
H^2=128 \\
H=\sqrt{128} \quad\lor\quad H=-\sqrt{128}$$
Wysokość nie może być oczywiście ujemna, zatem zostaje nam \(H=\sqrt{128}\), co możemy jeszcze rozpisać jako \(H=\sqrt{64\cdot2}=8\sqrt{2}\).
Krok 4. Obliczenie długości krawędzi podstawy.
Wiemy już, że w podstawie znajduje się kwadrat o przekątnej długości \(d=8\). Z własności kwadratów wynika, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\), zatem:
$$a\sqrt{2}=8 \\
a=\frac{8}{\sqrt{2}} \\
a=\frac{8\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a=\frac{8\sqrt{2}}{2} \\
a=4\sqrt{2}$$
Krok 5. Obliczenie objętości graniastosłupa.
W podstawie graniastosłupa znajduje się kwadrat o boku \(a=4\sqrt{2}\), wiemy też że wysokość bryły jest równa \(H=8\sqrt{2}\), zatem:
$$V=P_{p}\cdot H \\
V=a^2\cdot H \\
V=(4\sqrt{2})^2\cdot8\sqrt{2} \\
V=16\cdot2\cdot8\sqrt{2} \\
V=256\sqrt{2}$$