Rozwiązanie
Krok 1. Obliczenie pola podstawy.
Graniastosłup jest prawidłowy, więc w podstawie musi znaleźć się figura foremna, a skoro jest to graniastosłup czworokątny, to w podstawie będziemy mieć kwadrat. Wiemy, że bok kwadratu ma długość \(a\), zatem:
$$P_{p}=a^2$$
Krok 2. Obliczenie pola powierzchni bocznej.
Wiemy, że pole powierzchni bocznej jest \(8\) razy większe od pola podstawy, zatem:
$$P_{b}=8a^2$$
Krok 3. Obliczenie wysokości graniastosłupa.
W graniastosłupie mamy cztery prostokątne ściany. Wiemy, że pole powierzchni bocznej (czyli pole wszystkich ścian bocznych) jest równe \(8a^2\). To oznacza, że pojedyncza ściana będzie mieć powierzchnię:
$$P_{śb}=8a^2:4 \\
P_{śb}=2a^2$$
Pojedyncza ściana boczna jest prostokątem w którym jeden bok jest taki jak krawędź podstawy, czyli ma długość \(a\), a drugi bok jest wysokością graniastosłupa.
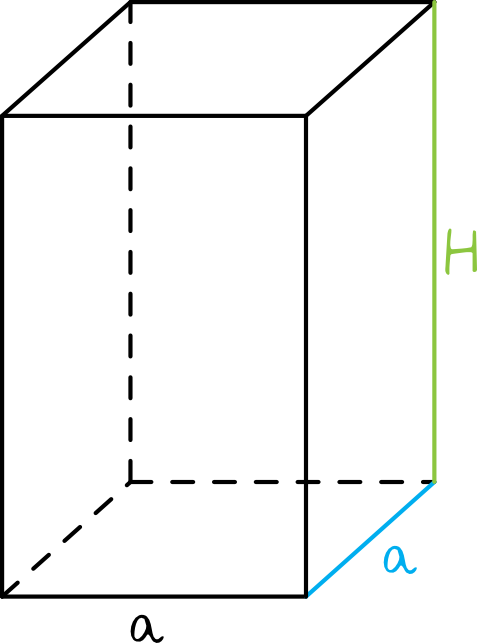
Skoro pole pojedynczej ściany ściany bocznej ma wynosić \(2a^2\), to:
$$P_{śb}=a\cdot H \\
2a^2=a\cdot H \\
H=2a$$
Krok 4. Obliczenie objętości.
Podstawiając do wzoru na objętość graniastosłupa znane nam dane otrzymamy:
$$V=P_{p}\cdot H \\
V=a^2\cdot2a \\
V=2a^3$$