Rozwiązanie
Krok 1. Ustalenie wartości kąta \(AMB\) oraz \(AOB\).
Kąt \(AMB\) oraz kąt wklęsły \(AOB\) oznaczony jako \(α\) są kątami opartymi na tym samym łuku. Zgodnie z własnościami kątów środkowych i wpisanych wiemy, że w takiej sytuacji kąt wpisany jest dwukrotnie mniejszy od kąta środkowego, czyli:
$$|\sphericalangle AMB|=\frac{1}{2}α$$
Krok 2. Sporządzenie rysunku pomocniczego.
Z treści zadania wynika, że kąt wewnętrzny \(AOB\) ma miarę taką samą co kąt \(AMB\), zatem możemy stworzyć następujący rysunek:
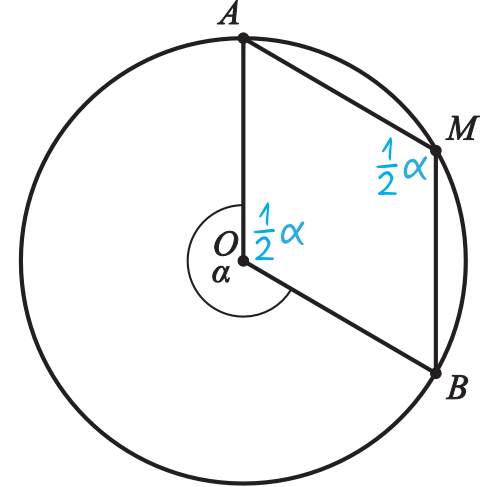
Krok 3. Obliczenie miary kąta \(α\).
Z rysunku wyraźnie widać, że kąt pełny jest równy \(1\frac{1}{2}α\), zatem:
$$1\frac{1}{2}α=360° \\
α=240°$$