Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
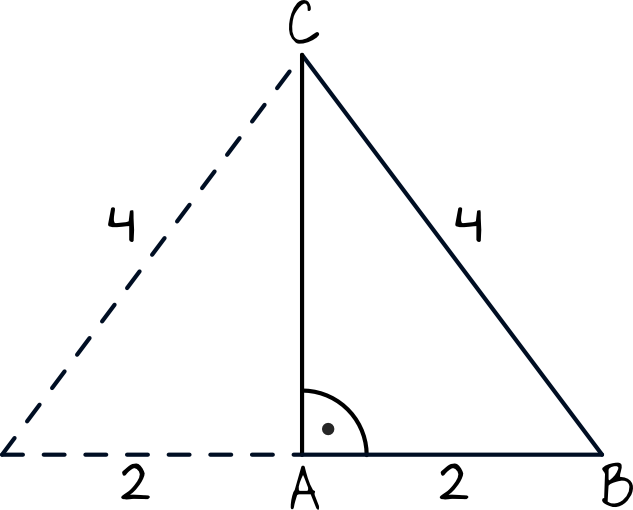
Spójrzmy na trójkąt \(ABC\). Wiedząc, że przyprostokątna \(AB\) jest połową przeciwprostokątnej \(BC\) możemy wywnioskować, że nasz trójkąt \(ABC\) jest połową trójkąta równobocznego. W trójkącie równobocznym wszystkie kąty mają miarę \(60°\), zatem \(|\sphericalangle ABC|=60°\).
Krok 2. Wyznaczenie miar kątów \(ACB\) oraz \(KLM\) i zakończenie dowodzenia.
Skoro suma miar kątów w trójkącie jest równa \(180°\), to:
$$|\sphericalangle ACB|=180°-90°-60°=30° \\
|\sphericalangle KLM|=180°-90°-60°=30°$$
W ten sposób udało nam się udowodnić, że obydwa trójkąty mają jednakowe miary kątów (30°, 60°, 90°), zatem są one trójkątami podobnymi na podstawie cechy kąt-kąt-kąt.