Rozwiązanie
I sposób: Korzystając z Twierdzenia Pitagorasa:
Krok 1. Sporządzenie rysunku pomocniczego.
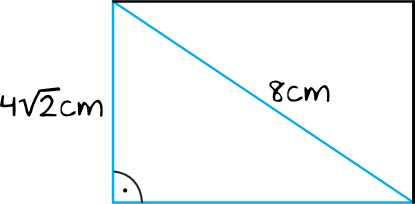
Krok 2. Obliczenie szerokości prostokąta.
Jeżeli uda nam się udowodnić, że bok o nieznanej nam długości \(b\) ma taką samą miarę co bok o długości \(a=4\sqrt{2}\), to będziemy mogli z całą pewnością stwierdzić, że ten prostokąt jest kwadratem. W tym celu skorzystamy po prostu z Twierdzenia Pitagorasa:
$$a^2+b^2=c^2 \\
(4\sqrt{2})^2+b^2=8^2 \\
16\cdot2+b^2=64 \\
32+b^2=64 \\
b^2=32 \\
b=\sqrt{32}=\sqrt{16\cdot2}=4\sqrt{2}$$
Krok 3. Zakończenie dowodzenia.
Udało nam się wykazać, że boki oznaczone jako \(a\) oraz \(b\) mają identyczną miarę, zatem ten prostokąt jest kwadratem.
II sposób: Korzystając z własności przekątnych kwadratu.
Z własności kwadratów wynika, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). Jeżeli więc pokażemy, że w przypadku tego prostokąta zachodzi taka zależność, to będziemy mogli stwierdzić, że faktycznie jest on kwadratem.
W związku z tym skoro \(a=4\sqrt{2}\) to przekątna kwadratu powinna mieć długość:
$$a\sqrt{2}=4\sqrt{2}\cdot\sqrt{2}=4\cdot2=8$$
Otrzymany wynik jest dokładnie taki sam jak długość przekątnej podanej w treści zadania, zatem możemy z całą pewnością stwierdzić, iż ten prostokąt jest kwadratem.