Tworząca stożka ma długość \(17\), a wysokość stożka jest krótsza od średnicy jego podstawy o \(22\). Oblicz pole powierzchni całkowitej i objętość tego stożka.
Narysujmy sobie przekrój stożka i zaznaczmy na nim odpowiednie miary i oznaczenia:
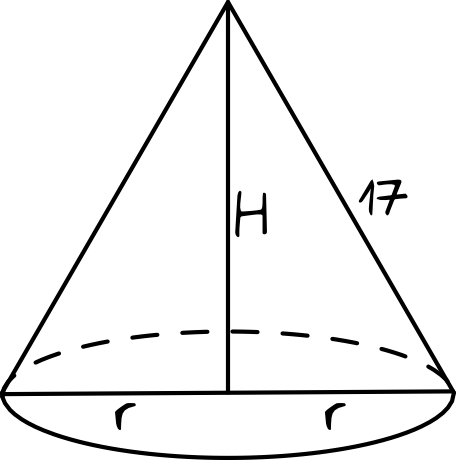
Warto sobie od razu zapisać, że zgodnie z treścią zadania wysokość stożka jest krótsza o \(22\) od średnicy podstawy (średnicy, nie promienia!). Zatem:
$$H=2r-22$$
Możemy skorzystać z Twierdzenia Pitagorasa, podstawiając za wysokość \(H=2r-22\). Otrzymamy wtedy:
$$r^2+H^2=17^2 \\
r^2+(2r-22)^2=289 \\
r^2+4r^2-88r+484=289 \\
5r^2-88r+195=0$$
Współczynniki: \(a=5,\;b=-88,\;c=195\)
$$Δ=b^2-4ac=(-88)^2-4\cdot5\cdot195=7744-3900=3844 \\
\sqrt{Δ}=\sqrt{3844}=62$$
$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-88)-62}{2\cdot5}=\frac{88-62}{10}=\frac{26}{10}=2,6 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-88)+62}{2\cdot5}=\frac{88+62}{10}=\frac{150}{10}=15$$
Obydwa rozwiązania są póki co dobre, żadnego z nich nie możemy odrzucić (odrzucilibyśmy np. wtedy, gdyby któraś z wartości wyszła ujemna).
Jeśli \(r_{1}=2,6\), to \(H_{1}=2\cdot2,6-22=5,2-22=-16,8\)
Jeśli \(r_{2}=15\), to \(H_{2}=2\cdot15-22=30-22=8\)
W przypadku pierwszej pary wyszła nam ujemna wysokość, więc odrzucamy całe to rozwiązanie. To oznacza, że jest tylko jedna para liczb, która spełnia warunki naszego zadania: \(r=15\) oraz \(H=8\).
Znając promień podstawy i wysokość stożka możemy już bez problemu obliczyć jego objętość:
$$V=\frac{1}{3}πr^2 H \\
V=\frac{1}{3}\cdot15^2\cdot8π \\
V=\frac{1}{3}\cdot225\cdot8π \\
V=\frac{1}{3}\cdot1800π \\
V=600π$$
Zgodnie z treścią zadania musimy jeszcze obliczyć pole powierzchni całkowitej.
$$P_{c}=πr\cdot(r+l) \\
P_{c}=π\cdot15\cdot(15+17) \\
P_{c}=π\cdot15\cdot32 \\
P_{c}=480π$$
\(P_{c}=480π\) oraz \(V=600π\)

