Tworząca stożka jest o 2 dłuższa od promienia jego podstawy, a pole powierzchni bocznej

Krok 1. Sporządzenie rysunku pomocniczego.
Z treści zadania wynika, że mamy taką oto sytuację:


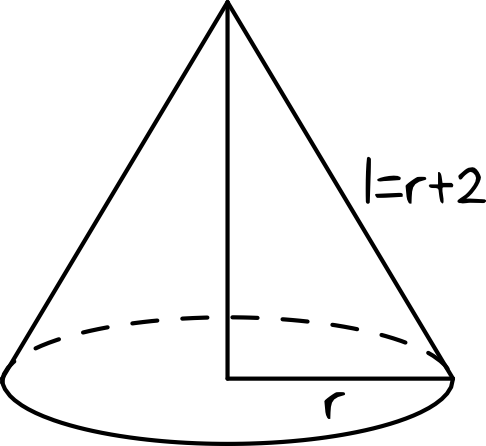
Krok 2. Obliczenie długości promienia podstawy.
Pole powierzchni bocznej możemy wyliczyć ze wzoru \(P_{b}=\pi rl\). Pole podstawy wyliczamy ze wzoru \(P=\pi r^2\). Wiemy, że pole powierzchni bocznej jest o \(2\pi\) większe od pola podstawy, zatem:
$$P_{b}=P_{p}+2\pi \\
\pi rl=\pi r^2+2\pi \quad\bigg/:\pi \\
rl=r^2+2$$

Wiemy, że \(l=r+2\), zatem:
$$r\cdot(r+2)=r^2+2 \\
r^2+2r=r^2+2 \\
2r=2 \\
r=1$$