Twierdzenie Pitagorasa to jedno z najważniejszych twierdzeń na matematyce, dlatego rozpracujmy je sobie bardzo dokładnie, zobaczmy na czym to twierdzenie polega oraz dowiedzmy się jak je wykorzystać w praktyce podczas rozwiązywania zadań z geometrii.
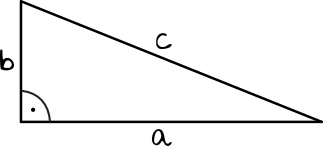
Okazuje się, że między suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej, co możemy opisać wzorem:
$$a^2+b^2=c^2$$
Kolejną bardzo ważną informacją jest fakt, że w tym wzorze pod \(a\) oraz \(b\) możemy podstawiać tylko i wyłącznie długości przyprostokątnych (czyli boków leżących przy kącie prostym). Bok \(c\) jest zarezerwowany dla przeciwprostokątnej. Nie możemy więc dowolnie podstawiać danych do wzoru, musimy trzymać się tych powyższych reguł.
Spróbujmy wykorzystać tę wiedzę w praktyce. Załóżmy, że znamy długości obydwu przyprostokątnych i są to \(a=3\) oraz \(b=4\). Chcemy policzyć długość przeciwprostokątnej, czyli długość boku \(c\). W tym właśnie pomoże nam Twierdzenie Pitagorasa do którego musimy podstawić znane nam miary:
$$a^2+b^2=c^2 \\
3^2+4^2=c^2 \\
9+16=c^2 \\
c^2=25 \\
c=5$$
W ten oto sposób udało nam się wyznaczyć długość przeciwprostokątnej trójkąta. Oczywiście twierdzenie jest na tyle uniwersalne, że równie dobrze dałoby się obliczyć długość jednej z przyprostokątnych, znając dwie pozostałe długości boków. Załóżmy, że tym razem wiemy o tym, że bok \(b=4\) oraz \(c=5\) i proszą nas o podanie długości trzeciego boku. Całość obliczeń będzie więc wyglądać następująco:
$$a^2+b^2=c^2 \\
a^2+4^2=5^2 \\
a^2+16=25 \\
a^2=9 \\
a=3$$
Można więc powiedzieć, że Twierdzenie Pitagorasa otwiera nam drogę do rozwiązania całej masy zadań z geometrii. Skoro mając dwie dowolne długości boków jesteśmy w stanie obliczyć długość trzeciego boku, to znaczy że będziemy w stanie obliczyć obwód lub pole takiej figury. Spójrzmy na poniższe przykłady:
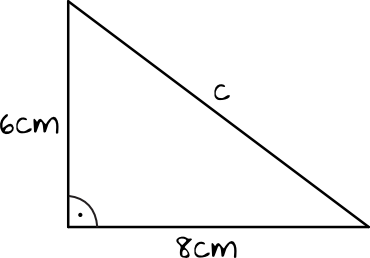
Do obliczenia obwodu trójkąta brakuje nam oczywiście długości trzeciego boku, czyli przeciwprostokątnej. Skorzystamy zatem z Twierdzenia Pitagorasa:
$$a^2+b^2=c^2 \\
6^2+8^2=c^2 \\
36+64=c^2 \\
c^2=100 \\
c=10[cm]$$
Znając długości wszystkich boków możemy przystąpić do obliczenia obwodu:
$$Obw: 6cm+8cm+10cm=24cm$$
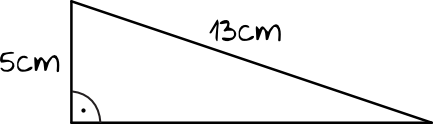
W trójkącie prostokątnym jedna przyprostokątna jest jednocześnie długością podstawy trójkąta, a druga przyprostokątna jest jego wysokością. Jeśli więc poznamy długość obydwu przyprostokątnych, to bez problemu obliczymy pole trójkąta. Jedną przyprostokątną już znamy \(a=5cm\). Drugą policzymy z Twierdzenia Pitagorasa:
$$a^2+b^2=c^2 \\
5^2+b^2=13^2 \\
25+b^2=169 \\
b^2=144 \\
b=\sqrt{144}=12[cm]$$
Pole trójkąta będzie zatem równe:
$$P=\frac{5cm\cdot12cm}{2}=\frac{60cm^2}{2}=30cm^2$$
Na początku musimy ustalić długości obydwu przyprostokątnych:
$$a=3cm \\
b=2\cdot3cm=6cm$$
Szukamy długości przeciwprostokątnej, zatem ponownie skorzystamy z Twierdzenia Pitagorasa.
$$a^2+b^2=c^2 \\
3^2+6^2=c^2 \\
9+36=c^2 \\
c^2=45 \\
c=\sqrt{45}$$
Tym razem długość przeciwprostokątnej musimy zostawić w postaci pierwiastka, bo nie uda nam się w żaden sposób zapisać tego sensowniej.
Choć Twierdzenie Pitagorasa dotyczy tylko i wyłącznie trójkątów prostokątnych, to czasem takie trójkąty uda nam się wyodrębnić w pozostałych figurach geometrycznych.
W tym zadaniu na pewno przyda się rysunek, nawet taki szkicowy:
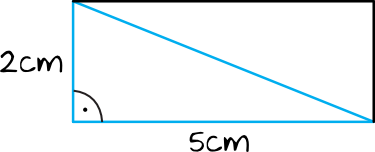
Widzimy wyraźnie, że w takim prostokącie możemy wyodrębnić trójkąt prostokątny, którego przyprostokątnymi są boki prostokąta, a przeciwprostokątną jest poszukiwana przez nas przekątna. To by oznaczało, że tutaj także możemy skorzystać z Twierdzenia Pitagorasa. Zapiszmy zatem:
$$a^2+b^2=c^2 \\
2^2+5^2=c^2 \\
4+25=c^2 \\
c^2=29 \\
c=\sqrt{29}$$
Tutaj ponownie otrzymany wynik jest przedstawiony w najlepszej możliwej formie, dlatego ostateczną odpowiedzią jest to, że przekątna prostokąta ma długość \(\sqrt{29}\).

to samo co w podręczniku ale bardziej objaśnione, dzięki