Twierdzenie cosinusów jest wykorzystywane do obliczenia długości jednego boku dowolnego trójkąta (nie musi to być trójkąt prostokątny) kiedy znamy długości dwóch pozostałych boków oraz kąt znajdujący się między tymi znanymi bokami.
Twierdzenie cosinusów
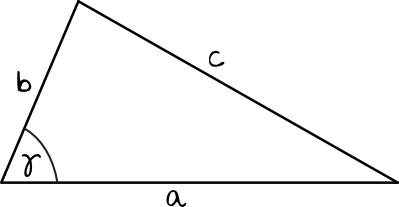
$$c^2=a^2+b^2-2ab\cosγ$$

$$c^2=a^2+b^2-2ab\cosγ$$
\(a, b\) – znane długości boków
\(c\) – szukana długość boku
\(γ\) – kąt między bokami o znanych długościach
Spójrzmy jak wygląda przykładowe zadanie z wykorzystaniem twierdzenia cosinusów.
Przykład 1. Oblicz długość boku \(c\).
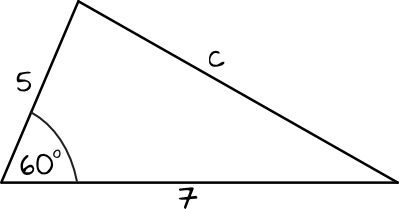

Znamy długości boków \(a\) i \(b\), wiemy też że \(cos60°=0,5\), więc nie pozostaje nam nic innego jak podstawić te dane do twierdzenia cosinusów i policzyć długość boku \(c\):
$$c^2=5^2+7^2-2\cdot5\cdot7\cdot cos60° \\
c^2=25+49-70\cdot0,5 \\
c^2=74-35 \\
c^2=39 \\
c=\sqrt{39}$$
Długość boku \(c\) wynosi \(\sqrt{39}\)
Pamiętaj! Twierdzenie cosinusów działa dla wszystkich trójkątów, nie tylko tych prostokątnych! To jest przewaga tego twierdzenia nad Twierdzeniem Pitagorasa, które dotyczy tylko trójkątów prostokątnych.
Zobacz też: Twierdzenie sinusów
