Trygonometria w stereometrii - zadania
Zadanie 1. (4pkt) Podstawą ostrosłupa \(ABCDS\) jest romb \(ABCD\) o boku długości \(4\). Kąt \(ABC\) rombu ma miarę \(120°\) oraz \(|AS|=|CS|=10\) i \(|BS|=|DS|\). Oblicz sinus kąta nachylenia krawędzi \(BS\) do płaszczyzny podstawy ostrosłupa.
Odpowiedź
\(sinα=\sqrt{\frac{22}{23}}\)
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Stwórzmy sobie szkic rysunku na którym zaznaczymy wszystkie informacje z treści zadania.
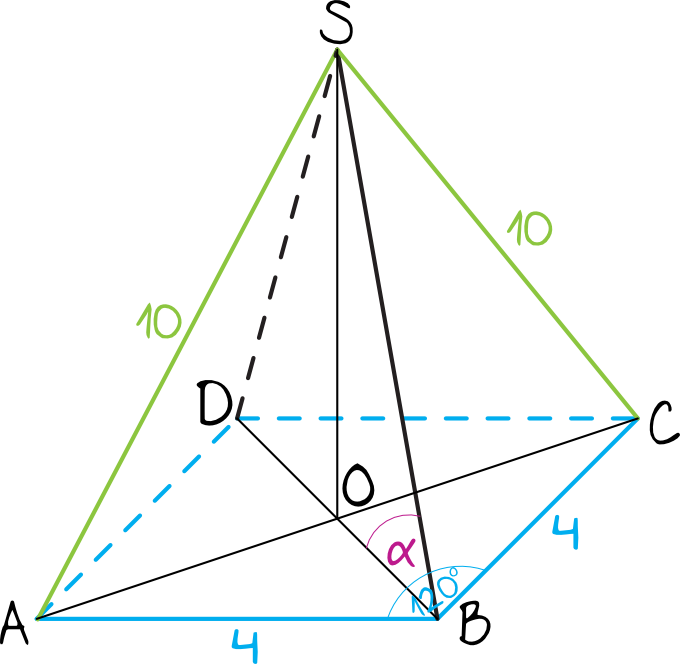
Krok 2. Obliczenie długości odcinków \(CO\) oraz \(BO\).
Wbrew pozorom nie będą to odcinki równej długości, bo przecież przekątne rombu mają różne długości.
Przekątne rombu dzielą kąty przy wierzchołkach na dwie równe części. To oznacza, że kąty \(CBD\) oraz \(CDB\) mają po \(60°\). To z kolei powoduje, że trójkąt \(BCD\) jest trójkątem równobocznym o boku długości \(4\). Analogicznie będzie z trójkątem \(ABD\). Wszystko wyjaśni poniższy rysunek z zaznaczonymi kątami i z niebieskimi liniami, które mówią nam o tym które tworzą dwa trójkąty równoboczne:
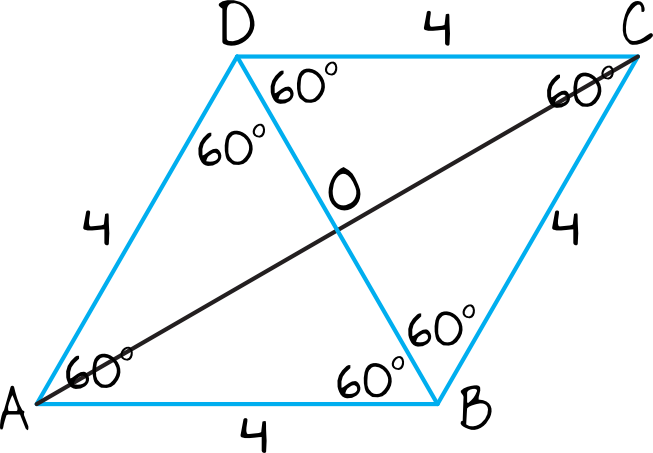
To dla nas bardzo ważna informacja, bo teraz bez przeszkód obliczymy długość odcinka \(CO\), który jest wysokością trójkąta równobocznego \(BCD\) o boku \(a=4\).
$$|CO|=\frac{a\sqrt{3}}{2}=\frac{4\sqrt{3}}{2}=2\sqrt{3}$$
Skoro ustaliliśmy sobie, że trójkąt \(BCD\) jest równoboczny, to znaczy że przekątna \(BD\) ma także długość \(4\). Przekątne w rombie przecinają się w połowie swojej długości, a to pozwoli nam na obliczenie długości boku \(BO\):
$$|BO|=4:2=2$$
Krok 3. Obliczenie długości odcinka \(SO\), czyli wysokości ostrosłupa.
W poprzednim kroku obliczyliśmy długość odcinka \(|CO|=2\sqrt{3}\). Z treści zadania znamy też długość krawędzi \(|SC|=10\). To oznacza, że bez przeszkód obliczymy wysokość \(SO\) naszego ostrosłupa korzystając z Twierdzenia Pitagorasa w trójkącie \(SOC\):
$$a^2+b^2=c^2 \\
|SO|^2+|CO|^2=|SC|^2 \\
|SO|^2+(2\sqrt{3})^2=10^2 \\
|SO|^2+4\cdot3=100 \\
|SO|^2+12=100 \\
|SO|^2=88 \\
|SO|=\sqrt{88} \quad\lor\quad |SO|=-\sqrt{88}$$
Wartość ujemną oczywiście odrzucamy, bo bok musi mieć dodatnią długość i jest ona równa \(|SO|=\sqrt{88}=2\sqrt{22}\).
Krok 4. Obliczenie długości odcinka \(BS\) (czyli naszej krawędzi bocznej).
Tu ponownie skorzystamy sobie z Twierdzenia Pitagorasa, tym razem wobec trójkąta \(BOS\). Znamy wysokości obu przyprostokątnych \(|BO|=2\) (wyliczyliśmy to w drugim kroku) oraz \(|SO|=2\sqrt{22}\) (wyliczyliśmy to w trzecim kroku), więc bez przeszkód wyznaczymy długość krawędzi \(BS\):
$$a^2+b^2=c^2 \\
|BO|^2+|SO|^2=|BS|^2 \\
2^2+(2\sqrt{22})^2=|BS|^2 \\
4+4\cdot22=|BS|^2 \\
|BS|^2=92 \\
|BS|=\sqrt{92} \quad\lor\quad |BS|=-\sqrt{92}$$
Wartość ujemną także oczywiście odrzucamy, więc zostaje nam \(|BS|=\sqrt{92}=2\sqrt{23}\).
Krok 5. Obliczenie wartości sinusa.
Znamy już wszystkie potrzebne miary, więc na koniec musimy obliczyć jeszcze sinus kąta nachylenia krawędzi \(BS\) do płaszczyzny podstawy ostrosłupa:
$$sinα=\frac{|SO|}{|BS|}=\frac{2\sqrt{22}}{2\sqrt{23}}=\frac{\sqrt{22}}{\sqrt{23}}=\sqrt{\frac{22}{23}}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długości odcinków \(|CO|=2\sqrt{3}\) oraz \(|BO|=2\) (patrz: Krok 2.).
2 pkt
• Gdy obliczysz wysokość ostrosłupa, czyli \(|SO|=\sqrt{88}=2\sqrt{22}\) (patrz: Krok 3.).
3 pkt
• Gdy obliczysz długość krawędzi bocznej ostrosłupa, czyli \(|BS|=\sqrt{92}=2\sqrt{23}\) (patrz: Krok 4.).
ALBO
• Gdy obliczysz tangens kąta nachylenia krótszej krawędzi bocznej ostrosłupa do płaszczyzny podstawy, czyli \(tgβ=\sqrt{22}\).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 2. (4pkt) W graniastosłupie prawidłowym czworokątnym \(ABCDEFGH\) przekątna \(AC\) podstawy ma długość \(4\). Kąt \(ACE\) jest równy \(60°\). Oblicz objętość ostrosłupa \(ABCDE\) przedstawionego na poniższym rysunku.
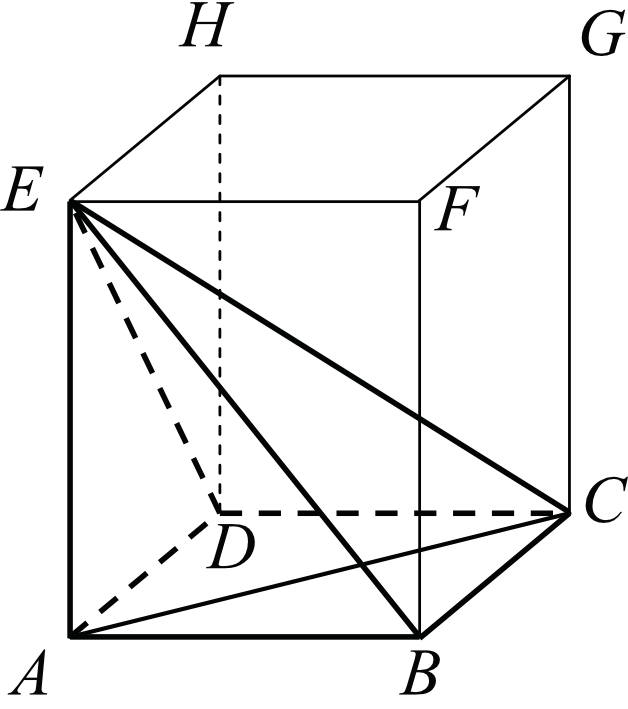
Odpowiedź
\(V=\frac{32\sqrt{3}}{3}\)
Wyjaśnienie:
Krok 1. Obliczenie wysokości graniastosłupa.
Skorzystamy tutaj z trójkąta prostokątnego \(ACE\). Znamy długość \(|AC|=4\) i znamy też miarę jednego z kątów \(|\sphericalangle ACE|=60°\). Te dwie dane posłużą nam do wyznaczenia wysokości graniastosłupa (czyli \(AE\)), a skorzystamy tutaj z funkcji tangensa:
$$tg60°=\frac{|AE|}{|AC|} \\
\sqrt{3}=\frac{|AE|}{4} \\
|AE|=4\sqrt{3}$$
Krok 2. Obliczenie długości krawędzi podstawy.
Skoro jest to graniastosłup prawidłowy czworokątny, to znaczy że w swojej podstawie ma on kwadrat. Znamy przekątną tego kwadratu i jest ona równa \(d=|AC|=4\). Z własności kwadratu wiemy też, że \(d=a\sqrt{2}\), a to pozwoli nam szybko wyliczyć długość krawędzi podstawy:
$$4=a\sqrt{2} \\
a=\frac{4}{\sqrt{2}}=\frac{4\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$$
Ta długość przyda nam się teraz do obliczenia pola podstawy.
Krok 3. Obliczenie pola podstawy.
Skoro w podstawie mamy kwadrat o boku \(a=2\sqrt{2}\), to pole podstawy będzie równe:
$$P_{p}=(2\sqrt{2})^2=4\cdot2=8$$
Krok 4. Obliczenie objętości wyznaczonego ostrosłupa.
Musimy teraz obliczyć objętość ostrosłupa. Znamy jego wysokość \(h=4\sqrt{3}\), obliczyliśmy także że \(P_{p}=8\), więc wystarczy już tylko podstawić te dane do standardowego wzoru na objętosć ostrosłupów:
$$V=\frac{1}{3}\cdot P_{p}\cdot H \\
V=\frac{1}{3}\cdot8\cdot4\sqrt{3} \\
V=\frac{32\sqrt{3}}{3}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 1.).
ALBO
• Gdy gdy obliczysz pole podstawy ostrosłupa (patrz: Krok 3.).
2 pkt
• Gdy obliczysz wysokość ostrosłupa oraz pole podstawy (patrz: Krok 1. oraz 3.), ale jedna z otrzymanych wartości będzie błędna w wyniku błędu rachunkowego.
3 pkt
• Gdy obliczysz poprawnie wysokość ostrosłupa oraz pole podstawy (patrz: Krok 1. oraz 3.).
ALBO
• Gdy obliczysz obliczysz objętość ostrosłupa zapominając o tym, że we wzorze jest mnożenie przez \(\frac{1}{3}\).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 3. (4pkt) Objętość ostrosłupa prawidłowego trójkątnego \(ABCS\) (tak jak na rysunku) jest równa \(72\), a promień okręgu wpisanego w podstawę \(ABC\) tego ostrosłupa jest równy \(2\). Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
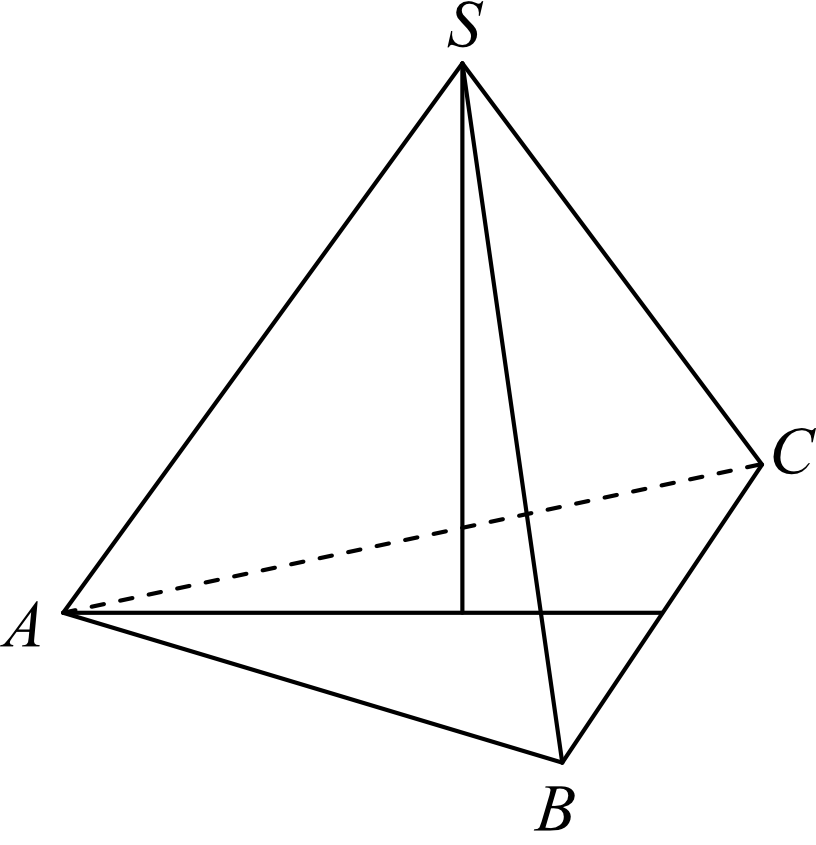
Odpowiedź
\(tgα=\frac{\sqrt{3}}{9}\)
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Dorysujmy sobie wysokość ściany bocznej, oznaczmy kąt którego tangensa musimy obliczyć. Przyjmijmy też, że krawędź podstawy jest równa \(a\):
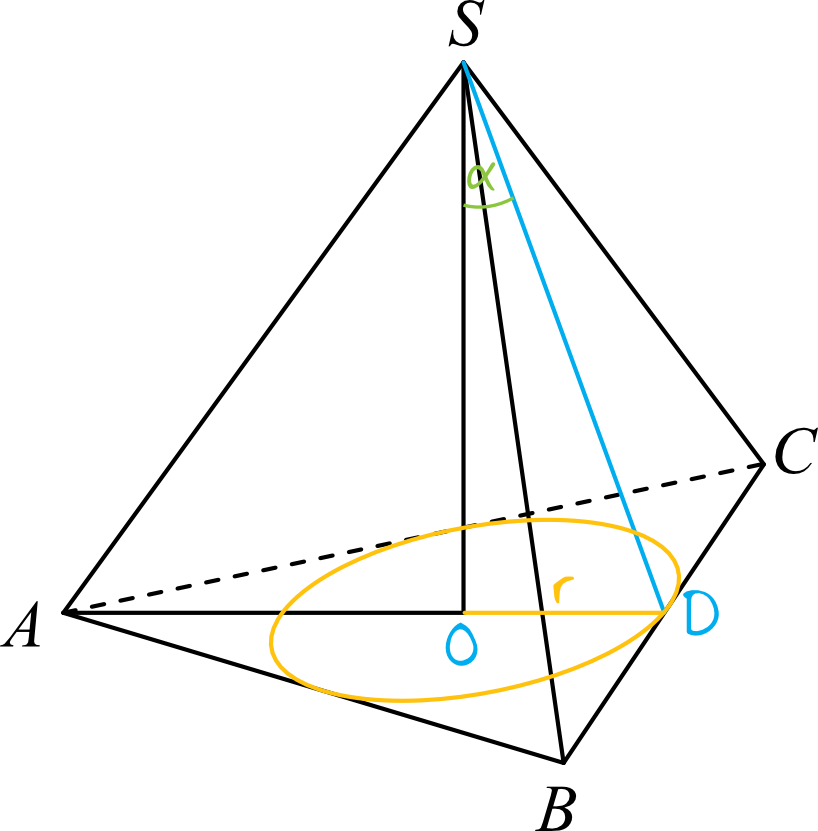
Musimy obliczyć tangens między wysokością ostrosłupa i jego ścianą boczną, czyli:
$$tgα=\frac{|OD|}{|SO|}$$
Długość odcinka \(OD\) jest nam znana, bo jest to długość promienia okręgu, czyli \(|OD|=r=2\). Potrzebujemy jeszcze wyznaczyć wysokość całego ostrosłupa i dopiero wtedy będziemy mogli obliczyć wartość tego tangensa.
Krok 2. Wyznaczenie długości krawędzi podstawy.
Aby wyznaczyć wysokość ostrosłupa musimy najpierw policzyć pole podstawy, bowiem znając pole podstawy i objętość bryły (a ta jest podana w treści zadania) bez problemu obliczymy poszukiwaną wysokość ostrosłupa. Do obliczenia pola podstawy brakuje nam tak naprawdę znajomości długości krawędzi trójkąta równobocznego, który znajduje się w podstawie i to właśnie tą długość teraz wyznaczymy (wiemy, że jest to trójkąt równoboczny, bo jest to ostrosłup prawidłowy trójkątny).
Punktem wyjścia będzie promień okręgu wpisanego w podstawę (którego długość znamy, bo \(r=2\)), który stanowi \(\frac{1}{3}\) wysokości tego trójkąta. Skoro jest to trójkąt równoboczny to wzór na jego wysokość możemy zapisać jako \(h=\frac{a\sqrt{3}}{2}\), zatem:
$$r=\frac{1}{3}\cdot h\\
r=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2} \\
2=\frac{a\sqrt{3}}{6} \\
a\sqrt{3}=12 \\
a=\frac{12}{\sqrt{3}}=\frac{12\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{12\sqrt{3}}{3}=4\sqrt{3}$$
Krok 3. Obliczenie pola podstawy.
Znając długość krawędzi możemy bez przeszkód obliczyć pole podstawy:
$$P_{p}=\frac{a^2\sqrt{3}}{4} \\
P_{p}=\frac{(4\sqrt{3})^2\sqrt{3}}{4} \\
P_{p}=\frac{16\cdot3\cdot\sqrt{3}}{4} \\
P_{p}=12\sqrt{3}$$
Krok 4. Obliczenie wysokości ostrosłupa.
Zgodnie z tym co opisaliśmy sobie wcześniej - wysokość ostrosłupa wyznaczymy ze wzoru na objętość:
$$V=\frac{1}{3}P_{p}\cdot H \\
72=\frac{1}{3}\cdot12\sqrt{3}\cdot H \\
72=4\sqrt{3}\cdot H \\
H=\frac{72}{4\sqrt{3}} \\
H=\frac{18}{\sqrt{3}}=\frac{18\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{18\sqrt{3}}{3}=6\sqrt{3}$$
Krok 5. Oblicznie wartości tangensa.
Znamy już wszystkie potrzebne miary, możemy więc wyznaczyć wartość tangensa między wysokością ostrosłupa i jego ścianą boczną:
$$|OD|=r=2 \\
|SO|=H=6\sqrt{3} \\
\text{więc} \\
tgα=\frac{|OD|}{|SO|} \\
tgα=\frac{2}{6\sqrt{3}}=\frac{2\cdot\sqrt{3}}{6\sqrt{3}\cdot\sqrt{3}}=\frac{2\sqrt{3}}{18}=\frac{\sqrt{3}}{9}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy na rysunku zaznaczysz kąt między wysokością ostrosłupa i jego ścianą boczną (patrz: Krok 1.).
2 pkt
• Gdy obliczysz długość boku trójkąta znajdującego się w podstawie (patrz: Krok 2.).
3 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 4.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 4. (4pkt) W ostrosłupie prawidłowym czworokątnym \(ABCDS\) (zobacz rysunek) przekątna \(AC\) podstawy ma długość \(4\sqrt{2}\). Kąt \(ASC\) między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę \(60°\). Oblicz objętość tego ostrosłupa.
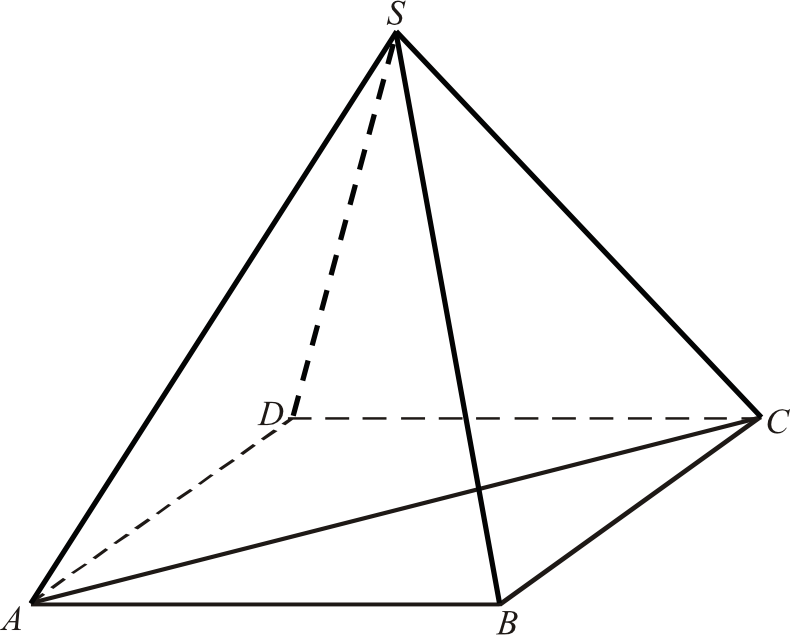
Odpowiedź
\(V=\frac{32\sqrt{6}}{3}\)
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego i analiza danych z treści zadania.
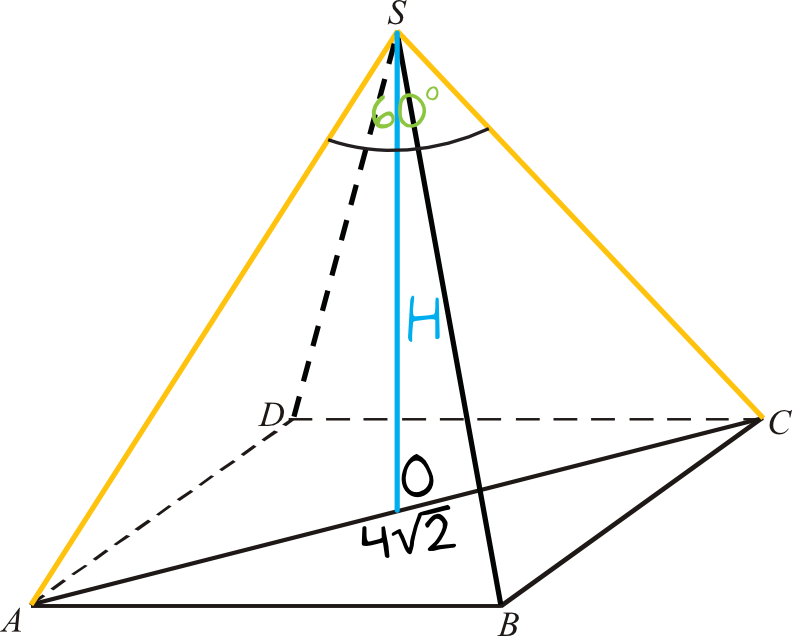
Dorysujmy sobie wysokość naszego ostrosłupa, bo będzie nam ona potrzebna do obliczenia objętości. Widzimy wyraźnie, że wysokość ostrosłupa jest jednocześnie wysokością trójkąta \(ACS\). Skoro jest to ostrosłup prawidłowy czworokątny, to wszystkie ramiona trójkąta \(ACS\) mają tą samą długość (patrz kolor pomarańczowy na rysunku), a więc na pewno jest to trójkąt równoramienny. Ale... okazuje się, że on jest nawet nie tyle równoramienny, co równoboczny. Skąd to wynika? Wiemy, że między pomarańczowymi ramionami kąt ma miarę \(60°\). To oznacza, że kąty przy podstawie muszą mieć łącznie \(180°-60°=120°\). W trójkącie równoramiennym kąty przy podstawie muszą mieć tą samą miarę, czyli każdy z nich ma\(120°:2=60°\). Z tego wynika, że wszystkie kąty trójkąta \(ACS\) będą mieć \(60°\).
Dostrzeżenie tej własności bardzo ułatwia nam rozwiązanie zadania, bo w tablicach mamy bezpośredni wzór na wysokość trójkąta równobocznego. Gdybyśmy nie zauważyli że to trójkąt równoboczny, to moglibyśmy próbować obliczyć wysokość z tangensa w trójkącie \(AOS\).
Krok 2. Obliczenie pola podstawy.
W podstawie mamy na pewno kwadrat, bo jest to ostrosłup prawidłowy czworokątny. Z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną równą \(a\sqrt{2}\). Długość tej przekątnej jest podana w treści i wynosi \(|AC|=4\sqrt{2}\), zatem w podstawie mamy kwadrat o boku \(4\). To oznacza, że jego pole będzie równe:
$$P_{p}=a^2 \\
P_{p}=4^2 \\
P_{p}=16$$
Krok 3. Obliczenie długości wysokości ostrosłupa.
Z treści zadania wiemy, że \(|AC|=4\sqrt{2}\). Ta przekątna kwadratu jest jednocześnie podstawią naszego trójkąta równobocznego \(ACS\), a więc wysokość obliczymy w następujący sposób:
$$H=\frac{a\sqrt{3}}{2} \\
H=\frac{4\sqrt{2}\cdot\sqrt{3}}{2} \\
H=\frac{4\sqrt{6}}{2} \\
H=2\sqrt{6}$$
Krok 4. Obliczenie objętości ostrosłupa.
Mamy już wszystkie potrzebne informacje, więc możemy podstawić dane i obliczyć objętość ostrosłupa.
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot16\cdot2\sqrt{6} \\
V=\frac{32\sqrt{6}}{3}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość krawędzi podstawy (patrz: Krok 2.)
2 pkt
• Gdy pole podstawy (patrz: Krok 2.).
3 pkt
• Gdy wyznaczysz wysokość ostrosłupa (patrz: Krok 3.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 5. (4pkt) Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość ściany bocznej tego ostrosłupa jest równa \(22\), a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy \(\frac{4\sqrt{6}}{5}\). Oblicz objętość tego ostrosłupa.
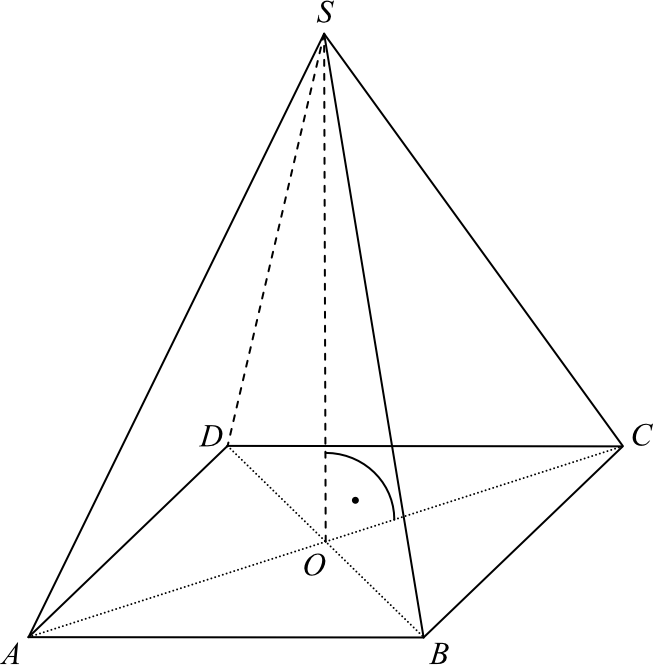
Odpowiedź
\(V=\frac{3200\sqrt{6}}{3}\)
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Zaznaczmy na rysunku z treści zadania odpowiednie długości, które zostały nam podane w treści. Skoro znamy tangens kąta nachylenia ściany bocznej, to także dorysujemy sobie wysokość naszej bocznej ściany.
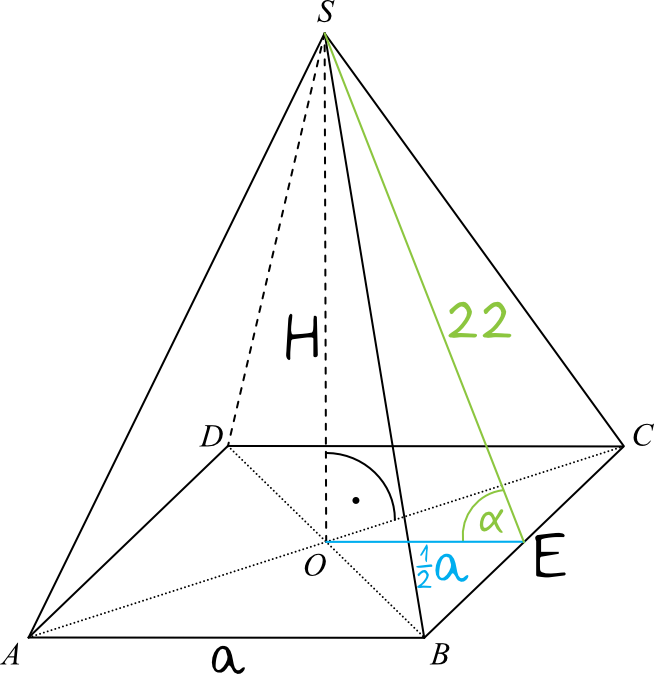
Już na podstawie tego rysunku warto zauważyć, że jeśli krawędź podstawy oznaczymy sobie jako \(a\), to odcinek \(|OE|=\frac{1}{2}a\).
Krok 2. Wyznaczenie wzoru na wysokość ostrosłupa.
Korzystając z tangensa spróbujmy wyznaczyć wzór na wysokość ostrosłupa.
$$tgα=\frac{|SO|}{|OE|} \\
\frac{4\sqrt{6}}{5}=\frac{H}{\frac{1}{2}a} \quad\bigg/\cdot\frac{1}{2}a \\
H=\frac{4\sqrt{6}}{5}\cdot\frac{1}{2}a \\
H=\frac{2\sqrt{6}}{5}a$$
Krok 3. Wyznaczenie długości krawędzi podstawy (\(a\)).
Z Twierdzenia Pitagorasa wiemy, że:
$$\left(\frac{1}{2}a\right)^2+H^2=22^2 \\
\left(\frac{1}{2}a\right)^2+\left(\frac{2\sqrt{6}}{5}a\right)^2=22^2 \\
\frac{1}{4}a^2+\frac{4\cdot6}{25}a^2=484 \\
\frac{1}{4}a^2+\frac{24}{25}a^2=484 \\
\frac{25}{100}a^2+\frac{96}{100}a^2=484 \quad\bigg/\cdot100 \\
25a^2+96a^2=48400 \\
121a^2=48400 \\
a^2=400 \\
a=20$$
Krok 4. Obliczenie pola podstawy ostrosłupa.
Skoro sama podstawa jest kwadratem to jej pole będzie równe:
$$P_{p}=a^2 \\
P_{p}=20^2 \\
P_{p}=400$$
Krok 5. Obliczenie długości wysokości ostrosłupa.
Podstawiając \(a=20\) do wzoru na wysokość ostrosłupa wyznaczonego w kroku drugim otrzymamy:
$$H=\frac{2\sqrt{6}}{5}\cdot20 \\
H=\frac{40\sqrt{6}}{5} \\
H=8\sqrt{6}$$
Krok 6. Obliczenie objętości ostrosłupa.
Znając miary wysokości ostrosłupa oraz jego pole podstawy możemy bez problemów obliczyć jego objętość:
$$V=\frac{1}{3}\cdot P_{p} \cdot H \\
V=\frac{1}{3}\cdot400\cdot8\sqrt{6} \\
V=\frac{3200\sqrt{6}}{3}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy korzystając z własności tangensa zapiszesz, że \(\frac{4\sqrt{6}}{5}=\frac{H}{\frac{1}{2}a}\) (patrz: Krok 2.).
ALBO
• Gdy korzystając z Twierdzenia Pitagorasa zapiszesz równanie np. \(\left(\frac{1}{2}a\right)^2+H^2=22^2\) (patrz: Krok 3.).
2 pkt
• Gdy wyznaczysz długość krawędzi podstawy \(a=20\) (patrz: Krok 3.).
ALBO
• Gdy zapiszesz układ równań składający się przykładowo z równań: \(\left(\frac{1}{2}a\right)^2+H^2=22^2\) oraz \(\frac{4\sqrt{6}}{5}=\frac{H}{\frac{1}{2}a}\).
3 pkt
• Gdy wyznaczysz długość krawędzi podstawy\(a=20\) (patrz: Krok 3.) oraz obliczysz wysokość ostrosłupa \(H=8\sqrt{6}\) (patrz: Krok 5.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 6. (4pkt) Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(16\). Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy \(\frac{3}{5}\). Oblicz pole powierzchni całkowitej tego graniastosłupa.
Odpowiedź
\(P_{c}=144+384\sqrt{2}\)
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
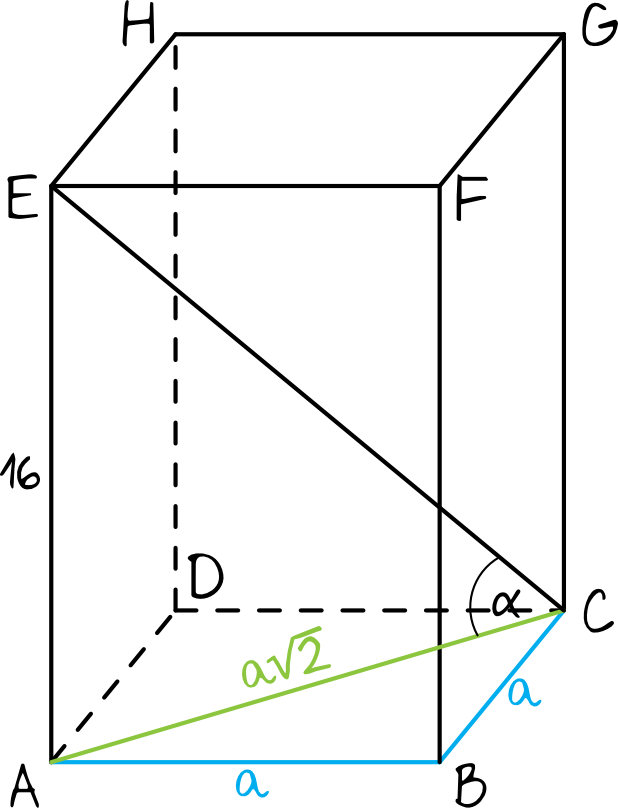
W zadaniu mowa o graniastosłupie prawidłowym czworokątnym, a to oznacza, że w podstawie znajduje się kwadrat. Jeśli więc bok kwadratu oznaczylibyśmy sobie jako \(a\), to przekątna \(|AC|=a\sqrt{2}\).
Kluczem do rozwiązania tego zadania będzie poznanie długości \(a\), bo wtedy obliczymy pole podstawy i pola ścian bocznych.
Krok 2. Obliczenie długości odcinka \(|EC|\).
Spójrzmy na trójkąt \(ACE\). Znamy długość \(|AE|=16\). Wiemy też, że \(|AC|=a\sqrt{2}\). Gdyby więc udało nam się jeszcze ustalić długość odcinka \(|EC|\) to długość \(a\) obliczylibyśmy z Twierdzenia Pitagorasa.
Z pomocą przyjdzie nam informacja mówiąca o tym, że \(cosα=\frac{3}{5}\).
$$cosα=\frac{|AC|}{|EC|} \\
\frac{3}{5}=\frac{a\sqrt{2}}{|EC|} \quad\bigg/\cdot\|EC|\\
\frac{3}{5}|EC|=a\sqrt{2} \quad\bigg/\cdot\frac{5}{3} \\
|EC|=\frac{5\sqrt{2}a}{3}$$
Krok 3. Wyznaczenie długości krawędzi \(a\) z wykorzystaniem Twierdzenia Pitagorasa.
$$a^2+b^2=c^2 \\
|AC|^2+|AE|^2=|EC|^2 \\
(a\sqrt{2})^2+16^2=\left(\frac{5\sqrt{2}a}{3}\right)^2 \\
2a^2+256=\frac{50a^2}{9} \cdot|\cdot9 \\
18a^2+2304=50a^2 \\
-32a^2+2304=0 \quad\bigg/:(-32) \\
a^2-72=0$$
Powstałe równanie możemy obliczyć metodą delty (pamiętaj, że w tym przypadku współczynnik \(b=0\)), ale wygodniej będzie zapisać to w ten sposób:
$$a^2-72=0 \\
a^2=72 \\
a=\sqrt{72} \quad\lor\quad a=-\sqrt{72}$$
Ujemne rozwiązanie oczywiście odrzucamy. To co jeszcze warto zrobić, to wyłączyć wspólny czynnik przed znak pierwiastka, tak więc:
$$a=\sqrt{72}=a=\sqrt{36\cdot2}=6\sqrt{2}$$
Krok 4. Obliczenie pola całkowitego graniastosłupa.
Znając długość \(a=6\sqrt{2}\) możemy już bez przeszkód obliczyć pole całkowite graniastosłupa.
$$P_{c}=2P_{p}+4P_{b} \\
P_{c}=2\cdot a^2+4\cdot a\cdot H \\
P_{c}=2\cdot(6\sqrt{2})^2+4\cdot6\sqrt{2}\cdot16 \\
P_{c}=2\cdot72+384\sqrt{2} \\
P_{c}=144+384\sqrt{2}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy powiążesz ze sobą długości przekątnej podstawy, przekątnej graniastosłupa i wysokości graniastosłupa korzystając z Twierdzenia Pitagorasa (patrz: Krok 2.).
ALBO
• Gdy zapiszesz że \(tgα=\frac{4}{3}\).
ALBO
• Gdy obliczysz długość przekątnej graniastosłupa: \(|EC|=20\)
ALBO
• Gdy zaznaczysz na rysunku kąt nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy.
ALBO
• Gdy obliczysz całe zadanie, ale otrzymany wynik jest niepoprawny bo pomylisz sinusa z cosinusem.
2 pkt
• Gdy zgodnie z przyjętym przez siebie sposobem rozwiązywaniem zadania otrzymasz równanie lub układ równań w którym jedyną niewiadomą jest długość krawędzi podstawy (patrz: Krok 2.). Dopuszczalna jest dowolna forma zapisu np. \(a^2-72=0\) albo \(\frac{16}{a\sqrt{2}}=\frac{4}{3}\) albo \(16^2+(a\sqrt{2})^2=20^2\) itd.
ALBO
• Gdy obliczysz długość przekątnej podstawy graniastosłupa: \(|AC|=12\).
3 pkt
• Gdy obliczysz długość krawędzi podstawy (patrz: Krok 3.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
bardzo przydatne zadania!
Dlaczego w drugim zadaniu liczymy objętość ze wzoru na ostrosłup?
Robimy tak, bo w treści zadania jest podane, że mamy obliczyć objętość ostrosłupa ABCDE, a nie graniastosłupa ;)
Witam, czy w drugim zadaniu nie popełniono błędy przy wyznaczaniu tg 60 stopni. Tg 60 stopni nie powinien być równy AC/AE?
Tangens to stosunek przyprostokątnej leżącej naprzeciwko kąta (czyli u nas AE) względem przyprostokątnej leżącej przy kącie (czyli u nas AC). Jest więc dobrze ;)
Dzień dobry, skąd wiadomo, że w pierwszym zadaniu trójkąt SOC jest prostokątny?
Tak będzie zawsze – wysokość ostrosłupa musi padać prostopadle do płaszczyzny podstawy :)
w zadaniu 3 nie powinno być tg=H/r? przyprostokątna na przeciwko kąta do przyprostokątnej obok kąta
No ale przyprostokątną naprzeciwko kąta jest właśnie r, a przyprostokątną przy kącie jest H, więc będzie to tgα=r/H :)
skąd mam wiedziec np w 2 zadaniu ze trzeba skorzystac z tangensa a nie innych funkcji trygonometrycznych? mam problem z tym ze nie wiem kiedy z czego mam skorzystac
Każda z funkcji trygonometrycznych opisuje relacje między inną parą boków. Jeśli w zadaniu chcemy wykorzystać dwie przyprostokątne (bo np. jedną znamy, a drugiej szukamy), no to w grę wchodzi właśnie tangens, bo tangens opisuje stosunek między długościami przyprostokątnych. Ale gdybyśmy mieli np. przyprostokątną naprzeciwko kąta, a szukalibyśmy przeciwprostokątnej, no to trzeba byłoby skorzystać z sinusa ;)