W geometrii bardzo często wykorzystujemy własności dwóch kluczowych trójkątów prostokątnych, których miary kątów to \(45°, 45°, 90°\) lub \(30°, 60°, 90°\). Przyjrzyjmy się własnościom tych trójkątów i sprawdźmy co dzięki nim jesteśmy w stanie obliczyć.
Własności trójkątów \(45°, 45°, 90°\)
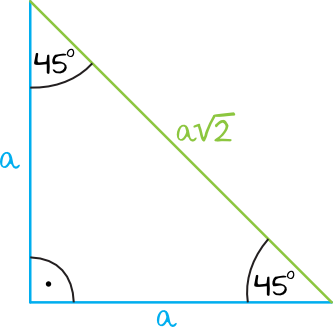
Okazuje się, że istnieje charakterystyczna relacja pomiędzy długościami boków w takim trójkącie. Jeżeli długości przyprostokątnych oznaczymy jako \(a\) to przeciwprostokątna będzie miała zawsze długość \(a\sqrt{2}\). Przy okazji warto zauważyć, że taki trójkąt jest nie tylko prostokątny, ale jest też równoramienny.
Co nam daje taka informacja? Dzięki niej jesteśmy w stanie określić długości wszystkich boków takiego trójkąta, znając tak naprawdę tylko jedną miarę. Załóżmy, że znamy długość \(AB\) powyższego trójkąta, która jest równa \(a=3cm\) i chcemy obliczyć miary pozostałych boków tego trójkąta. Znając własności takich trójkątów możemy stwierdzić, że skoro odcinek \(AB\) ma miarę \(3cm\), to także bok \(BC\) ma długość \(a=3cm\). Przeciwprostokątna \(AC\) będzie za to miała długość \(a\sqrt{2}\), czyli \(3\sqrt{2}cm\). Przećwiczmy te własności na następujących przykładach:

Trójkąt o kątach \(45°, 45°, 90°\) jest trójkątem równoramiennym, więc tak naprawdę obydwie przyprostokątne mają tą samą miarę \(a=4cm\).
Musimy teraz policzyć tylko długość przeciwprostokątnej, a będzie ona równa \(a\sqrt{2}\). Skoro \(a=4cm\), to nasza przeciwprostokątna ma długość \(4\sqrt{2}\).
Znamy już więc wszystkie wymiary trójkąta, zatem na sam koniec musimy obliczyć jeszcze jego obwód:
$$4cm+4cm+4\sqrt{2}cm=8cm+4\sqrt{2}cm$$

Zastanówmy się czego potrzebujemy do obliczenia pola powierzchni. Skoro jest to trójkąt prostokątny, to dolna przyprostokątna jest podstawą trójkąta, a boczna przyprostokątna jest jego wysokością. Potrzebujemy zatem poznać długości tych dwóch przyprostokątnych. Poznamy je wykorzystując ponownie własności trójkąta \(45°, 45°, 90°\). Skoro długość przeciwprostokątnej opisujemy wyrażeniem \(a\sqrt{2}\) i ta długość jest równa \(6\sqrt{2}\), to otrzymamy:
$$a\sqrt{2}=6\sqrt{2} \quad\bigg/: \sqrt{2} \\
a=6$$
W ten sposób udało nam się obliczyć długość jednej i drugiej przyprostokątnej, zatem pole tego trójkąta będzie równe:
$$P=\frac{1}{2}ah \\
P=\frac{1}{2}\cdot6\cdot6 \\
P=3\cdot6 \\
P=18[cm^2]$$
Własności trójkątów \(30°, 60°, 90°\)
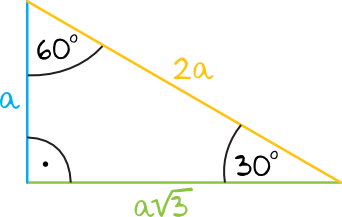
Drugim charakterystycznym trójkątem jest właśnie trójkąt mający kąty o mierze \(30°, 60°, 90°\). Tutaj także znając długość jednego z boków jesteśmy w stanie obliczyć każdą potrzebną miarę, a co za tym idzie – będziemy w stanie wyliczać obwód czy też pole takiego trójkąta. Okazuje się bowiem, że jeżeli długość krótszej przyprostokątnej oznaczymy jako \(a\), to druga przyprostokątna będzie mieć miarę \(a\sqrt{3}\), natomiast przeciwprostokątna będzie mieć miarę \(2a\). Jeżeli więc przykładowo bok \(AB\) ma długość \(a=3cm\), to bok \(BC\) ma długość \(a\sqrt{3}\) czyli \(3\sqrt{3}\), natomiast przeciwprostokątna \(AC\) ma długość \(2a\), czyli \(2\cdot3cm=6cm\).
Musimy jednak uważać na to jak dokładnie wyglądają te relacje między poszczególnymi długościami boków, bo bardzo łatwo jest tutaj o pomyłkę – zwłaszcza jeżeli chodzi o przyprostokątne. Spójrzmy na poniższy rysunek:
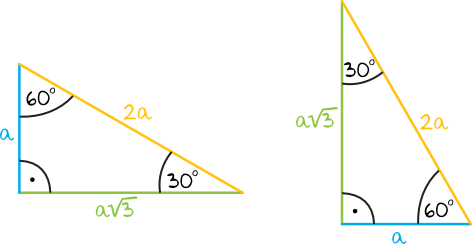
Te dwa trójkąty pokazują, że nie możemy uczyć się zależności w trójkącie \(30°, 60°, 90°\) w taki sposób, że dolna przyprostokątna to jest \(a\), natomiast boczna przyprostokątna to \(a\sqrt{3}\) (a robi tak bardzo wiele osób). Na tym rysunku wyraźnie widać, że taka zasada zapamiętania kompletnie się nie sprawdza kiedy nasz trójkąt zostanie obrócony, a może się tak przecież zdarzyć. Nieco lepszym pomysłem jest pamiętanie, że krótsza przyprostokątna ma długość \(a\), natomiast dłuższa \(a\sqrt{3}\), jednak i ta metoda może czasem nas zawieść, zwłaszcza jak robimy rysunek szkicowy z którego trudno dostrzec która przyprostokątna jest faktycznie krótsza, a która jest dłuższa. Dlatego najlepiej jest zapamiętać, że długość \(a\sqrt{3}\) to długość przyprostokątnej przy kącie \(30°\). Tylko ta metoda jest uniwersalna i na pewno nas nie zawiedzie. Mówi się nawet o tej metodzie „trójka przy trójce”, czyli trójka z pierwiastka ma być przy trójce od \(30°\).
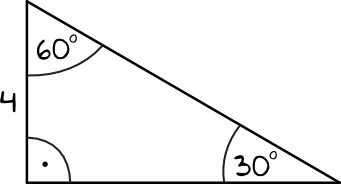
Cała trudność zadania polega na tym, by dobrze określić w którym miejscu jest ta długość \(4cm\). Krótsza przyprostokątna to przyprostokątna leżąca przy kącie \(60°\), stąd też \(a=4cm\). Dłuższa przyprostokątna ma miarę \(a\sqrt{3}\), czyli \(4\sqrt{3}cm\). Przeciwprostokątna ma długość \(2a\), czyli \(2\cdot4cm=8cm\). Obwód tej figury będzie zatem równy:
$$4cm+4\sqrt{3}cm+8cm=12cm+4\sqrt{3}cm$$
Najdłuższym bokiem jest oczywiście przeciwprostokątna (zawsze tak jest, niezależnie od tego jaki to jest trójkąt prostokątny).
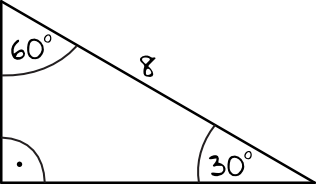
Ta obserwacja pozwala nam stwierdzić, że bok określany długością \(2a\) ma miarę \(8cm\). Najkrótszy bok określamy jako \(a\), czyli jego miara jest równa połowie długości przeciwprostokątnej, zatem \(a=8cm:2=4cm\).

Dziękuję! W końcu to zrozumiałem!
bardzo dziękuje, uratowaliście mnie przed jedynka z kartkówki.
Dzięki, jest prawie 2 w nocy a jutro sprawdzian xd
W takim razie trzymam kciuki! :D
Wysokość w trójkącie 30, 60, 90 to (a√3)/2.
Nie nie, wysokość h=(a√3)/2 jest w trójkącie równobocznym :)
Możesz albo a, 2a, a√3, albo a, a/2, a√3/2. Zauważ, że to jest to samo.
Ok, tak też można, aczkolwiek zwyczajowo przyjmuje się jednak te długości jako właśnie a, 2a, a√3 :)
Ja raz zapomniałem, ale ta najlepsza strona mi pomogła :D
A jak obliczyć obwód takiego trójkąta kiedy a pierwiastek z 3 wynosi 8 pierwiastek z 3 bo mam problem z tym zadaniem
Jeżeli a√3=8√3, to dzielimy obie strony równania przez √3 i wychodzi nam, że a=8 :)
A gdy przeciwprostokątna w trójkącie równoramiennym prostokątnym ma 8 cm, to a jest równe?
To trzeba to zrobić tak jak w tym drugim przykładzie ;)
a√2=8, czyli a=8/√2. Z takiego wyniku można jeszcze usunąć niewymierność z mianownika i wtedy otrzymamy postać a=4√2.
Bardzo dziękuję za pomoc, coś myślę, że w poniedziałek pani zrobi wejściówkę więc lepiej to umieć ;)
Mogło by być więcej zadań, bo naprawdę fajnie się na tym ćwiczy do sprawdzianów i kartkówek. Fajnie tłumaczysz. Prosimy o więcej zadań/przykładów! :)
To najlepsza strona z majcy jaką w życiu widziałem
Dzięki w końcu to zrozumiałem. jest 21:26 i wreszcie to rozumiem.
Czy posiada Pan jakąś książkę z zadaniami lub poleca Pan jakiś zbiór? Przygotowuje się do matury w tym roku i bardzo przydałoby mi się więcej takich zadań jak jest tutaj na stronie :D
Najbardziej to polecić mogę swoje repetytorium, które tworzyłem z uczniami i nauczycielami z całej Polski :D Książka nazywa się „Matbryk” i znajdziesz ją tutaj: https://szaloneliczby.pl/matbryk-matura-podstawowa/
dziękuje !!!! bardzo pomogliście mi w zrozumieniu tego, lecz ciągle sądzę że matma jest trudna
Jejku dziękuję panu. Ratuje mi pan życie, nie było mnie na lekcjach z połowy działu (chora byłam), a notatki koleżanek odbiegały od moich z wyjaśnieniami. Trafiłam na pana stronę z polecenia pani od matematyki, i to był strzał w dziesiątkę. W końcu zrozumiałam te wszystkie pokręcone figury. Sprawdzian mam za dwa dni, także jeszcze mam czas aby się poduczyć. Wpadnę później i powiem co dostałam (oby pozytywne)
Jeszcze Raz dziękuję ❤️❤️❤️
Dzięki za miłe słowa, no i oczywiście trzymam kciuki za jak najlepsze wyniki! :)