Trójkąt \(ABC\) przedstawiony na poniższym rysunku jest równoboczny, a punkty \(B, C, N\) są współliniowe. Na boku \(AC\) wybrano punkt \(M\) tak, że \(|AM|=|CN|\). Wykaż, że \(|BM|=|MN|\).

To zadanie możemy udowodnić tak naprawdę na kilka sposobów, ale najprostszy z nich opierać się będzie na zaznaczeniu punktu \(D\) na odcinku \(BC\) w taki sposób, by odcinek \(MD\) był równoległy do odcinka \(AB\).
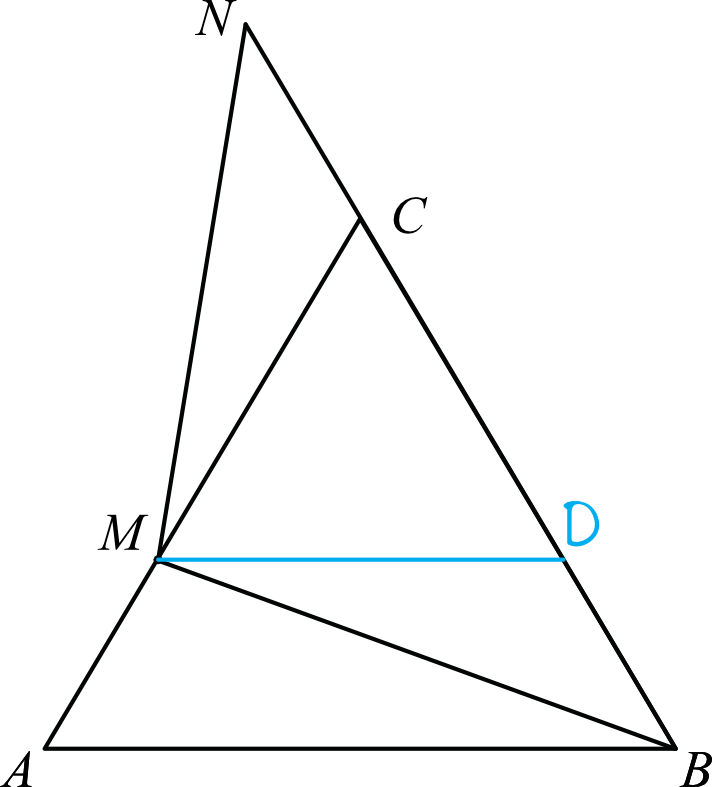
W ten sposób po dorysowaniu prostej równoległej otrzymaliśmy trójkąt równoboczny \(MDC\), co z kolei oznacza, że \(|CM|=|MD|\).
Ale to nie koniec spostrzeżeń. Z treści zadania wiemy, że \(|AM|=|CN|\), a to oznacza, że także \(|BD|=|CN|\).
Jak już sobie powiedzieliśmy wcześniej, dorysowując prostą równoległą w trójkącie równobocznym \(ABC\) otrzymaliśmy mniejszy trójkąt równoboczny \(MDC\). To oznacza, że kąty wewnątrz tej figury są na pewno równe \(60°\). Skoro tak, to korzystając z własności kątów przyległych bez przeszkód wyznaczymy miary kątów \(MCN\) oraz \(BDM\) (patrz: rysunek).
$$|\sphericalangle MCN|=180°-60°=120° \\
|\sphericalangle BDM|=180°-60°=120°$$
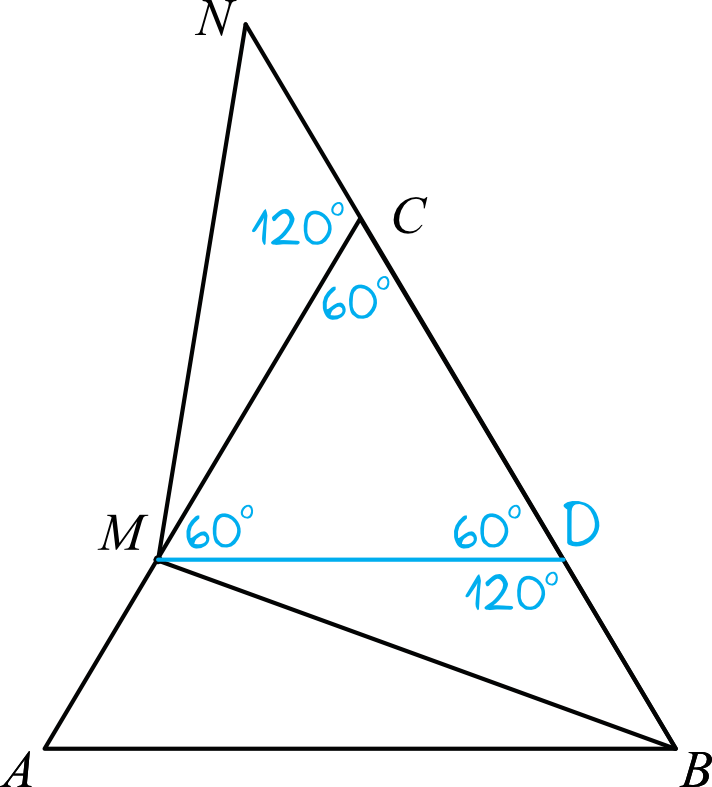
W pierwszym kroku udowodniliśmy że dwie pary boków są tej samej długości: \(|CM|=|MD|\) oraz \(|BD|=|CN|\). W drugim kroku udowodniliśmy, że kąt między tymi bokami ma identyczną miarę. Z powyższych rozważań możemy wywnioskować, że trójkąty \(MCN\) oraz \(MBD\) są przystające zgodnie z zasadą bok-kąt-bok. To kończy nasz dowód, bo skoro trójkąty \(MCN\) oraz \(MBD\) są przystające to \(|BM|=|MN|\).
Udowodniono korzystając z własności kątów przyległych.

