Matura próbna z matematyki (poziom podstawowy) - Operon 2018
Arkusz maturalny zawiera 24 zadania zamknięte oraz 10 zadań otwartych. Łącznie do zdobycia jest 50 punktów, a sugerowany maksymalny czas rozwiązywania to 170 minut.
Zadanie 1. (1pkt) Wynikiem działania \(49^{-6}:7^{-15}\) jest:
Zadanie 2. (1pkt) Wyrażenie \(log_{3}(log30-log3)\) jest równe:
Zadanie 3. (1pkt) Liczbą odwrotną do liczby \(\frac{\sqrt{6}-3}{3}\) jest:
Zadanie 4. (1pkt) Urząd skarbowy został zobowiązany do zwrotu podatku w wysokości \(235,40zł\). Kwotę tę zaokrąglono do pełnych dziesiątek złotych. Błąd względny tego zaokrąglenia wyrażony w procentach wyniósł około:
Zadanie 5. (1pkt) Liczba \(2-2(\sqrt{3}-1)^2\):
Zadanie 6. (1pkt) Nierówność \(\frac{1}{3}-\frac{1}{2}x\lt \frac{1}{6}\) jest równoważna nierówności:
Zadanie 7. (1pkt) Liczba różnych rozwiązań równania \(\frac{3x(x^2-9)}{x-3}=0\) wynosi:
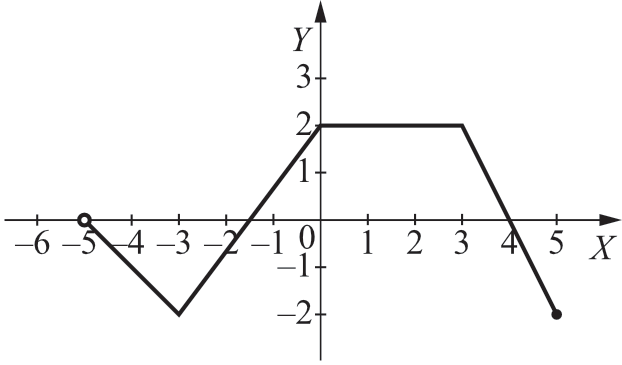
Zadanie 8. (1pkt) Na rysunku przedstawiono wykres pewnej funkcji \(f\). Maksymalny przedział, w którym funkcja \(f\) jest rosnąca, to:
Zadanie 9. (1pkt) Wykres funkcji liniowej \(f(x)=\frac{8-3x}{2}\) przecina osie układu współrzędnych w punktach \(A\) i \(B\). Pole trójkąta \(ABO\), w którym punkt \(O\) jest początkiem układu współrzędnych, wynosi:
Zadanie 10. (1pkt) Zbiorem wartości funkcji \(f(x)=-(x+7)(x-3)\) jest:
Zadanie 11. (1pkt) Wykres funkcji \(f(x)=-3^x\) przesunięto równolegle wzdłuż osi \(OX\) o dwie jednostki w prawo i otrzymano wykres funkcji \(y=g(x)\). Wówczas:
Zadanie 12. (1pkt) Dodatnich wyrazów ciągu określonego wzorem \(a_n=-2n+2018\) dla \(n\ge 1\) jest:
Zadanie 13. (1pkt) Sumę \(n\) początkowych wyrazów ciągu \((4, 6, 9,...)\) można obliczyć ze wzoru:
Zadanie 14. (1pkt) W pewnym ciągu arytmetycznym suma dwóch pierwszych wyrazów jest równa \(5\frac{1}{2}\), a suma trzech pierwszych wyrazów jest równa \(12\). Pierwszy wyraz tego ciągu jest równy:
Zadanie 15. (1pkt) Dla pewnego kąta wypukłego \(α\) mamy \(tg\frac{α}{3}=\frac{\sqrt{3}}{3}\). Kąt \(α\) ma miarę:
Zadanie 16. (1pkt) Wysokość rombu jest równa \(12\), a jego pole jest równe \(180\). Sinus kąta ostrego rombu wynosi:
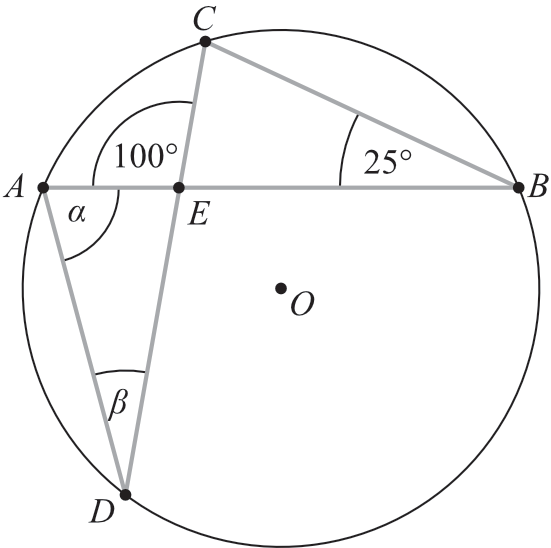
Zadanie 17. (1pkt) Punkty \(A\), \(B\), \(C\) i \(D\) należą do okręgu o środku w punkcie \(O\) (patrz rys.). Suma \(α+β\) wynosi:
Zadanie 18. (1pkt) Obserwowana w laboratorium populacja bakterii podwaja swoją liczebność co \(20\) minut. Początkowa liczba bakterii wynosiła \(K\) sztuk. Oznacza to, że po upływie \(n\) godzin liczebność populacji wyniesie:
Zadanie 19. (1pkt) Przeciwległe wierzchołki kwadratu mają współrzędne \(A=(1,-3)\) i \(C=(-5,3)\). Bok kwadratu ma długość:
Zadanie 20. (1pkt) Ilość wszystkich liczb czterocyfrowych, w których cyfry się nie powtarzają, wynosi:
Zadanie 21. (1pkt) Rzucono trzy razy monetą symetryczną. Prawdopodobieństwo uzyskania jednej reszki wynosi:
Zadanie 22. (1pkt) Średnia arytmetyczna zestawu liczb \(5, 8, 1, 3, x, 8\) wynosi \(6\). Mediana tego zestawu jest równa:
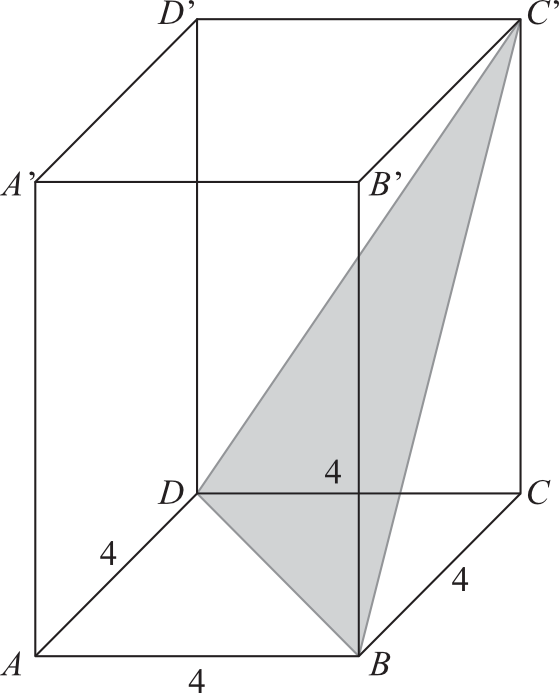
Zadanie 23. (1pkt) Na rysunku przedstawiono graniastosłup prawidłowy czworokątny o krawędzi podstawy równej \(4\). Graniastosłup ten przecięto płaszczyzną przechodzącą przez przekątną \(BD\) podstawy i wierzchołek \(C'\). Otrzymany przekrój jest trójkątem, którego wysokość poprowadzona z wierzchołka \(C'\) jest równa \(12\). Wysokość graniastosłupa jest równa:
Zadanie 24. (1pkt) Kula o promieniu \(6cm\) i walec o wysokości równej \(4,5cm\) mają równe objętości. Średnica podstawy walca ma długość:
Zadanie 25. (2pkt) Rozwiąż nierówność \((2x-5)(3-x)\gt-66\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz miejsca zerowe, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe funkcji (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).
Wyjaśnienie:
Krok 1. Doprowadzenie nierówności do postaci ogólnej.
Zanim zaczniemy liczyć deltę, to musimy przenieść wszystkie wyrazy na lewą stronę, doprowadzając nierówność do postaci ogólnej, zatem:
$$(2x-5)(3-x) \gt -66 \\
6x-2x^2-15+5x \gt -66 \\
6x-2x^2-15+5x+66 \gt 0 \\
-2x^2+11x+51\gt0$$
Krok 2. Wyznaczenie miejsc zerowych.
Teraz zgodnie z zasadami rozwiązywania nierówności szukamy miejsc zerowych, czyli przyrównujemy wartość \(-2x^2+11x+51\) do zera. Mamy więc do rozwiązania równanie kwadratowe w postaci ogólnej \(-2x^2+11x+51=0\), które rozwiążemy klasycznie obliczając deltę:
Współczynniki: \(a=-2,\;b=11,\;c=51\)
$$Δ=b^2-4ac=11^2-4\cdot(-2)\cdot51=121-(-408)=121+408=529 \\
\sqrt{Δ}=\sqrt{529}=23$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-11-23}{2\cdot(-2)}=\frac{-34}{-4}=8\frac{1}{2} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-11+23}{2\cdot(-2)}=\frac{12}{-4}=-3$$
Krok 3. Szkicowanie wykresu paraboli.
Parabola będzie mieć ramiona skierowane do dołu, bo współczynnik kierunkowy \(a\) jest ujemny. Rysujemy oś, zaznaczamy wyznaczone miejsce zerowe i szkicujemy parabolę:
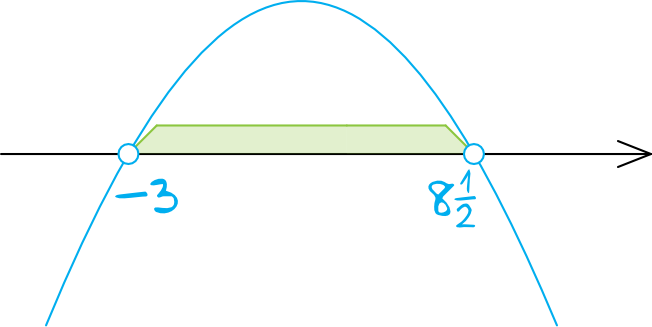
Krok 4. Odczytanie rozwiązania.
Interesują nas wartości większe od zera, zatem patrzymy się na to co jest nad osią. To oznacza, że rozwiązaniem nierówności jest przedział.
$$x\in\left(-3;8\frac{1}{2}\right)$$
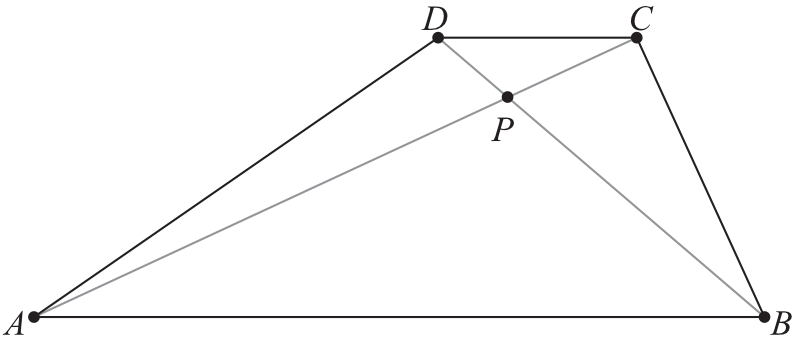
Zadanie 26. (2pkt) W trapezie \(ABCD\) przekątne przecinają się w punkcie \(P\). Punkt \(P\) dzieli przekątne na odcinki długości: \(|AP|=8\), \(|PC|=3\) i \(|BP|=12\). Długości podstaw \(AB\) i \(CD\) trapezu różnią się o \(15\). Oblicz długość odcinka \(DP\) oraz długości podstaw \(AB\) i \(CD\) trapezu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy dostrzeżesz podobieństwo trójkątów (patrz: Krok 1.) i układając proporcję wyznaczysz poprawnie długość jednego z odcinków (patrz: Krok 2. lub Krok 3.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Dostrzeżenie trójkątów podobnych.
W naszym trapezie trójkąty \(ABP\) oraz \(DCP\) są trójkątami podobnymi, bo mają one identyczne miary kątów (cecha kąt-kąt-kąt). Ogólnie warto pamiętać o tej własności trapezów, a wynika ona wprost z własności kątów naprzemianległych i wierzchołkowych:
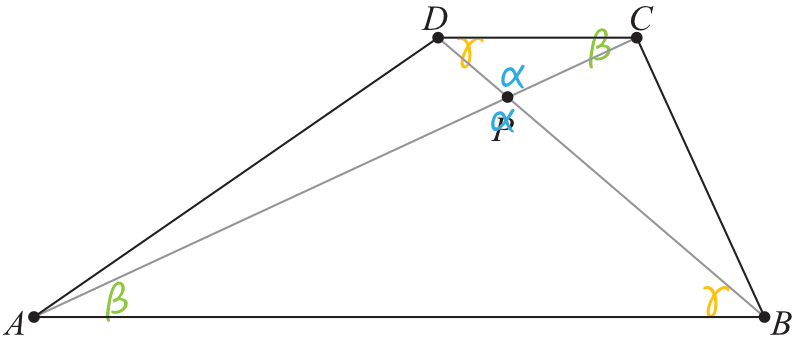
Aby łatwiej było dostrzec poszczególne zależności w trójkątach podobnych, to narysujmy sobie te dwa trójkąty obok siebie, zaznaczając przy okazji wymiary z treści zadania:
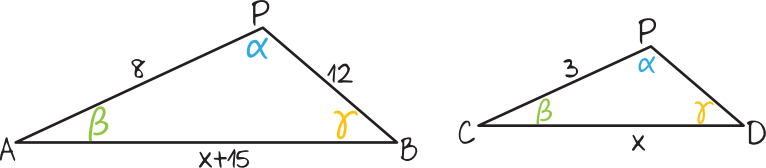
Krok 2. Wyznaczenie długości odcinka \(DP\).
Skoro trójkąty \(ABP\) oraz \(DCP\) są podobne to możemy ułożyć następującą proporcję:
$$\frac{|BP|}{|DP|}=\frac{|AP|}{|CP|} \\
\frac{12}{|DP|}=\frac{|8|}{|3|}$$
Mnożąc teraz na krzyż otrzymamy:
$$12\cdot3=|DP|\cdot8 \\
8|DP|=36 \\
|DP|=4,5$$
Krok 3. Obliczenie długości podstawy \(CD\).
Ponownie korzystając z trójkątów podobnych i z informacji o tym, że podstawy \(AB\) oraz \(CD\) różnią się o \(15\) możemy zapisać, że:
$$\frac{|AB|}{|CD|}=\frac{|AP|}{|CP|} \\
\frac{x+15}{x}=\frac{8}{3}$$
Mnożąc na krzyż otrzymamy:
$$(x+15)\cdot3|=x\cdot8 \\
3x+45=8x \\
45=5x \\
x=9$$
To oznacza, że \(|CD|=9\).
Krok 4. Obliczenie długości podstawy \(AB\).
Podstawa \(AB\) jest o \(15\) dłuższa od podstawy \(CD\), zatem:
$$|AB|=|CD|+15 \\
|AB|=9+15 \\
|AB|=24$$
Uwaga: To zadanie ma zaszyty w sobie pewien ciekawy błąd, bowiem taki trapez nie istnieje. Skąd to wiemy? Jak spojrzymy na trójkąt \(ABP\) to zauważymy, że jego boki mają długość \(24, 12, 8\). Taki trójkąt nie może istnieć, bo jedną z własności trójkątów jest to, że suma dwóch krótszych boków trójkąta musi być większa niż długość najdłuższego boku trójkąta. W naszym przypadku suma dwóch najkrótszych boków jest równa \(8+12=20\), czyli jest mniejsza od \(24\). To jest dowód na to, że trapez o wymiarach boków z treści zadania tak naprawdę nie istnieje.
Zadanie 27. (2pkt) Wykaż, że jeżeli liczby \(a\) i \(b\) są kolejnymi liczbami naturalnymi, to liczba \(\left(a+\frac{1}{2}b\right)^2-\left(a-\frac{1}{2}b\right)^2\) jest podzielna przez \(4\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy doprowadzisz liczbę do postaci \(2ab\) (patrz: Krok 1.), ale nie wyciągniesz z tego wyniku żadnych wniosków.
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Rozpisanie liczby z wykorzystaniem wzorów skróconego mnożenia.
Korzystając z wzorów skróconego mnożenia otrzymamy:
$$\left(a+\frac{1}{2}b\right)^2-\left(a-\frac{1}{2}b\right)^2= \\
=\left(a^2+ab+\frac{1}{4}b^2\right)-\left(a^2-ab+\frac{1}{4}b^2\right)= \\
=a^2+ab+\frac{1}{4}b^2-a^2+ab-\frac{1}{4}b^2=2ab$$
Krok 2. Zakończenie dowodzenia.
Jeżeli liczby \(a\) oraz \(b\) są kolejnymi liczbami naturalnymi, to jedna z nich jest liczbą parzystą. Pomnożenie liczby parzystej przez \(2\) (a pomnożymy ją przez \(2\), bo mamy zapis \(2ab\)) sprawi, że ta liczba na pewno będzie podzielna przez \(4\). W ten sposób dowodzenie można uznać za zakończone.
Zadanie 28. (2pkt) Wiedząc, że kąt \(α\) jest rozwarty oraz \(sin^2α=\frac{9}{25}\), oblicz \(tgα\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz wartość sinusa (patrz: Krok 1.) oraz dostrzeżesz, że \(cos^2α=\frac{16}{25}\).
ALBO
• Gdy obliczysz wartość cosinusa (patrz: Krok 2.).
ALBO
• Gdy błędnie przyjmiesz, że \(cosα=\frac{4}{5}\), a w konsekwencji do tego błędu wyjdzie Ci \(tgα=\frac{3}{4}\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie wartości sinusa.
Wiedząc, że \(sin^2α=\frac{9}{25}\) możemy bez przeszkód obliczyć wartość samego sinusa:
$$sin^2α=\frac{9}{25} \\
sinα=\frac{3}{5} \quad\lor\quad sinα=-\frac{3}{5}$$
Krok 2. Obliczenie wartości cosinusa.
Korzystając z jedynki trygonometrycznej oraz informacji o tym, że \(sin^2α=\frac{9}{25}\) otrzymamy:
$$sin^2α+cos^2α=1 \\
\frac{9}{25}+cos^2α=1 \\
cos^2α=\frac{16}{25} \\
cosα=\frac{4}{5} \quad\lor\quad cosα=-\frac{4}{5}$$
Z treści zadania wynika, że kąt \(α\) jest rozwarty, a dla kątów rozwartych cosinus przyjmuje ujemne wartości. Zatem dodatnie rozwiązanie musimy odrzucić i zostaje nam \(cosα=-\frac{4}{5}\).
Krok 3. Obliczenie wartości tangensa.
Znając wartość sinusa oraz cosinusa możemy już bez przeszkód obliczyć wartość tangensa:
$$tgα=\frac{sinα}{cosα} \\
tgα=\frac{\frac{3}{5}}{-\frac{4}{5}} \\
tgα=\frac{3}{5}:\left(-\frac{4}{5}\right) \\
tgα=\frac{3}{5}\cdot\left(-\frac{5}{4}\right) \\
tgα=-\frac{3}{4}$$
Zadanie 29. (2pkt) Dana jest funkcja \(f(x)=-3x^2+bx+c\) dla \(x\in\mathbb{R}\). Prosta o równaniu \(x=2\) jest osią symetrii paraboli będącej jej wykresem, a zbiorem wartości funkcji \(f\) jest przedział \((-\infty ;21\rangle\). Wyznacz współczynniki \(b\) i \(c\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz funkcję w postaci kanonicznej (patrz: Krok 2.).
ALBO
• Gdy obliczysz wartość współczynnika \(b\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Odczytanie współrzędnych wierzchołka paraboli.
Choć nie jest to zapisane wprost, to z treści zadania możemy wyczytać współrzędne wierzchołka paraboli \(W=(p;q)\). Oś symetrii paraboli wskazuje nam pierwszą współrzędną, czyli współrzędną \(p\), bowiem oś symetrii przechodzi właśnie przez wierzchołek. Skoro osią symetrii jest prosta \(x=2\), to pierwsza współrzędna wierzchołka paraboli będzie równa właśnie \(p=2\).
Drugą współrzędną wskazuje nam zbiór wartości funkcji. Funkcja zawsze ma najmniejszą lub największą wartość w swoim wierzchołku. Skoro maksymalną wartością przyjmowaną przez naszą funkcję jest \(21\), to taka też będzie druga współrzędna wierzchołka paraboli, czyli \(q=21\).
Możemy więc stwierdzić, że \(W=(2;21)\).
Krok 2. Zapisanie wzoru funkcji w postaci kanonicznej.
Znając współrzędne wierzchołka paraboli możemy zapisać wzór funkcji w postaci kanonicznej:
$$f(x)=a(x-p)^2+q$$
Wiemy, że \(a=-3\), bo wynika to z zapisu funkcji w postaci ogólnej \(f(x)=-3x^2+bx+c\). Wiemy też jakie są współrzędne wierzchołka, czyli \(p=2\) oraz \(q=21\), zatem:
$$f(x)=-3(x-2)^2+21$$
Krok 3. Zapisanie wzoru funkcji w postaci ogólnej i odczytanie współczynników \(b\) oraz \(c\).
Teraz znając już wzór funkcji w postaci kanonicznej możemy przekształcić go do postaci ogólnej z której to potem odczytamy potrzebne współczynniki.
$$f(x)=-3(x-2)^2+21 \\
f(x)=-3(x^2-4x+4)+21 \\
f(x)=-3x^2+12x-12+21 \\
f(x)=-3x^2+12x+9$$
To oznacza, że współczynnik \(b=12\) oraz \(c=9\).
Zadanie 30. (2pkt) Do okręgu o środku w punkcie \(O\) poprowadzono z trzech punktów \(A\), \(B\) i \(C\) leżących na okręgu styczne, które przecięły się w punktach \(D\), \(E\) i \(F\) (zobacz rysunek). Wykaż, że jeżeli \(|AF|=x\), to obwód trójkąta \(DEF\) jest równy \(2x\).
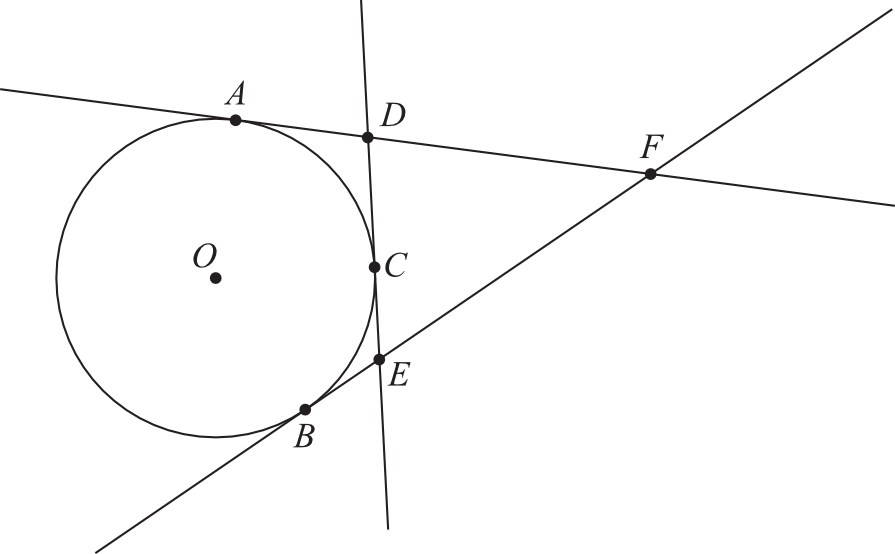
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy dostrzeżesz trzy pary odcinków o równej długości (patrz: Krok 2.).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Dostrzeżenie odcinków o jednakowej długości.
Z własności stycznych do okręgu powinniśmy zauważyć trzy pary boków o identycznych miarach:
$$|DC|=|AD| \\
|CE|=|BE| \\
|AF|=|BF|$$
Krok 2. Rozpisanie długości obwodu trójkąta.
Patrząc się na rysunek możemy zapisać, że obwód trójkąta będzie równy:
$$Obw=|EF|+|DF|+|DC|+|CE|$$
W pierwszym kroku zapisaliśmy sobie, że odcinek \(DC\) ma taką samą miarę jak odcinek \(AD\) oraz że odcinek \(CE\) ma taką samą miarę jak odcinek \(BE\). Podmieniając te dwa odcinki w naszym powyższym zapisie otrzymamy:
$$Obw=\color{green}{|EF|}+\color{blue}{|DF|+|AD|}+\color{green}{|BE|}$$
Teraz spójrzmy na nasze działanie. Z treści zadania wynika, że odcinek \(AF\) ma długość \(x\), a na odcinek \(AF\) składa się suma \(\color{blue}{|AD|+|DF|}\). Podobnie jest z odcinkiem \(BF\) na którego składa się suma \(\color{green}{|BE|+|EF|}\). To by oznaczało, że:
$$Obw=|AF|+|BF| \\
Obw=x+x \\
Obw=2x$$
Otrzymaliśmy oczekiwaną wartość, zatem dowodzenie można uznać za zakończone.
Zadanie 31. (2pkt) Spośród wszystkich wierzchołków sześciokąta foremnego o krawędzi \(1\) losujemy dowolne dwa. Oblicz prawdopodobieństwo tego, że wylosowane wierzchołki utworzą odcinek, którego długość jest liczbą niewymierną.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy wykonasz wszystkie kroki, ale otrzymasz wynik większy od \(1\).
1 pkt
• Gdy obliczysz liczbę wszystkich zdarzeń elementarnych (patrz: Krok 2.)
ALBO
• Gdy obliczysz liczbę wszystkich zdarzeń sprzyjających (patrz: Krok 3.)
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Zastanówmy się jakie odcinki mogą nam wyjść kiedy wylosujemy dwa wierzchołki sześciokąta. Możemy spotkać się z jedną z trzech sytuacji:

• w pierwszej sytuacji kiedy wylosowane punkty są sąsiadującymi wierzchołkami to otrzymamy odcinek o długości \(1\).
• w drugiej sytuacji wylosowane punkty mogą utworzyć dłuższą przekątną sześciokąta. Jej długość jest równa \(1+1=2\), co widać wyraźnie na naszym rysunku (dłuższe przekątne podzieliły nam sześciokąt na sześć trójkątów równobocznych).
• w trzeciej sytuacji wylosowane punkty mogą utworzyć krótszą przekątną sześciokąta. Jej długość jest zgodnie z własnościami trójkątów o kątach \(30°,60°,90°\) równa \(\sqrt{3}\).
Krok 2. Ustalenie liczby wszystkich możliwych zdarzeń elementarnych.
Analizując nasz sześciokąt możemy dostrzec, że losując dwa dowolne wierzchołki możemy otrzymać:
• \(6\) boków o długości \(1\) (to będą boki sześciokąta)
• \(3\) dłuższe przekątne o długości \(2\)
• \(6\) krótszych przekątnych o długości \(\sqrt{3}\) (utworzą one taką gwiazdkę)
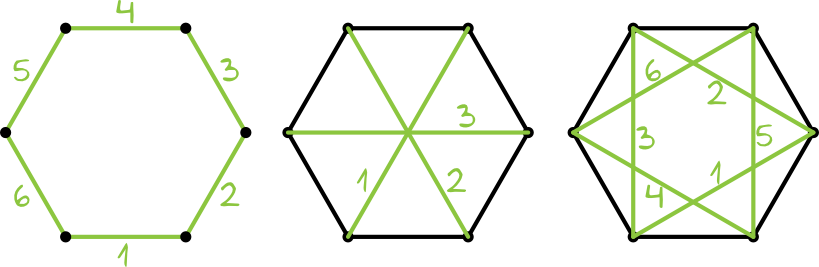
Łącznie jest to \(6+3+6=15\) różnych odcinków. Możemy więc zapisać, że \(|Ω|=15\).
Krok 3. Ustalenie liczby zdarzeń sprzyjających.
Zdarzeniami sprzyjającymi będzie wylosowanie odcinka o długości niewymiernej, czyli w tym przypadku o długości \(\sqrt{3}\). Mamy takich \(6\) odcinków, zatem \(|A|=6\).
Krok 4. Obliczenie prawdopodobieństwa.
Prawdopodobieństwo obliczymy korzystając ze wzoru:
$$P(A)=\frac{|A|}{|Ω|}=\frac{6}{15}=\frac{2}{5}$$
UWAGA: Zadanie jest dość mylące, bowiem tak prawdę mówiąc nigdzie nie jest powiedziane, że nie można byłoby wylosować dwóch tych samych wierzchołków i tym samym długość takiego odcinka byłaby równa \(0\). Powiększyłaby nam się w ten sposób o \(6\) liczba możliwych zdarzeń elementarnych. Moim zdaniem jeżeli ktoś na prawdziwej maturze obliczyłby to zadanie w taki sposób, otrzymując prawdopodobieństwo równe \(\frac{6}{21}=\frac{2}{7}\), to zadanie też byłoby uznane.
Zadanie 32. (3pkt) Dany jest skończony, pięciowyrazowy ciąg \((4a-5;\;a;\;b;\;b+2;\;9)\). Trzy pierwsze wyrazy tego ciągu są trzema kolejnymi wyrazami ciągu arytmetycznego, a trzy ostatnie są trzema kolejnymi wyrazami ciągu geometrycznego. Oblicz \(a\) i \(b\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie zapiszesz równania z których można obliczyć liczbę \(a\) oraz \(b\) (patrz: Krok 1.).
ALBO
• Gdy obliczysz wartość jednej z liczb: \(a\) lub \(b\), ale niepotrzebnie odrzucisz któreś z otrzymanych rozwiązań (patrz: Krok 2. lub Krok 3.).
2 pkt
• Gdy obliczysz obydwie wartości liczby \(b\) (patrz: Krok 2.).
ALBO
• Gdy obliczysz obydwie wartości liczby \(a\) (patrz: Krok 3.).
ALBO
• Gdy obliczysz wartości liczb \(a\) oraz \(b\), ale niepotrzebnie odrzucisz któreś z otrzymanych rozwiązań (patrz: Krok 2. oraz Krok 3.).
ALBO
• Gdy otrzymanych rozwiązań nie połączysz w pary tylko zapiszesz, że rozwiązaniem tego zadania są cztery liczby.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Zapisanie równań wynikających z własności ciągów.
Dla trzech następujących po sobie wyrazów ciągu arytmetycznego zachodzi następująca zależność:
$$a_{2}=\frac{a_{1}+a_{3}}{2}$$
Skoro trzy pierwsze wyrazy, czyli \(4a-5;\;a;\;b\), są trzema kolejnymi wyrazami ciągu arytmetycznego, to korzystając z powyższej własności otrzymamy równanie:
$$a=\frac{4a-5+b}{2}$$
Dla trzech następujących po sobie wyrazów ciągu geometrycznego zachodzi następująca zależność:
$${a_{2}}^2=a_{1}\cdot a_{3}$$
Skoro trzy ostatnie wyrazy, czyli \(b;\;b+2;\;9\), są trzema kolejnymi wyrazami ciągu geometrycznego, to korzystając z powyższej własności otrzymamy równanie:
$$(b+2)^2=b\cdot9 \\
b^2+4b+4=9b \\
b^2-5b+4=0$$
Krok 2. Obliczenie wartości \(b\).
Z zależności wynikającej z własności ciągów geometrycznych otrzymaliśmy równanie kwadratowe \(b^2-5b+4=0\). Rozwiązaniem tego równania będzie nasza niewiadoma \(b\). Skoro tak, to rozwiążmy to równanie, wykorzystując niezawodną deltę:
Współczynniki: \(a=1,\;b=-5,\;c=4\)
$$Δ=b^2-4ac=(-5)^2-4\cdot1\cdot4=25-16=9 \\
\sqrt{Δ}=\sqrt{9}=3$$
$$b_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-5)-3}{2\cdot1}=\frac{5-3}{2}=\frac{2}{2}=1 \\
b_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-5)+3}{2\cdot1}=\frac{5+3}{2}=\frac{8}{2}=4$$
Wyszło nam więc, że są dwie możliwości \(b=1\) oraz \(b=4\) i żadnej z nich nie możemy wykluczyć. Obydwie otrzymane odpowiedzi są jak najbardziej prawidłowe.
Krok 3. Obliczenie wartości \(a\).
W pierwszym kroku korzystając z własności ciągów arytmetycznych otrzymaliśmy równanie \(a=\frac{4a-5+b}{2}\). Skoro znamy już wartość \(b\), to możemy teraz obliczyć wartość \(a\). Z racji tego, że otrzymaliśmy dwa warianty naszej liczby \(b\), to musimy to uwzględnić przy wyznaczaniu wartości \(a\):
Jeżeli \(b=1\), to:
$$a=\frac{4a-5+b}{2} \\
a=\frac{4a-5+1}{2} \\
a=\frac{4a-4}{2} \\
2a=4a-4 \\
-2a=-4 \\
a=2$$
Jeżeli \(b=4\), to:
$$a=\frac{4a-5+b}{2} \\
a=\frac{4a-5+4}{2} \\
a=\frac{4a-1}{2} \\
2a=4a-1 \\
-2a=-1 \\
a=\frac{1}{2}$$
I tu ponownie, żadnego rozwiązania nie możemy wykluczyć. To z kolei oznacza, że to zadanie ma dwa rozwiązania: \(a=2, b=1\) lub też \(a=\frac{1}{2}, b=4\).
Zadanie 33. (4pkt) Dany jest trójkąt \(ABC\), w którym \(A=(-9,8)\). Bok \(BC\) tego trójkąta zawiera się w prostej o równaniu \(y=-2x+38\). Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka \(B\) ma równanie \(3x+2y-61=0\). Wyznacz współrzędne wierzchołków \(B\) i \(C\) oraz napisz równanie prostej zawierającej wysokość trójkąta poprowadzoną z wierzchołka \(C\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz współrzędne wierzchołka \(B\) (patrz: Krok 2.).
2 pkt
• Gdy wyznaczysz równanie prostej \(AC\) (patrz: Krok 4.).
3 pkt
• Gdy wyznaczysz współrzędne wierzchołka \(B\) (patrz: Krok 5.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy sobie szkic całej sytuacji, tak aby mieć lepszy podgląd na to co trzeba zrobić:
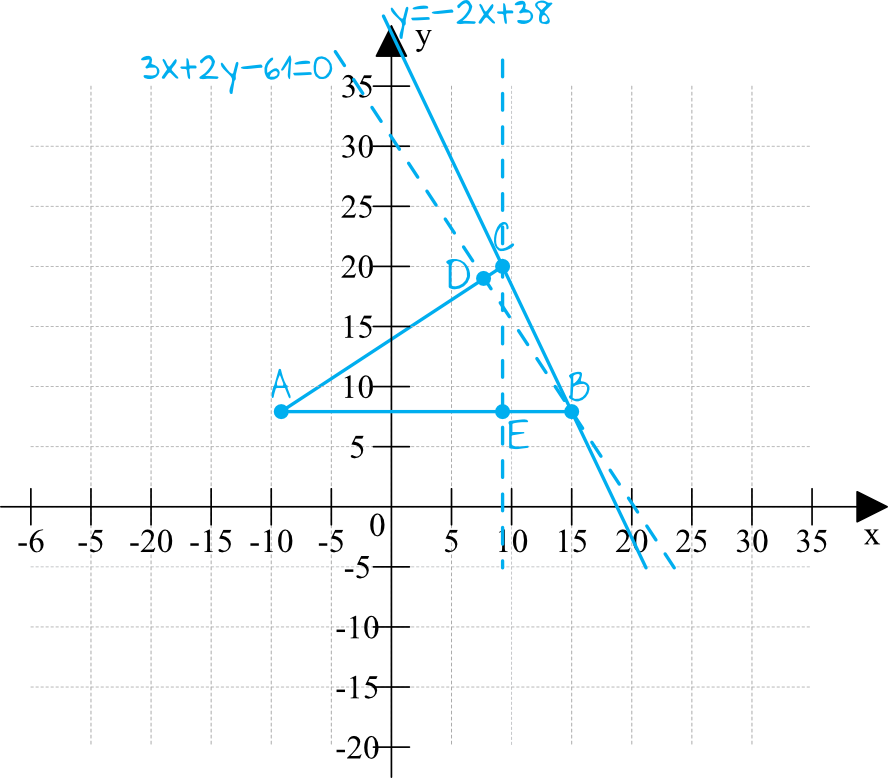
Liniami przerywanymi zostały narysowane wysokości opuszczone z wierzchołka \(B\) oraz \(C\).
Krok 2. Wyznaczenie współrzędnych punktu \(B\).
Z treści zadania (i tym samym z rysunku) wynika, że proste o równaniu \(y=-2x+38\) oraz \(3x+2y-61=0\) przecinają się w punkcie \(B\). Zgodnie z tak zwaną geometryczną interpretacją układu równań wiemy, że rozwiązaniem układu równań zbudowanego z dwóch prostych będzie miejsce ich przecięcia. W ten sposób będziemy mogli wyznaczyć współrzędne punktu \(B\), zatem:
$$\begin{cases}
y=-2x+38 \\
3x+2y-61=0
\end{cases}$$
Podstawiając pierwsze równanie do drugiego otrzymamy:
$$3x+2\cdot(-2x+38)-61=0 \\
3x-4x+76-61=0 \\
-x+15=0 \\
x=15$$
Znając wartość iksa możemy teraz obliczyć wartość igreka, podstawiając do dowolnego z równań (np. pierwszego) wartość \(x=15\):
$$y=-2x+38 \\
y=-2\cdot15+38 \\
y=-30+38 \\
y=8$$
To oznacza, że \(B=(15,8)\).
Krok 3. Zapisanie równania prostej \(BD\) w postaci kierunkowej.
Prosta \(BD\) będąca wysokością poprowadzoną z wierzchołka \(B\) jest zapisana w postaci ogólnej, a my za chwilę będziemy potrzebować postaci kierunkowej (do wyznaczenia prostej prostopadłej). W związku z tym już teraz przekształćmy ten zapis do wspomnianej postaci kierunkowej:
$$3x+2y-61=0 \\
2y=-3x+61 \\
y=-\frac{3}{2}x+30\frac{1}{2}$$
Krok 4. Wyznaczenie równania prostej \(AC\).
Wiemy, że prosta \(AC\) jest prostopadła do prostej \(BD\). Z własności prostych prostopadłych wynika, że aby dwie proste były względem prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Prosta \(BD\) ma współczynnik kierunkowy równy \(a=-\frac{3}{2}\), zatem prosta \(AC\), czyli prosta prostopadła, będzie mieć ten współczynnik równy \(a=\frac{2}{3}\), bo \(-\frac{3}{2}\cdot\frac{2}{3}=-1\). To oznacza, że prosta \(AC\) wyraża się równaniem \(y=\frac{2}{3}x+b\). Brakuje nam jeszcze wartości współczynnika \(b\), a poznamy go podstawiając do tego równania współrzędne punktu \(A\), czyli \(x=-9\) oraz \(y=8\):
$$y=\frac{2}{3}x+b \\
8=\frac{2}{3}\cdot(-9)+b \\
8=-6+b \\
b=14$$
Skoro współczynnik \(b=14\) to prosta \(AC\) wyraża się równaniem \(y=\frac{2}{3}x+14\).
Krok 5. Wyznaczenie współrzędnej punktu \(C\).
Zastosujemy identyczny zabieg co przy wyznaczaniu współrzędnych punktu \(B\). Punkt \(C\) jest miejscem przecięcia się prostych \(y=-2x+38\) oraz \(y=\frac{2}{3}x+14\), zatem jego współrzędne obliczymy rozwiązując następujący układ równań:
\begin{cases}
y=-2x+38 \\
y=\frac{2}{3}x+14
\end{cases}
Podstawiając pierwsze równanie do drugiego otrzymamy:
$$-2x+38=\frac{2}{3}x+14 \quad\bigg/\cdot3 \\
-6x+114=2x+42 \\
-8x=-72 \\
x=9$$
Znając wartość iksa możemy teraz obliczyć wartość igreka, podstawiając do dowolnego z równań (np. pierwszego) wartość \(x=9\):
$$y=-2x+38 \\
y=-2\cdot9+38 \\
y=-18+38 \\
y=20$$
To oznacza, że \(C=(9,20)\).
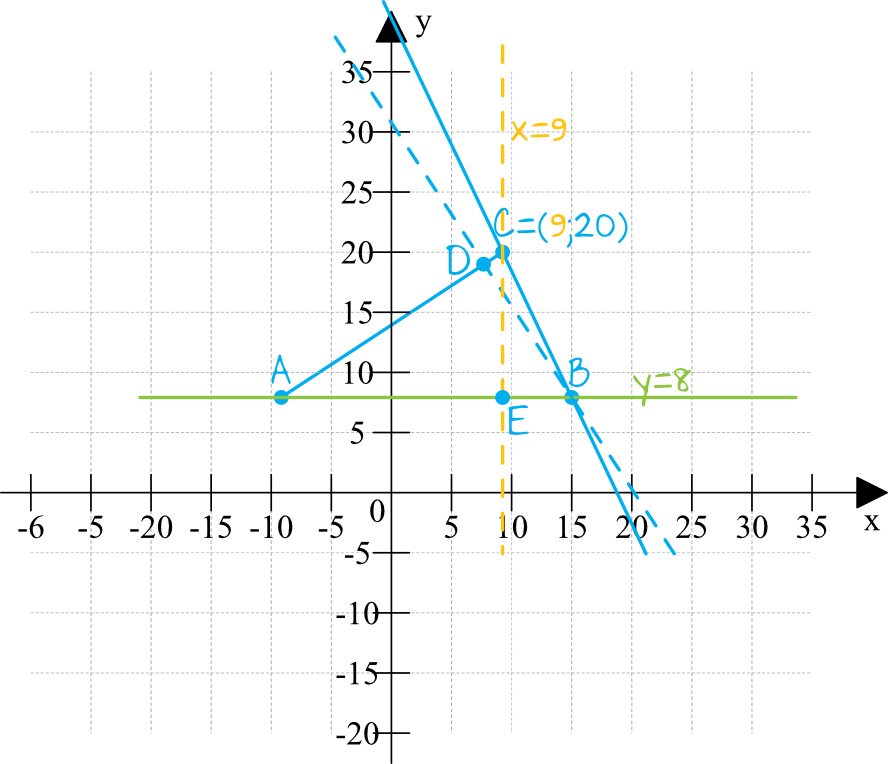
Krok 6. Wyznaczenie równania prostej \(CE\).
Poszukiwana przez nas prosta \(CE\) (czyli wysokość opuszczona z wierzchołka \(C\)) jest prostopadła do prostej \(AB\). Teoretycznie powinniśmy najpierw obliczyć jakie jest równanie prostej \(AB\), a potem obliczyć równanie prostej \(CE\), ale da się poznać wzór tej prostej znacznie szybciej.
Powinniśmy zauważyć, że punkty \(A\) i \(B\) mają jednakową współrzędną igrekową, czyli leżą "na tej samej linii". Bez żadnych więc obliczeń możemy zapisać, że prosta \(AB\) wyraża się równaniem \(y=8\). Prostymi prostopadłymi do tej prostej byłyby więc np. \(x=1\), \(x=3\) czy też \(x=7\). Nas interesuje taka prosta prostopadła, która przejdzie przez punkt \(C=(9,20)\), czyli przejdzie przez współrzędną iksową równą \(9\). Z tego też względu interesująca nas prosta \(CE\) wyrazi się wzorem \(x=9\).
Zadanie 34. (5pkt) W ostrosłupie prawidłowym trójkątnym krawędź boczna jest trzy razy dłuższa od wysokości ostrosłupa. Krawędź podstawy ma długość \(12\). Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość odcinka \(PC\) (patrz: Krok 3.).
2 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 4.).
3 pkt
• Gdy obliczysz wysokość ściany bocznej (patrz: Krok 6.).
ALBO
• Gdy obliczysz objętość ostrosłupa (patrz: Krok 7.).
4 pkt
• Gdy obliczysz wysokość ściany bocznej (patrz: Krok 6.) oraz obliczysz objętość ostrosłupa (patrz: Krok 7.) lub pole powierzchni bocznej (patrz: Krok 8.)
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Aby przystąpić do obliczeń sporządźmy prosty rysunek pomocniczy, zaznaczając na nim dane z treści zadania:
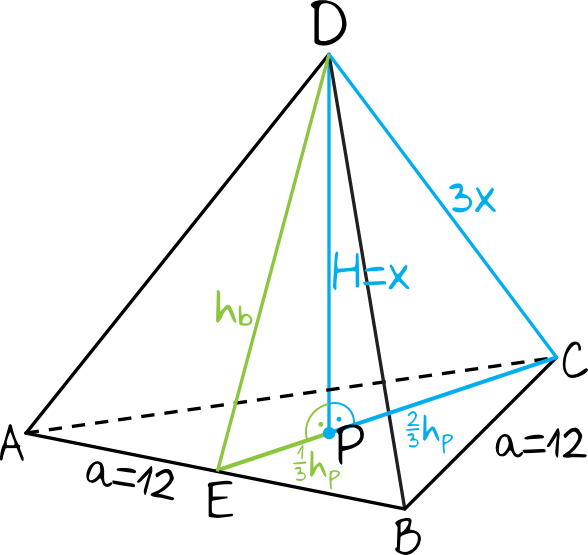
Krok 2. Obliczenie wysokości trójkąta znajdującego się w podstawie.
Ostrosłup jest prawidłowy, zatem w podstawie musi znaleźć się trójkąt równoboczny. Wiemy, że bok tego trójkąta ma długość \(a=12\), zatem wysokość podstawy będzie równa:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
h_{p}=\frac{12\sqrt{3}}{2} \\
h_{p}=6\sqrt{3}$$
Krok 3. Obliczenie długości dolnej przyprostokątnej niebieskiego trójkąta prostokątnego.
Zgodnie z naszym rysunkiem (i zgodnie z własnościami trójkątów równobocznych), dolna przyprostokątna niebieskiego trójkąta prostokątnego stanowi \(\frac{2}{3}\) wysokości trójkąta równobocznego, który znalazł się w podstawie. W związku z tym:
$$PC=\frac{2}{3}h_{p} \\
PC=\frac{2}{3}\cdot6\sqrt{3} \\
PC=4\sqrt{3}$$
Krok 4. Obliczenie wysokości ostrosłupa.
Ponownie spoglądamy na niebieski trójkąt prostokątny. Korzystając z Twierdzenia Pitagorasa możemy teraz zapisać, że:
$$|PC|^2+|PD|^2=|CD|^2 \\
(4\sqrt{3})^2+x^2=(3x)^2 \\
16\cdot3+x^2=9x^2 \\
8x^2=48 \\
x^2=6 \\
x=\sqrt{6} \quad\lor\quad x=-\sqrt{6}$$
Ujemną wartość oczywiście odrzucamy, bo wysokość nie może być ujemna, czyli już wiemy, że wysokość naszego ostrosłupa to \(H=\sqrt{6}\).
Krok 5. Obliczenie długości dolnej przyprostokątnej zielonego trójkąta prostokątnego.
Zgodnie z naszym rysunkiem dolna przyprostokątna zielonego trójkąta prostokątnego ma długość \(\frac{1}{3}\) wysokości trójkąta równobocznego, który znalazł się w podstawie, zatem:
$$EP=\frac{1}{3}h_{p} \\
EP=\frac{1}{3}\cdot6\sqrt{3} \\
EP=2\sqrt{3}$$
Krok 6. Obliczenie wysokości ściany bocznej.
Do obliczenia pola powierzchni bocznej musimy znać wysokość ściany bocznej. W tym celu spoglądamy na nasz zielony trójkąt prostokątny i korzystając z Twierdzenia Pitagorasa otrzymamy:
$$|EP|^2+|PD|^2=|ED|^2 \\
(2\sqrt{3})^2+(\sqrt{6})^2=|ED|^2 \\
4\cdot3+6=|ED|^2 \\
12+6=|ED|^2 \\
|ED|^2=18 \\
|ED|=\sqrt{18} \quad\lor\quad |ED|=-\sqrt{18}$$
Długość odcinka nie może być ujemna, zatem zostaje nam \(|ED|=\sqrt{18}\), co możemy jeszcze rozpisać jako \(|ED|=\sqrt{9\cdot2}=3\sqrt{2}\). To oznacza, że wysokość ściany bocznej jest równa \(h_{b}=3\sqrt{2}\).
Krok 7. Obliczenie objętości ostrosłupa.
Mamy już komplet informacji na temat naszego ostrosłupa. Wiemy, że w podstawie jest trójkąt równoboczny o boku \(a=12\), wiemy też że \(H=\sqrt{6}\), zatem:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot\frac{a^2\sqrt{3}}{4}\cdot H \\
V=\frac{1}{3}\cdot\frac{144\sqrt{3}}{4}\cdot\sqrt{6} \\
V=\frac{1}{3}\cdot\frac{144\sqrt{3}}{4}\cdot\sqrt{6} \\
V=\frac{1}{3}\cdot36\sqrt{3}\cdot\sqrt{6} \\
V=12\sqrt{3}\cdot\sqrt{6} \\
V=12\sqrt{18} \\
V=12\sqrt{9\cdot2} \\
V=12\cdot3\sqrt{2} \\
V=36\sqrt{2}$$
Krok 8. Obliczenie pola powierzchni bocznej.
Na pole powierzchni bocznej składają się \(3\) ściany, każda z nich ma podstawę o długości \(a=12\) oraz wysokość \(h_{b}=3\sqrt{2}\). W związku z tym:
$$P_{b}=3\cdot\frac{1}{2}ah \\
P_{b}=3\cdot\frac{1}{2}\cdot12\cdot3\sqrt{2} \\
P_{b}=18\cdot3\sqrt{2} \\
P_{b}=54\sqrt{2}$$