Matura z matematyki (poziom podstawowy) - Czerwiec 2011
Arkusz maturalny zawiera 22 zadania zamknięte oraz 11 zadań otwartych. Łącznie do zdobycia jest 50 punktów, a sugerowany maksymalny czas rozwiązywania to 170 minut.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Liczbę \(\sqrt{20}\) można przedstawić w postaci:
Zadanie 2. (1pkt) Potęga \(\left(\frac{a}{b}\right)^{-5}\) (gdzie \(a\) i \(b\) są różne od zera) jest równa:
Zadanie 3. (1pkt) Liczba \(log_{\frac{1}{2}}8\) jest równa:
Zadanie 4. (1pkt) Wskaż liczbę, która spełnia równanie \(|4x-5|=x\).
Zadanie 5. (1pkt) Cenę pewnego towaru najpierw obniżono o \(20\%\), a następnie nową cenę podwyższono o \(10\%\). W wyniku obu tych zmian cena towaru zmniejszyła się w stosunku do pierwotnej o:
Zadanie 6. (1pkt) Wielomian \(x^2-100\) jest równy:
Zadanie 7. (1pkt) Równanie \(\frac{x^2+25}{x-5}=0\)
Zadanie 8. (1pkt) Najmniejszą liczbą całkowitą spełniającą nierówność \((3-x)(3+x)\gt(3-x)^2\) jest:
Zadanie 9. (1pkt) Funkcja liniowa \(f(x)=-\frac{1}{2}x+3\)
Zadanie 10. (1pkt) Liczby \(x_{1}\), \(x_{2}\) są rozwiązaniami równania \(2(x-5)(x+7)=0\). Suma \(x_{1}+x_{2}\) jest równa:
Zadanie 11. (1pkt) Na rysunku jest przedstawiony wykres funkcji \(y=f(x)\).

Zbiorem wartości tej funkcji jest:
Zadanie 12. (1pkt) W trójkącie prostokątnym dane są kąty ostre: \(α=41°\) i \(β=49°\) . Wtedy \(\frac{cosα+sinβ}{cosα}\) równa się:
Zadanie 13. (1pkt) Ciąg arytmetyczny \((a_{n})\) jest określony wzorem \(a_{n}=2n-1\) dla \(n\ge1\). Różnica tego ciągu jest równa:
Zadanie 14. (1pkt) W ciągu geometrycznym \((a_{n})\) dane są \(a_{2}=\frac{\sqrt{2}}{2}\) i \(a_{3}=-1\). Wtedy wyraz \(a_{1}\) jest równy:
Zadanie 15. (1pkt) Dane są punkty \(A=(-2,2)\) i \(B=(4,-2)\). Współczynnik kierunkowy prostej \(AB\) jest równy:
Zadanie 16. (1pkt) Dany jest okrąg o równaniu \((x+2)^2+(y-3)^2=5\). Środek tego okręgu ma współrzędne:
Zadanie 17. (1pkt) Obwód prostokąta jest równy \(28\). Stosunek długości jego boków jest równy \(3:4\). Dłuższy bok tego prostokąta jest równy:
Zadanie 18. (1pkt) Dany jest trójkąt prostokątny o przyprostokątnych \(6\) i \(8\). Promień okręgu opisanego na tym trójkącie jest równy:
Zadanie 19. (1pkt) Dane są dwa okręgi o promieniach \(12\) i \(17\). Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa:
Zadanie 20. (1pkt) Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych \(6\) i \(13\) wokół krótszej przyprostokątnej. Promień podstawy tego stożka jest równy:
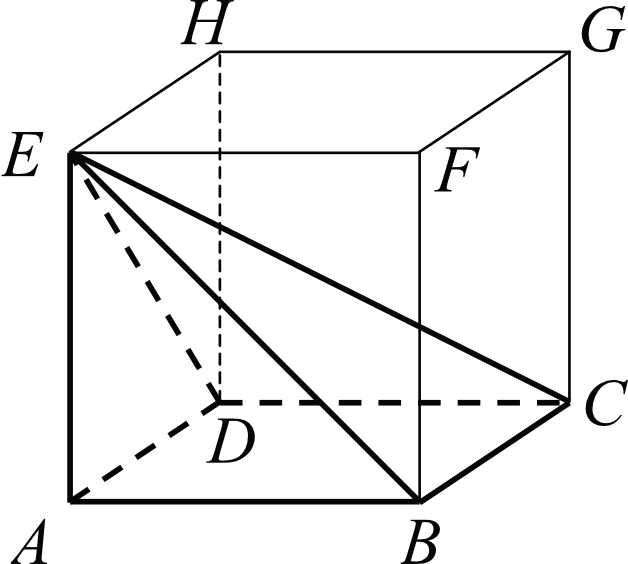
Zadanie 21. (1pkt) Dany jest sześcian \(ABCDEFGH\). Siatką ostrosłupa czworokątnego \(ABCDE\) jest:
Zadanie 22. (1pkt) Jeżeli \(A\) jest zdarzeniem losowym takim, że \(P(A)=6\cdot P(A')\) , oraz \(A'\) jest zdarzeniem przeciwnym do zdarzenia \(A\), to prawdopodobieństwo zdarzenia \(A\) jest równe:
Zadanie 23. (2pkt) Rozwiąż nierówność \(-2x^2+2x+24\ge0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz miejsca zerowe, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe funkcji (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).
Wyjaśnienie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=-2,\;b=2,\;c=24\)
$$Δ=b^2-4ac=2^2-4\cdot(-2)\cdot24=4-(-192)=4+192=196 \\
\sqrt{Δ}=\sqrt{196}=14$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-2-14}{2\cdot(-2)}=\frac{-16}{-4}=4 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-2+14}{2\cdot(-2)}=\frac{12}{-4}=-3$$
Krok 2. Szkicowanie wykresu paraboli.
Ramiona paraboli będą skierowane do dołu, bo współczynnik kierunkowy \(a\) jest ujemny i wynosi \(-2\). Zaznaczamy więc na osi liczbowej miejsca zerowe \(x_{1}=4\) oraz \(x_{2}=-3\) (kropki będą zamalowane, bo w nierówności wystąpił znak \(\ge\)) i szkicujemy wykres paraboli:
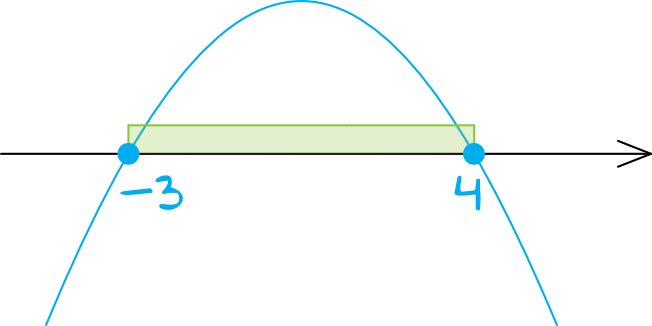
Krok 3. Odczytanie rozwiązania.
Interesują nas wartości większe lub równe zero. Rozwiązaniem tej nierówności będzie więc przedział:
$$x\in\langle-3;4\rangle$$
Zadanie 24. (2pkt) Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x-b}{x-9}\) dla \(x\neq9\), a \(f(14)=5\). Oblicz współczynnik \(b\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy podstawisz dane i otrzymasz równanie \(\frac{2\cdot14-b}{14-9}=5\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Do obliczenia współczynnika \(b\) skorzystamy z informacji, że \(f(14)=5\). Ta informacja mówi nam, że dla argumentu \(x=14\) funkcja przyjmuje wartość równą \(5\). Podstawiając więc te dane do wzoru funkcji otrzymamy:
$$f(x)=\frac{2x-b}{x-9} \\
5=\frac{2\cdot14-b}{14-9} \\
5=\frac{28-b}{5} \quad\bigg/\cdot5 \\
25=28-b \\
b=3$$
Zadanie 25. (2pkt) Trójkąt \(ABC\) przedstawiony na poniższym rysunku jest równoboczny, a punkty \(B, C, N\) są współliniowe. Na boku \(AC\) wybrano punkt \(M\) tak, że \(|AM|=|CN|\). Wykaż, że \(|BM|=|MN|\).

Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy dorysujesz odcinek \(MD\) i dostrzeżesz fakt, że powstaną trójkąty przystające, ale nie udowodnisz tego w żaden geometryczny sposób (np. korzystając z cechy bok-kąt-bok).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Dorysowanie odcinka \(MD\).
To zadanie możemy udowodnić tak naprawdę na kilka sposobów, ale najprostszy z nich opierać się będzie na zaznaczeniu punktu \(D\) na odcinku \(BC\) w taki sposób, by odcinek \(MD\) był równoległy do odcinka \(AB\).
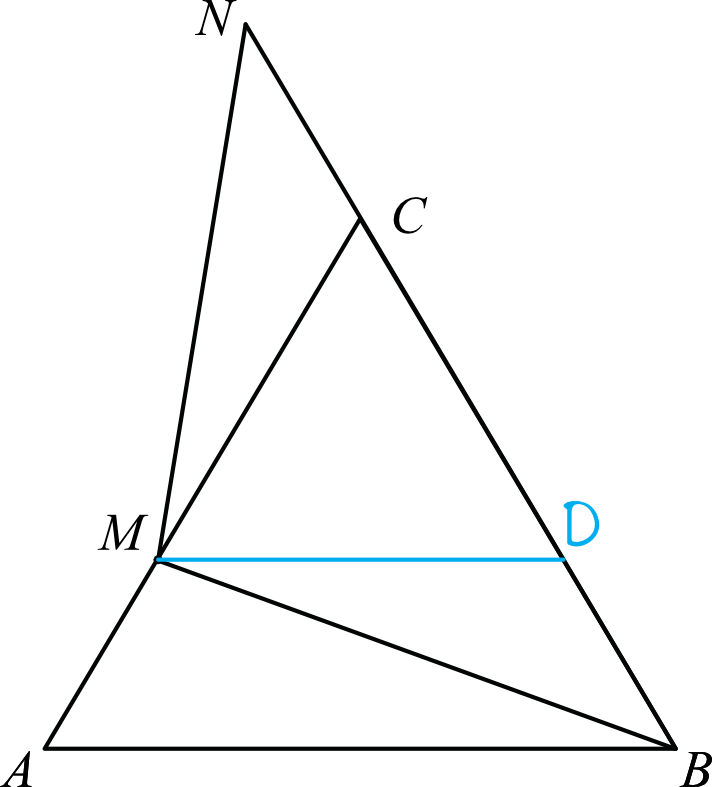
W ten sposób po dorysowaniu prostej równoległej otrzymaliśmy trójkąt równoboczny \(MDC\), co z kolei oznacza, że \(|CM|=|MD|\).
Ale to nie koniec spostrzeżeń. Z treści zadania wiemy, że \(|AM|=|CN|\), a to oznacza, że także \(|BD|=|CN|\).
Krok 2. Obliczenie miar kątów \(MCN\) oraz \(BDM\).
Jak już sobie powiedzieliśmy wcześniej, dorysowując prostą równoległą w trójkącie równobocznym \(ABC\) otrzymaliśmy mniejszy trójkąt równoboczny \(MDC\). To oznacza, że kąty wewnątrz tej figury są na pewno równe \(60°\). Skoro tak, to korzystając z własności kątów przyległych bez przeszkód wyznaczymy miary kątów \(MCN\) oraz \(BDM\) (patrz: rysunek).
$$|\sphericalangle MCN|=180°-60°=120° \\
|\sphericalangle BDM|=180°-60°=120°$$
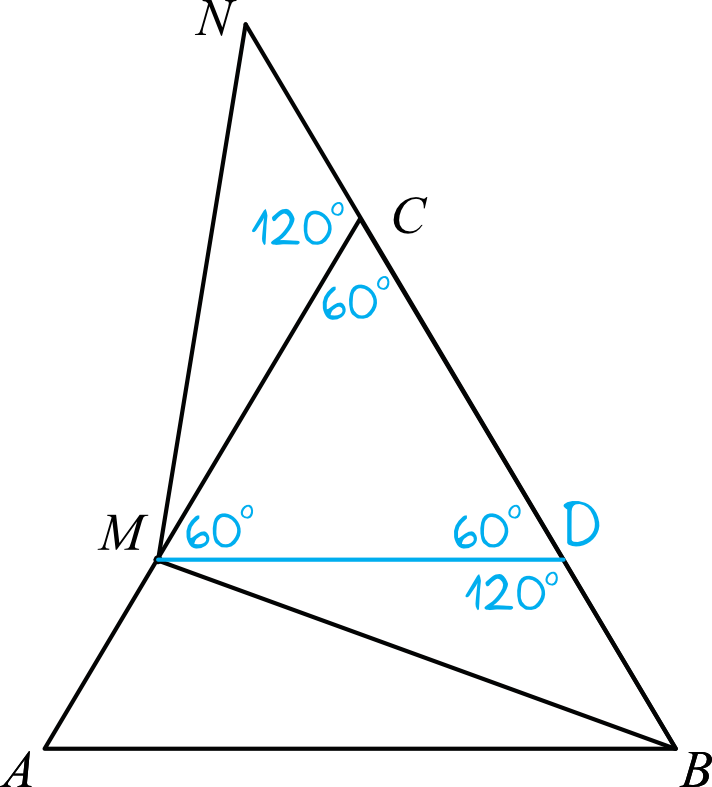
Krok 3. Interpretacja wyników.
W pierwszym kroku udowodniliśmy że dwie pary boków są tej samej długości: \(|CM|=|MD|\) oraz \(|BD|=|CN|\). W drugim kroku udowodniliśmy, że kąt między tymi bokami ma identyczną miarę. Z powyższych rozważań możemy wywnioskować, że trójkąty \(MCN\) oraz \(MBD\) są przystające zgodnie z zasadą bok-kąt-bok. To kończy nasz dowód, bo skoro trójkąty \(MCN\) oraz \(MBD\) są przystające to \(|BM|=|MN|\).
Zadanie 26. (2pkt) Dane są wielomiany \(P(x)=-2x^3+3x^2-1\), \(Q(x)=2x^2-x-1\) oraz \(W(x)=ax+b\). Wyznacz współczynniki \(a\) i \(b\), tak aby wielomian \(P(x)\) był równy iloczynowi \(W(x)\cdot Q(x)\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy uprościsz wielomian do postaci \(2ax^3+(-a+2b)x^2+(-a-b)x-b\) (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wymnożenie wielomianów \(W(x)\) oraz \(Q(x)\).
Skoro iloczyn \(W(x)\cdot Q(x)\) ma być równy \(P(X)\) to poznajmy na początku wartość tego iloczynu:
$$W(x)\cdot Q(x)=(ax+b)\cdot(2x^2-x-1)= \\
=2ax^3-ax^2-ax+2bx^2-bx-b= \\
=2ax^3-ax^2+2bx^2-ax-bx-b= \\
=2ax^3+(-a+2b)x^2+(-a-b)x-b$$
Krok 2. Przyrównanie wielomianu \(P(x)\) do otrzymanego wyniku iloczynu.
Zgodnie z treścią zadania nasz wielomian \(P(x)\) jest równy dokładnie temu, co obliczyliśmy w pierwszym kroku. To pozwoli nam poznać wartości współczynników \(a\) oraz \(b\) bo możemy przyrównać do siebie poszczególne fragmenty tych wielomianów, a konkretniej wartości stojące przed \(x^3\), przed \(x^2\), przed \(x\) oraz wyrazy wolne:
W wielomianie \(P(x)\) przed \(x^3\) mamy liczbę \(-2\). W iloczynie przed \(x^3\) otrzymaliśmy \(2a\). Zatem:
$$-2=2a \\
a=-1$$
W wielomianie \(P(x)\) przed \(x^2\) mamy liczbę \(3\). W iloczynie przed \(x^2\) otrzymaliśmy \(-a+2b\). Wartość \(a\) już znamy, zatem:
$$3=-a+2b \\
3=-(-1)+2b \\
3=1+2b \\
2=2b \\
b=1$$
Dalej już porównywać nie musimy, bo z dwóch pierwszych porównań wyszło nam, że \(a=-1\) oraz \(b=1\).
Zadanie 27. (2pkt) Uzasadnij, że dla każdej dodatniej liczby całkowitej \(n\) liczba \(3^{n+2}-2^{n+2}+3^n-2^n\) jest wielokrotnością liczby \(10\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy podstawisz konkretne wartości liczbowe w miejsce niewiadomej \(n\).
1 pkt
• Gdy doprowadzisz liczbę do postaci \(3^n\cdot10-2^n\cdot5\) i nie udowodnisz dlaczego jest ona wielokrotnością liczby \(10\).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Nasze zadanie tak naprawdę sprowadza się do znalezienia sposobu na wyłączenie przed nawias dziesiątki (lub jej wielokrotności), co ostatecznie udowodniłoby fakt, że ta liczba będzie wielokrotnością \(10\). Całość możemy rozpisać w następujący sposób:
$$3^{n+2}-2^{n+2}+3^n-2^n \\
3^{n+2}+3^n-2^{n+2}-2^n \\
3^n(3^2+1)-2^n(2^2+1) \\
3^n\cdot10-2^n\cdot5 \\
3^n\cdot10-2^{n-1}\cdot2\cdot5 \\
3^n\cdot10-2^{n-1}\cdot10 \\
10\cdot(3^n-2^{n-1})$$
Zadanie 28. (2pkt) Tabela przedstawia wyniki uzyskane na sprawdzianie przez uczniów klasy III.

Oblicz medianę i średnią arytmetyczną uzyskanych ocen.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz tylko medianę (patrz: Krok 2.).
ALBO
• Gdy obliczysz tylko średnią arytmetyczną (patrz: Krok 3.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Uporządkowanie ocen w porządku niemalejącym.
Aby obliczyć medianę musimy na początku uporządkować uzyskane oceny w porządku rosnącym (a precyzyjniej w porządku niemalejącym). Korzystając z tabeli możemy odczytać, że jedynkę otrzymało dwóch uczniów, dwójkę czterech uczniów itd., zatem:
$$1,1,2,2,2,2,3,3,3,3,3,4,4,4,4,4,4,5,5,6$$
Krok 2. Wyznaczenie mediany.
Wszystkich uczniów jest \(1+2+6+5+4+2=20\). Jest to parzysta ilość, zatem medianą będzie średnia arytmetyczna \(10\)-tego oraz \(11\)-tego wyrazu w ciągu który sobie wypisaliśmy w pierwszym kroku. Dziesiątym wyrazem jest liczba \(3\), jedenastym wyrazem jest także liczba \(3\), zatem mediana będzie równa:
$$m=\frac{3+3}{2}=3$$
Krok 3. Obliczenie średniej arytmetycznej.
Aby obliczyć wartość średniej arytmetycznej musimy dodać do siebie wartości wszystkich zdobytych ocen i podzielić je przez liczbę wszystkich uczniów:
$$\bar{a}=\frac{6\cdot1+5\cdot2+4\cdot6+3\cdot5+2\cdot4+1\cdot2}{1+2+6+5+4+2} \\
\bar{a}=\frac{65}{20} \\
\bar{a}=3,25$$
Zadanie 29. (2pkt) Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że liczba oczek w pierwszym rzucie jest o \(1\) mniejsza od liczby oczek w drugim rzucie.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy wykonasz wszystkie kroki, ale otrzymasz wynik większy od \(1\).
1 pkt
• Gdy obliczysz liczbę wszystkich zdarzeń elementarnych (patrz: Krok 1.)
ALBO
• Gdy obliczysz liczbę wszystkich zdarzeń sprzyjających (patrz: Krok 2.)
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Ustalenie liczby wszystkich możliwych zdarzeń elementarnych.
Na każdej kostce może wypaść jeden z sześciu wyników, a skoro rzucamy niezależnie dwoma kostkami, to liczba wszystkich kombinacji będzie równa \(|Ω|=6\cdot6=36\).
Krok 2. Ustalenie liczby zdarzeń sprzyjających.
Sprzyjającymi zdarzeniami (czyli takimi, które spełniają warunki naszego zadania) będą następujące rzuty:
$$(1,2),(2,3),(3,4),(4,5),(5,6)$$
To oznacza, że tylko pięć przypadków spełnia warunki zadania, stąd też możemy napisać, że \(|A|=5\).
Krok 3. Obliczenie prawdopodobieństwa.
Prawdopodobieństwo obliczymy korzystając ze wzoru:
$$P(A)=\frac{|A|}{|Ω|}=\frac{5}{36}$$
Zadanie 30. (2pkt) Liczby \(27, x, 3\) są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz ósmy wyraz tego ciągu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz iloraz ciągu geometrycznego (patrz: Krok 2.)
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wyznaczenie wartości drugiego wyrazu.
Ten krok nie jest konieczny do rozwiązania zadania, ale ułatwia nam odnalezienie ilorazu ciągu geometrycznego. Spróbujmy odnaleźć wartość drugiego wyrazu naszego ciągu geometrycznego. Dla trzech kolejnych liczb ciągu geometrycznego zajdzie równość:
$${a_{2}}^2=a_{1}\cdot a_{3}$$
Podstawiając nasze dane \(a_{1}=27\) oraz \(a_{3}=3\) do tego wzoru otrzymamy:
$${a_{2}}^2=27\cdot3 \\
{a_{2}}^2=81 \\
a_{2}=9 \quad\lor\quad x_{2}=-9$$
Musimy się teraz zastanowić, czy przypadkiem któregoś z otrzymanych wyników nie należy odrzucić.
Gdy \(a_{2}=9\), to mamy ciąg \(27,9,3\), czyli mamy ciąg malejący
Gdy \(a_{2}=-9\), to mamy ciąg \(27,-9,3\), czyli ciąg niemonotoniczny
W treści zadania mamy podaną informację, że nasz ciąg musi być malejący, zatem drugi wyraz tego ciągu musi być równy \(a_{2}=9\).
Krok 2. Wyznaczenie wartości ilorazu ciągu geometrycznego.
Znając przynajmniej dwa następujące po sobie wyrazy ciągu geometrycznego bez przeszkód obliczymy iloraz naszego ciągu.
$$q=\frac{a_{2}}{a_{1}} \\
q=\frac{9}{27} \\
q=\frac{1}{3}$$
Gdybyśmy podeszli do zadania bez wykonywania obliczeń wartości drugiego wyrazu, to iloraz \(q\) moglibyśmy obliczyć korzystając ze wzoru na \(n\)-ty wyraz ciągu geometrycznego:
$$a_{n}=a_{1}\cdot q^{n-1} \\
a_{3}=a_{1}\cdot q^{3-1} \\
a_{3}=a_{1}\cdot q^{2} \\
3=27\cdot q^{2} \\
q^{2}=\frac{1}{9} \\
q=\frac{1}{3} \quad\lor\quad q=-\frac{1}{3}$$
Ciąg ma być malejący, zatem musimy odrzucić \(q=-\frac{1}{3}\) (dla którego ciąg staje się niemonotoniczny). Zostaje nam więc \(q=\frac{1}{3}\).
Krok 3. Obliczenie wartości ósmego wyrazu.
Znamy wartość pierwszego wyrazu, znamy też wartość ilorazu tego ciągu, zatem bez przeszkód obliczymy wartość ósmego wyrazu:
$$a_{n}=a_{1}\cdot q^{n-1} \\
a_{8}=a_{1}\cdot q^{8-1} \\
a_{8}=a_{1}\cdot q^7 \\
a_{8}=27\cdot\left(\frac{1}{3}\right)^7$$
To potęgowanie i mnożenie przez \(27\) możemy obliczyć śmiało na kalkulatorze, ale prawdopodobnie potem będziemy mieć problem ze skróceniem ułamka. Dlatego też jeżeli dobrze opanowaliśmy działania na potęgach to warto to rozpisać nieco sprytniej:
$$a_{8}=3^3\cdot3^{-7} \\
a_{8}=3^{3+(-7)} \\
a_{8}=3^{-4} \\
a_{8}=\frac{1}{81}$$
Zadanie 31. (4pkt) Oblicz sumę wszystkich liczb trzycyfrowych zapisanych wyłącznie za pomocą cyfr \(1, 2, 3, 4\) (cyfry mogą się powtarzać).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz że istnieją \(64\) liczby spełniające warunki zadania.
2 pkt
• Gdy wypiszesz część liczb i zapiszesz jakąś prawidłowość, która związana będzie z kolejnymi liczbami, ale nie obliczysz sumy tych liczb.
ALBO
• Gdy wypiszesz wszystkie liczby spełniające warunki zadania (możesz pominąć maksymalnie trzy z nich), ale nie obliczysz sumy tych liczb.
3 pkt
• Gdy doprowadzisz zadanie do samego końca, ale otrzymany wynik będzie zły jedynie ze względu na błąd rachunkowy lub też ze względu na pominięcie którejś liczby.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
To zadanie jest jednym z tych, które jest dość czasochłonne, bo paradoksalnie najlepszym (a już na pewno najbezpieczniejszym) sposobem byłoby wypisanie tych liczb, a następnie zsumowanie ich wartości. Cyfry mogą się powtarzać, więc skoro na każdym miejscu może się znaleźć jedna z czterech cyfr, to będziemy mieli aż \(4\cdot4\cdot4=64\) kombinacje.
Musielibyśmy więc wypisywać po kolei:
$$111, 112, 113, 114, 121, 122, 123, 124, 131, 132, 133, 134, 141, 142, 143, 144 \\
211, 212, 213, 214...$$
Podczas tego wypisywania możemy jednak dostrzec tutaj pewną prawidłowość, która skróci nasze obliczenia. Tak naprawdę kiedy będziemy wypisywać teraz liczby z cyfrą setek równą \(2\), to każda kolejna liczba będzie o \(100\) większa od analogicznej liczby z cyfrą setek równą \(1\). Przykładowo: \(213-113=100\), albo \(214-114=100\). Możemy więc policzyć sumę tych wszystkich \(16\) liczb z cyfrą setek równą \(1\) i zapisać, że suma liczb z cyfrą setek równą \(2\) będzie o \(16\cdot100=1600\) większa. Analogicznie jak będziemy wypisywać liczby z cyfrą setek równą \(3\), to ich suma będzie o \(16\cdot200=3200\) większa od tych z cyfrą setek równą \(1\) itd. Zatem:
Suma liczb z cyfrą setek równą \(1\) wynosi: \(111+112+113+...+144=2040\)
Suma liczb z cyfrą setek równą \(2\) wynosi: \(2040+16\cdot100=3640\)
Suma liczb z cyfrą setek równą \(3\) wynosi: \(2040+16\cdot200=5240\)
Suma liczb z cyfrą setek równą \(4\) wynosi: \(2040+16\cdot300=6840\)
Suma tych wszystkich liczb jest więc równa:
$$2040+3640+5240+6840=17760$$
Zadanie 32. (4pkt) Podstawą ostrosłupa \(ABCDS\) jest romb \(ABCD\) o boku długości \(4\). Kąt \(ABC\) rombu ma miarę \(120°\) oraz \(|AS|=|CS|=10\) i \(|BS|=|DS|\). Oblicz sinus kąta nachylenia krawędzi \(BS\) do płaszczyzny podstawy ostrosłupa.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długości odcinków \(|CO|=2\sqrt{3}\) oraz \(|BO|=2\) (patrz: Krok 2.).
2 pkt
• Gdy obliczysz wysokość ostrosłupa, czyli \(|SO|=\sqrt{88}=2\sqrt{22}\) (patrz: Krok 3.).
3 pkt
• Gdy obliczysz długość krawędzi bocznej ostrosłupa, czyli \(|BS|=\sqrt{92}=2\sqrt{23}\) (patrz: Krok 4.).
ALBO
• Gdy obliczysz tangens kąta nachylenia krótszej krawędzi bocznej ostrosłupa do płaszczyzny podstawy, czyli \(tgβ=\sqrt{22}\).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Stwórzmy sobie szkic rysunku na którym zaznaczymy wszystkie informacje z treści zadania.
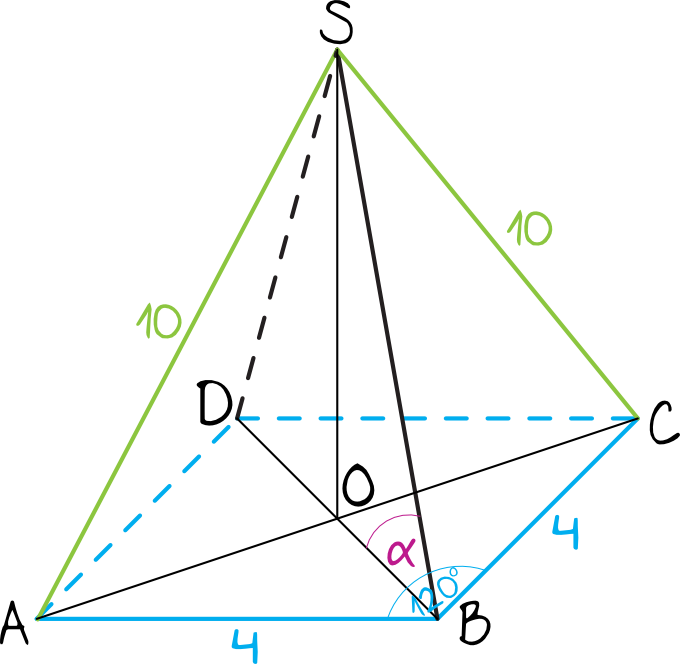
Krok 2. Obliczenie długości odcinków \(CO\) oraz \(BO\).
Wbrew pozorom nie będą to odcinki równej długości, bo przecież przekątne rombu mają różne długości.
Przekątne rombu dzielą kąty przy wierzchołkach na dwie równe części. To oznacza, że kąty \(CBD\) oraz \(CDB\) mają po \(60°\). To z kolei powoduje, że trójkąt \(BCD\) jest trójkątem równobocznym o boku długości \(4\). Analogicznie będzie z trójkątem \(ABD\). Wszystko wyjaśni poniższy rysunek z zaznaczonymi kątami i z niebieskimi liniami, które mówią nam o tym które tworzą dwa trójkąty równoboczne:
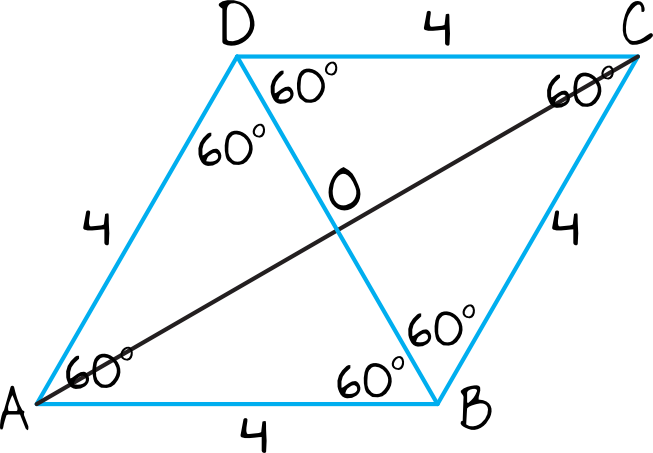
To dla nas bardzo ważna informacja, bo teraz bez przeszkód obliczymy długość odcinka \(CO\), który jest wysokością trójkąta równobocznego \(BCD\) o boku \(a=4\).
$$|CO|=\frac{a\sqrt{3}}{2}=\frac{4\sqrt{3}}{2}=2\sqrt{3}$$
Skoro ustaliliśmy sobie, że trójkąt \(BCD\) jest równoboczny, to znaczy że przekątna \(BD\) ma także długość \(4\). Przekątne w rombie przecinają się w połowie swojej długości, a to pozwoli nam na obliczenie długości boku \(BO\):
$$|BO|=4:2=2$$
Krok 3. Obliczenie długości odcinka \(SO\), czyli wysokości ostrosłupa.
W poprzednim kroku obliczyliśmy długość odcinka \(|CO|=2\sqrt{3}\). Z treści zadania znamy też długość krawędzi \(|SC|=10\). To oznacza, że bez przeszkód obliczymy wysokość \(SO\) naszego ostrosłupa korzystając z Twierdzenia Pitagorasa w trójkącie \(SOC\):
$$a^2+b^2=c^2 \\
|SO|^2+|CO|^2=|SC|^2 \\
|SO|^2+(2\sqrt{3})^2=10^2 \\
|SO|^2+4\cdot3=100 \\
|SO|^2+12=100 \\
|SO|^2=88 \\
|SO|=\sqrt{88} \quad\lor\quad |SO|=-\sqrt{88}$$
Wartość ujemną oczywiście odrzucamy, bo bok musi mieć dodatnią długość i jest ona równa \(|SO|=\sqrt{88}=2\sqrt{22}\).
Krok 4. Obliczenie długości odcinka \(BS\) (czyli naszej krawędzi bocznej).
Tu ponownie skorzystamy sobie z Twierdzenia Pitagorasa, tym razem wobec trójkąta \(BOS\). Znamy wysokości obu przyprostokątnych \(|BO|=2\) (wyliczyliśmy to w drugim kroku) oraz \(|SO|=2\sqrt{22}\) (wyliczyliśmy to w trzecim kroku), więc bez przeszkód wyznaczymy długość krawędzi \(BS\):
$$a^2+b^2=c^2 \\
|BO|^2+|SO|^2=|BS|^2 \\
2^2+(2\sqrt{22})^2=|BS|^2 \\
4+4\cdot22=|BS|^2 \\
|BS|^2=92 \\
|BS|=\sqrt{92} \quad\lor\quad |BS|=-\sqrt{92}$$
Wartość ujemną także oczywiście odrzucamy, więc zostaje nam \(|BS|=\sqrt{92}=2\sqrt{23}\).
Krok 5. Obliczenie wartości sinusa.
Znamy już wszystkie potrzebne miary, więc na koniec musimy obliczyć jeszcze sinus kąta nachylenia krawędzi \(BS\) do płaszczyzny podstawy ostrosłupa:
$$sinα=\frac{|SO|}{|BS|}=\frac{2\sqrt{22}}{2\sqrt{23}}=\frac{\sqrt{22}}{\sqrt{23}}=\sqrt{\frac{22}{23}}$$
Zadanie 33. (4pkt) Wyznacz równanie okręgu przechodzącego przez punkt \(A=(1,8)\) i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz, że współrzędne środka okręgu są równe \(S=(r;r)\) (patrz: Krok 1.).
ALBO
• Gdy zapiszesz, że środek okręgu znajduje się na prostej o równaniu \(y=x\).
2 pkt
• Gdy doprowadzisz do równania kwadratowego w postaci ogólnej z której potem można obliczać deltę (patrz: Krok 2.).
3 pkt
• Gdy doprowadzisz zadanie do samego końca, ale otrzymany wynik będzie zły jedynie ze względu na błąd rachunkowy.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Na początku naszkicujmy sobie opisywaną sytuację:
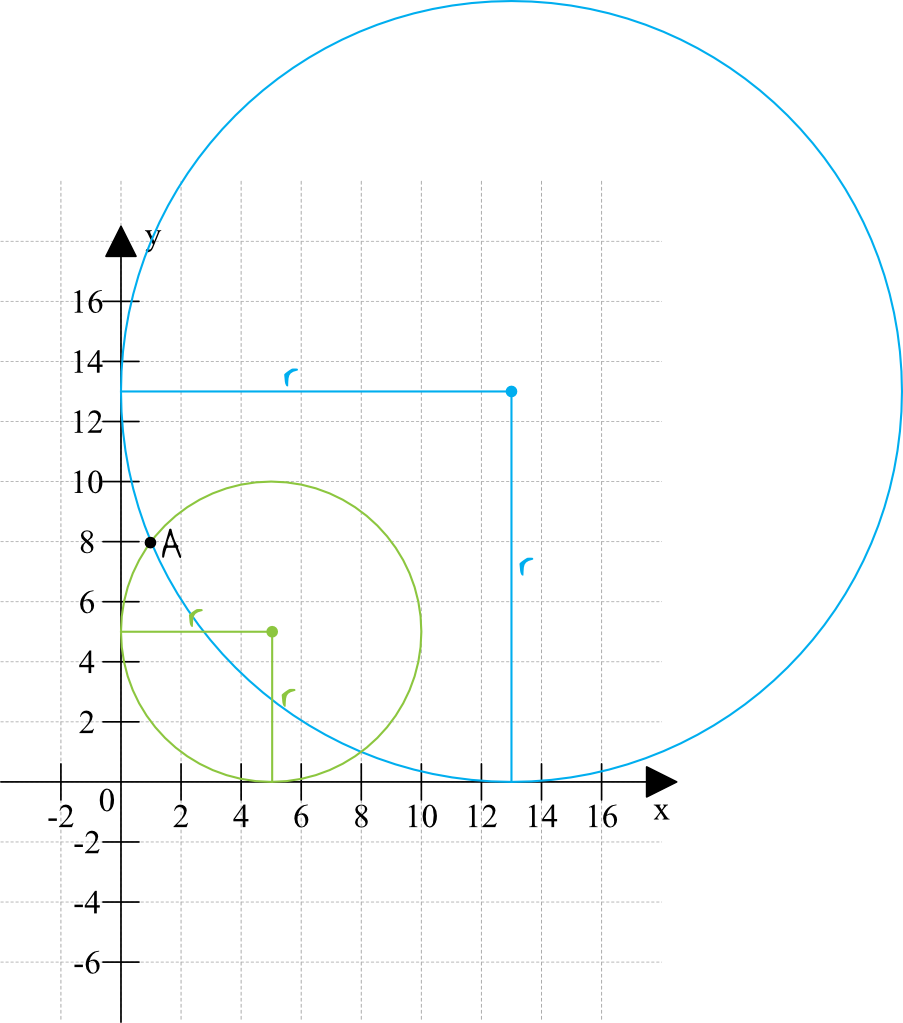
Co z tego rysunku możemy odczytać?
- będą dwa okręgi, które spełnią warunki zadania (aczkolwiek jakbyśmy dostrzegli tylko jeden okrąg, to nic się złego nie stanie, bo wszystko wyjdzie w trakcie obliczeń)
- na pewno te nasze okręgi znajdą się w pierwszej ćwiartce układu współrzędnych
- zarówno w przypadku mniejszego jak i większego okręgu odległości od osi iksów i igreków są równe długości promieni tych okręgów. Skoro tak, to możemy zapisać że współrzędne środka każdego z tych okręgów będą przybierać postać typu \(S=(r;r)\).
Krok 2. Podstawienie współrzędnych punktu \(A=(1;8)\) do wzoru na równanie okręgu.
Z tablic matematycznych możemy odczytać, że wzór na równanie okręgu o środku w punkcie \(S=(a;b)\) oraz promieniu \(r\) ma postać:
$$(x-a)^2+(y-b)^2=r^2$$
Ustaliliśmy już, że środek naszego okręgu ma współrzędne \(S=(r;r)\), czyli możemy całość zapisać jako:
$$(x-r)^2+(y-r)^2=r^2$$
Podstawmy teraz do tego wzoru współrzędne punktu \(A=(1;8)\), czyli \(x=1\) oraz \(y=8\). Otrzymamy w ten sposób:
$$(1-r)^2+(8-r)^2=r^2 \\
1-2r+r^2+64-16r+r^2=r^2 \\
2r^2-18r+65=r^2 \\
r^2-18r+65=0$$
Krok 3. Obliczenie powstałego równania kwadratowego.
Powstało nam równanie kwadratowe, które obliczymy korzystając z delty.
Współczynniki: \(a=1,\;b=-18,\;c=65\)
$$Δ=b^2-4ac=(-18)^2-4\cdot1\cdot65=324-260=64 \\
\sqrt{Δ}=\sqrt{64}=8$$
$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-18)-8}{2\cdot1}=\frac{18-8}{2}=\frac{10}{2}=5 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-18)+8}{2\cdot1}=\frac{18+8}{2}=\frac{26}{2}=13$$
Krok 4. Zapisanie równań okręgów przechodzących przez wskazany punkt.
Z obliczeń wyszły nam dwie możliwości długości promienia: \(r=5 \lor r=13\). Obydwie możliwości są poprawne, żadnej z nich nie odrzucamy (odrzucilibyśmy gdyby np. jedna z nich była ujemna). To oznacza, że warunki naszego zadania spełniają dwa okręgi (czyli tak jak wynikało to z rysunku szkicowego). Musimy już teraz tylko zapisać równania tych okręgów, pamiętając o tym że współrzędne środka okręgów są równe długości promienia:
Okrąg mniejszy: \((x-5)^2+(y-5)^2=5^2\), czyli \((x-5)^2+(y-5)^2=25\)
Okrąg większy: \((x-13)^2+(y-13)^2=13^2\), czyli \((x-13)^2+(y-13)^2=169\)