Egzamin gimnazjalny 2006 - matematyka
Egzamin zawiera 10 zadań zamkniętych oraz 4 zadania otwarte. Do zdobycia jest 25 punktów.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
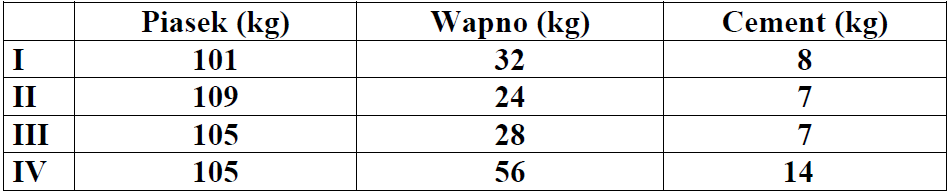
Zadanie 1. (1pkt) Aby przygotować suchą zaprawę do tynkowania ścian, należy zmieszać piasek, wapno i cement odpowiednio w stosunku \(15:4:1\). W którym wierszu tabeli podane są właściwe ilości składników potrzebnych do otrzymania \(140kg\) takiej zaprawy?
Zadanie 2. (1pkt) Na trójkątnym trawniku zamontowano obrotowy zraszacz. Aby podlać jak największą powierzchnię trawnika, nie oblewając jednocześnie ścieżek, należy ustawić zraszacz w punkcie przecięcia:
Zadanie 3. (1pkt) Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma \(144cm\). Jeśli przez \(x\) oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie:
Zadanie 4. (1pkt) Przez \(3\) godziny Jacek z Magdą obserwowali ruch samochodowy na moście. Liczyli przejeżdżające pojazdy. Wyniki zapisali w tabeli.
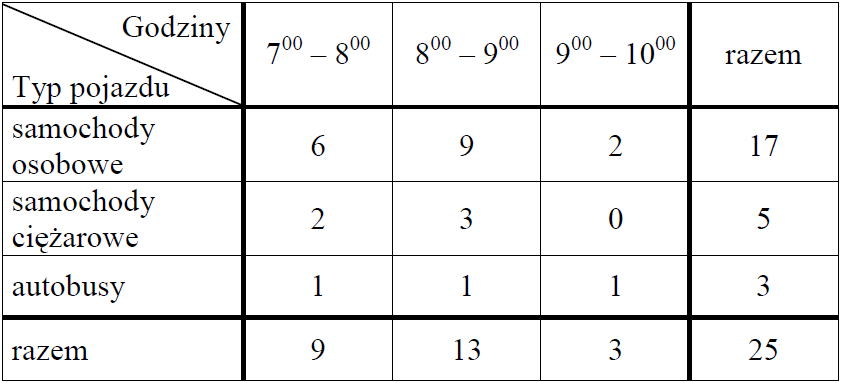
Który diagram przedstawia procentowy rozkład liczb pojazdów poszczególnych typów przejeżdżających przez most między \(700\) a \(800\)?

Zadanie 5. (1pkt) Przez \(3\) godziny Jacek z Magdą obserwowali ruch samochodowy na moście. Liczyli przejeżdżające pojazdy. Wyniki zapisali w tabeli.

Które zdanie wynika z danych w tabeli?
Zadanie 6. (1pkt) Przez \(3\) godziny Jacek z Magdą obserwowali ruch samochodowy na moście. Liczyli przejeżdżające pojazdy. Wyniki zapisali w tabeli.

Ile procent liczby wszystkich pojazdów, które przejechały przez most między 7:00 a 10:00, stanowi liczba samochodów osobowych?
Zadanie 7. (1pkt) Przez \(3\) godziny Jacek z Magdą obserwowali ruch samochodowy na moście. Liczyli przejeżdżające pojazdy. Wyniki zapisali w tabeli.

Ile samochodów osobowych przejeżdżało średnio przez most w ciągu jednej godziny obserwacji?
Zadanie 8. (1pkt) Wykres ilustruje zmiany temperatury gleby w pewnej miejscowości na głębokości \(10cm\) i \(30cm\) w ciągu doby w okresie lata.
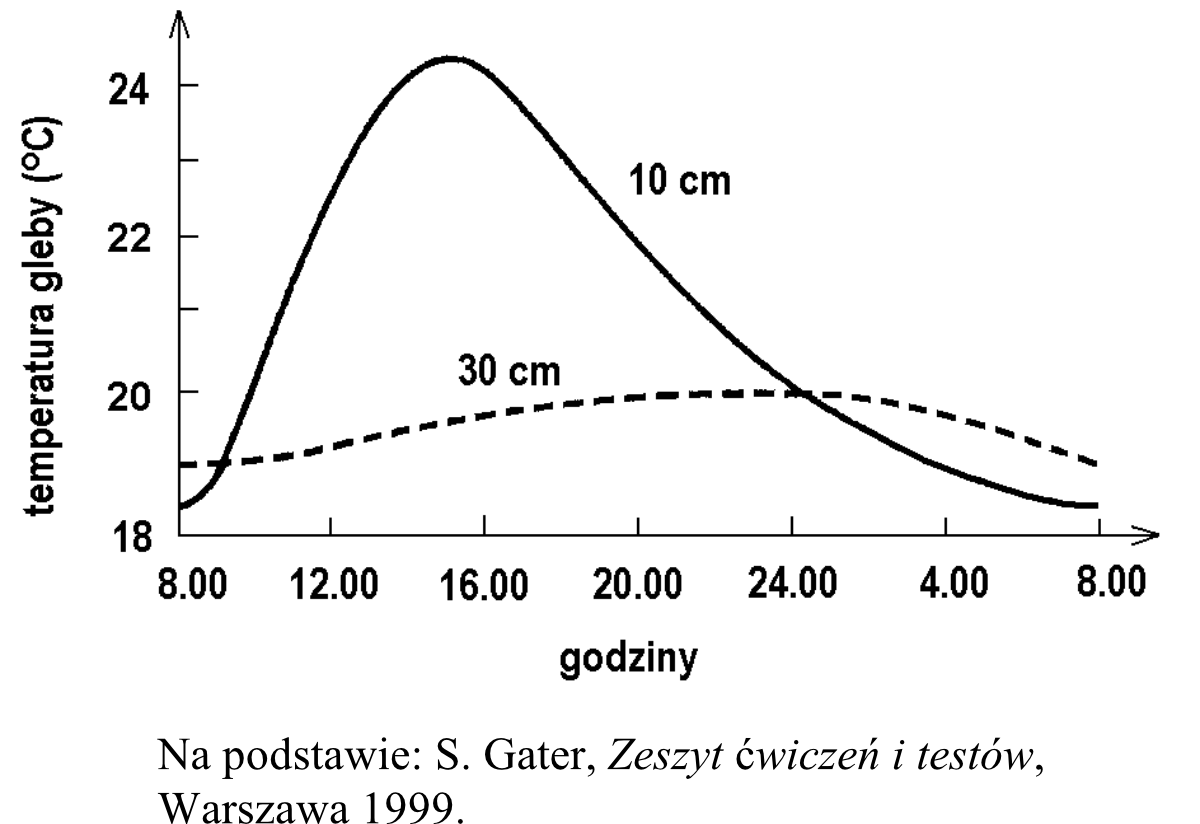
Z analizy wykresu wynika, że:
Zadanie 9. (1pkt) Wykres ilustruje zmiany temperatury gleby w pewnej miejscowości na głębokości \(10cm\) i \(30cm\) w ciągu doby w okresie lata.

Jaką temperaturę ma gleba w południe na głębokości \(10cm\)?
Zadanie 10. (1pkt) Wykres ilustruje zmiany temperatury gleby w pewnej miejscowości na głębokości \(10cm\) i \(30cm\) w ciągu doby w okresie lata.

Gleba na głębokości \(10cm\) ma najwyższą temperaturę około godziny:
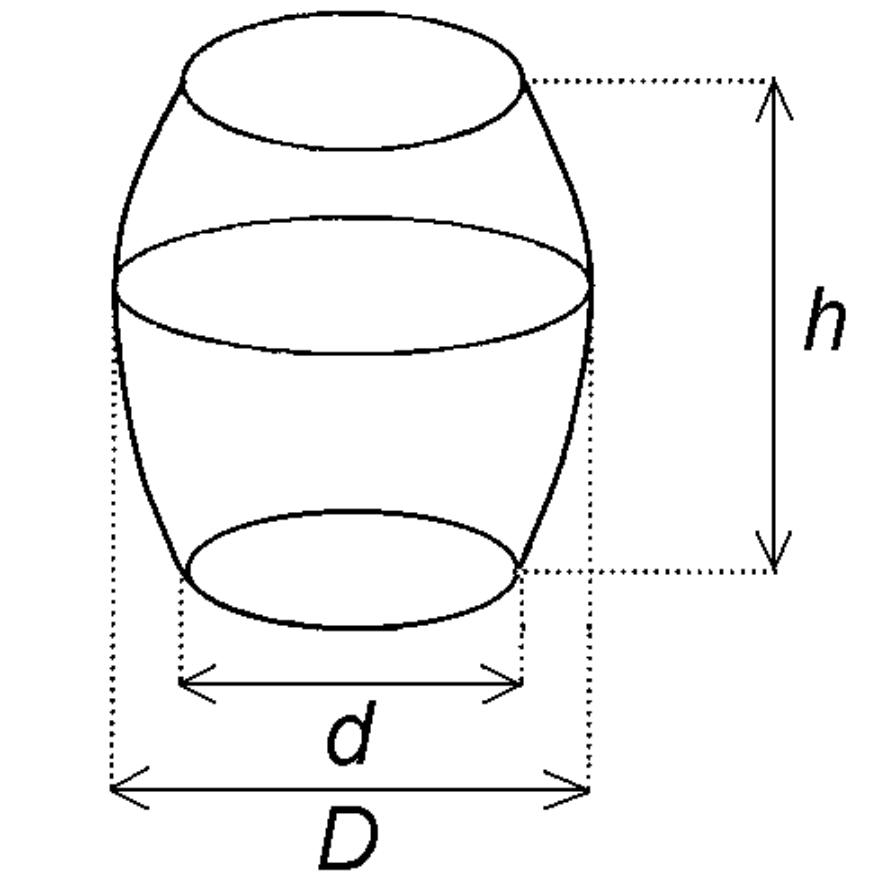
Zadanie 11. (4pkt) Objętość beczki oblicza się wg wzoru: \(V=\frac{1}{12}\cdot π\cdot(2D^2+d^2)\cdot h\), gdzie:
\(D\) - średnica w miejscu najszerszym
\(d\) - średnica dna
\(h\) - wysokość beczki
Wojtek obmierzył beczkę w ogrodzie. Ma ona wysokość \(12dm\) i średnicę dna równą \(7dm\). Z powodu trudności ze zmierzeniem średnicy w najszerszym miejscu Wojtek zmierzył obwód w najszerszym miejscu. Jest on równy \(33dm\). Oblicz objętość beczki. Dla ułatwienia obliczeń przyjmij \(π=\frac{22}{7}\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wykorzystując wzór na obwód okręgu zapiszesz, że \(r=\frac{33dm}{2π}\) (Krok 2.).
2 pkt
• Gdy obliczysz średnicę (nie promień!) beczki \(D=10,5dm\) (Krok 2.).
3 pkt
• Gdy podstawisz do wzoru z treści zadania obliczoną średnicę beczki (Krok 3.), ale otrzymasz niepoprawny wynik z powodu błędu rachunkowego.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wypisanie danych z treści zadania.
Stosując proponowane oznaczenia możemy zapisać, że:
\(d=7dm\)
\(h=12dm\)
\(Obw=33dm\) (obwód beczki w najszerszym miejscu)
Przyglądając się wzorowi zapisanemu na początku zadania widzimy, że brakuje nam znajomości długości \(D\), czyli średnicy w miejscu najszerszym. Do jej wyznaczenia wykorzystamy obwód beczki w jej najszerszym miejscu.
Krok 2. Obliczenie średnicy w miejscu najszerszym (\(D\)).
Wykorzystamy tutaj wzór na obwód okręgu:
$$Obw=2πr$$
Podstawiając dane do tego wzoru otrzymamy:
$$33dm=2πr \\
r=\frac{33dm}{2π} \\
r=\frac{33dm}{2\cdot\frac{22}{7}} \\
r=\frac{33dm}{\frac{44}{7}} \\
r=33dm\cdot\frac{7}{44} \\
r=5\frac{1}{4}dm$$
To jeszcze nie jest koniec, bo w ten sposób obliczyliśmy promień okręgu (tak naprawdę jest to promień przekroju poprzecznego beczki w jej najszerszym miejscu), a my potrzebujemy znać długość średnicy (czyli naszego \(D\)). Średnica jest dwukrotnie większa od promienia, zatem:
$$D=2\cdot r \\
D=2\cdot5\frac{1}{4}dm \\
D=10,5dm$$
Krok 3. Obliczenie objętości beczki.
Mamy już wszystkie potrzebne dane, więc możemy bez przeszkód obliczyć objętość naszej beczki, wykorzystując wzór z treści zadania:
$$\require{cancel}
V=\frac{1}{\cancel{12}}\cdot π\cdot(2\cdot(10,5)^2+(7)^2)\cdot\cancel{12} \\
V=(2\cdot110,25+49)π \\
V=(220,5+49)π \\
V=269,5π \\
V=269,5\cdot\frac{22}{7} \\
V=847[dm^3]$$
Zadanie 12. (3pkt) Wilgotnością drewna nazywamy stosunek masy wody zawartej w drewnie do masy drewna całkowicie suchego. Przyjęto podawać wilgotność drewna w procentach. Ich liczbę \((w)\) obliczamy za pomocą wzoru: \(w=\frac{M-m}{m}\cdot100\), gdzie:
- \(M\) oznacza masę drewna wilgotnego
- \(m\) oznacza masę drewna całkowicie suchego
Wyznacz \(M\) w zależności od \(m\) i \(w\). Zapisz kolejne przekształcenia wzoru.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy doprowadzisz równanie do postaci \(wm=(M-m)\cdot100\) i dalej popełnisz błąd.
2 pkt
• Gdy doprowadzisz równanie do postaci \(\frac{wm}{100}=M-m\) i dalej popełnisz błąd.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Najprościej będzie rozpocząć przekształcenie od pozbycia się postaci ułamkowej. Stąd też na początku najłatwiej jest cały wzór wymnożyć przez \(m\):
$$w=\frac{M-m}{m}\cdot100 \quad\bigg/\cdot m \\
wm=(M-m)\cdot100 \quad\bigg/:100 \\
\frac{wm}{100}=M-m \\
M=\frac{wm}{100}+m$$
Zadanie 13. (4pkt) Rysunek przedstawia szkic przekroju dachu dwuspadowego. Wysokość dachu \(GC=5,4m\), a szerokość podstawy \(AB=14,4m\). Oblicz długość krokwi \(AC\) i długość belki \(DE\), wiedząc, że odległość belki od podstawy dachu jest równa \(2,4m\) (czyli \(FG=2,4m)\).
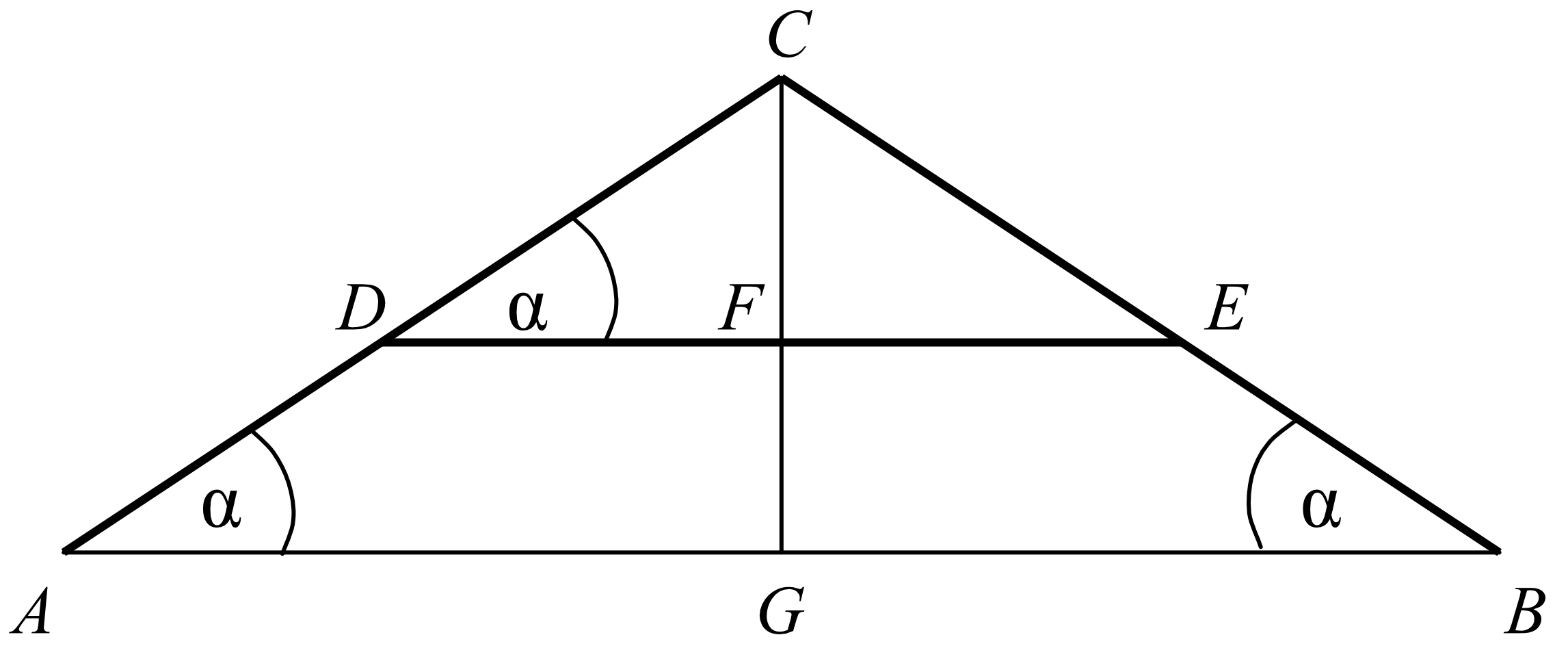
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość odcinka \(AC\) (Krok 1.).
2 pkt
• Gdy dostrzeżesz podobieństwo trójkątów \(ABC\) oraz \(DEC\) i zapiszesz poprawną proporcję np. \(\frac{|AC|}{|DC|}=\frac{|AB|}{|DE|}\) (Krok 2.).
3 pkt
• Gdy obliczysz długość odcinka \(DE\), ale otrzymany wynik nie jest prawidłowy z powodu błędów rachunkowych.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie długości odcinka \(AC\).
Aby obliczyć długość odcinka \(AC\) będziemy musieli posłużyć się Twierdzeniem Pitagorasa i trójkątem \(AGC\). Odcinek \(GC\) jest znany i jego długość wynosi \(5,4m\). Potrzebowalibyśmy poznać długość jeszcze odcinka \(AG\) i ona choć nie jest podana wprost, to jest prosta do wyznaczenia, bowiem będzie to połowa długości odcinka \(AB\). Skoro \(AB\) ma długość \(14,4m\), to odcinek \(AG\) ma długość \(14,4m:2=7,2m\). Zatem:
$$(7,2)^2+(5,4)^2=|AC|^2 \\
51,84+29,16=|AC|^2 \\
|AC|^2=81 \\
|AC|=9[m]$$
Krok 2. Obliczenie długości odcinka \(DE\).
Należy zauważyć, że trójkąty \(ABC\) oraz \(DEC\) są podobne (cecha podobieństwa: kąt-kąt-kąt). Skoro tak, to możemy poznać długość boku \(DE\) korzystając z proporcji w stylu:
$$\frac{|AC|}{|DC|}=\frac{|AB|}{|DE|} \\
\frac{9}{5}=\frac{14,4}{|DE|}$$
Mnożąc na krzyż otrzymamy:
$$9\cdot|DE|=72 \\
|DE|=8[m]$$
To oznacza, że mamy obliczone wszystko co było wymagane - długość krokwi \(AC\) wynosi \(9m\), natomiast długość belki \(DE\) jest równa \(8m\).
Uwaga: to nie była jedyna słuszna proporcja którą można zastosować. Równie dobrze można przykładowo zapisać proporcję:
$$\frac{AB}{DE}=\frac{CG}{CF}$$
Powyższa proporcja jest także jak najbardziej poprawna proporcja, tylko trzeba dodatkowo obliczyć długość odcinka \(CF\), a będzie ona równa \(5,4-2,4=3\).
Zadanie 14. (4pkt) Uzupełnij rachunek wystawiony przez firmę budowlaną, wpisując w wykropkowanych miejscach obliczone wartości.

Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie obliczysz jedną z brakujących wartości w tabeli.
2 pkt
• Gdy poprawnie obliczysz dwie z brakujących wartości w tabeli.
3 pkt
• Gdy poprawnie obliczysz trzy z brakujących wartości w tabeli.
4 pkt
• Gdy poprawnie obliczysz wszystkie brakujące wartości w tabeli.
Wyjaśnienie:
Krok 1. Obliczenie wartości podatku VAT za okno.
Pierwszą rubryczką do uzupełnienia jest podatek VAT za okno. Stanowi on \(22\%\) ceny netto, zatem będzie on równy:
$$0,22\cdot1200zł=264zł$$
Krok 2. Obliczenie całkowitej kwoty za okno.
Potrzebujemy teraz uzupełnić rubryczkę "Razem" za okno, która tak naprawdę będzie kwotą brutto. Musimy więc do ceny netto dodać wartość podatku VAT, zatem:
$$1200zł+264zł=1464zł$$
Krok 3. Obliczenie ceny netto za drzwi.
Aby lepiej zrozumieć ideę obliczania ceny netto wprowadźmy sobie proste oznaczenia:
\(x\) - cena netto drzwi
\(0,22x\) - wartość podatku VAT
Cena drzwi plus wartość podatku VAT ma nam dać kwotę brutto, czyli \(3538zł\). Możemy zatem zapisać, że:
$$x+0,22x=3538zł \\
1,22x=3538zł \\
x=2900zł$$
Cena netto drzwi jest więc równa \(2900zł\).
Krok 4. Obliczenie podatku VAT za drzwi.
Znając już cenę netto za drzwi bez problemu obliczymy należny podatek VAT:
$$0,22\cdot2900zł=638zł$$
Można też byłoby od ceny brutto odjąć cenę netto:
$$3538zł-2900zł=638zł$$