Próbny egzamin ósmoklasisty z matematyki - Operon 2019
Arkusz zawiera 15 zadań zamkniętych oraz 6 zadań otwartych. Łącznie do zdobycia jest 30 punktów, a sugerowany maksymalny czas rozwiązywania to około 100 minut.
W przypadku zadań zamkniętych musisz zaznaczyć daną odpowiedź klikając w odpowiedni przycisk. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak aby móc jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Jakim ułamkiem liczby \(3,5\) jest liczba \(5\)?
Zadanie 2. (1pkt) Dane jest wyrażenie \((2x-3)(x+3)-(x-1)^2\). Po doprowadzeniu do najprostszej postaci danego wyrażenia otrzymamy:
Zadanie 3. (1pkt) Dane jest równanie \(\frac{x}{2}+1=\frac{x}{3}\). Jaka liczba jest rozwiązaniem tego równania?
Zadanie 4. (1pkt) Czy liczby \(216\) i \(621\) są wielokrotnościami tej samej nieparzystej liczby dwucyfrowej?
Zadanie 5. (1pkt) W tabeli podano trzy wyrażenia.
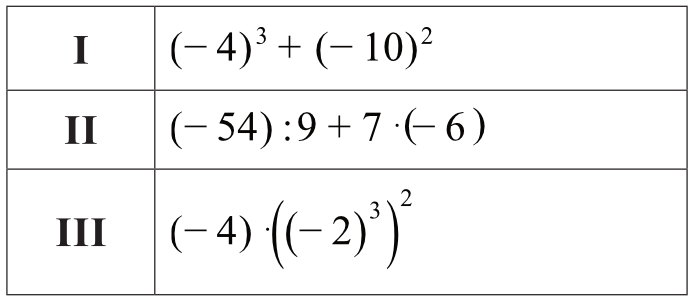
Które wyrażenia z tabeli mają wartość ujemną?
Zadanie 6. (1pkt) W pewnej szkole co szósty uczeń klasy ósmej deklaruje, że będzie kontynuował edukację w technikum. W tej szkole jest \(21\) takich uczniów.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Do danej szkoły uczęszcza \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\) uczniów klas ósmych.
Uczniowie, którzy chcą się uczyć w technikum, stanowią \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\) niż \(20\%\) wszystkich ósmoklasistów tej szkoły.
Zadanie 7. (1pkt) Blokada rowerowa ma zapięcie z szyfrowanym zamkiem z trzema zapadkami. Na każdej z zapadek można ustawić cyfry od \(0\) do \(9\). Szyfr otwierający zamek tej blokady tworzą trzy cyfry, które są kolejnymi liczbami parzystymi.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F - jeśli jest fałszywe.
Prawdopodobieństwo, że pierwszą cyfrą szyfru jest cyfra \(0\), wynosi \(\frac{1}{9}\).
Istnieją trzy możliwości wyboru szyfru dla zamka w takiej blokadzie.
Zadanie 8. (1pkt) Wartość wyrażenia \(3a-a^2\) dla \(a=\sqrt{5}\) w przybliżeniu do całości jest równa:
Zadanie 9. (1pkt) Jeśli Kamil jedzie rowerem ze średnią prędkością \(18\frac{km}{h}\), a Agata na hulajnodze elektrycznej pokonuje każde \(400m\) w ciągu minuty, to znaczy, że:
Zadanie 10. (1pkt) Dany jest kwadrat o polu powierzchni \(48cm^2\). Ile wynosi długość przekątnej tego kwadratu?
Zadanie 11. (1pkt) Dany jest trapez \(KLMN\), w którym boki \(LM\) i \(MN\) są przystające, a przekątna \(LN\) jest prostopadła do boku \(KN\).
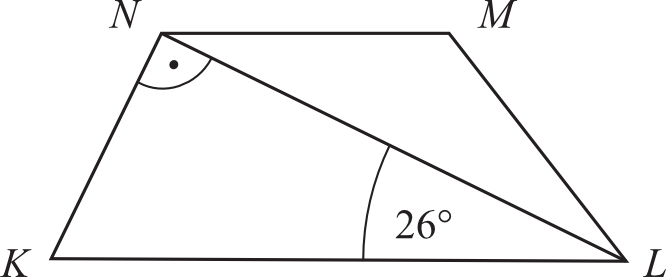
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F - jeśli jest fałszywe.
Kąt ostry \(NKL\) ma miarę \(64°\).
Trapez \(KLMN\) jest trapezem równoramiennym.
Zadanie 12. (1pkt) Prostokąt przedstawiony na rysunku został częściowo pomalowany.
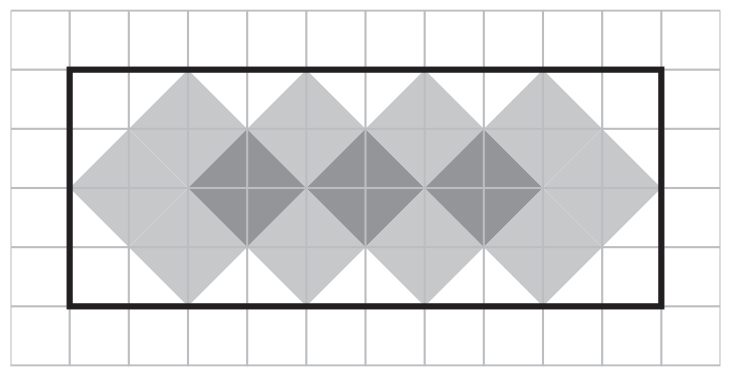
Jaki procent prostokąta został pomalowany?
Zadanie 13. (1pkt) Kolejne liczby wstawiono do poniższej tabeli w pewien uporządkowany sposób. W przedstawionej tabeli brakuje jednej liczby.

Jakiej liczby brakuje w tabeli?
Zadanie 14. (1pkt) Wykres przedstawia temperatury w stopniach Celsjusza, jakie odnotowano w wybranym tygodniu lipca. Temperatura w sobotę wynosiła tyle, ile średnia temperatura z pozostałych dni tygodnia. Jaką temperaturę odnotowano w danym tygodniu w sobotę?

Zadanie 15. (1pkt) Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Na mapie, która pomniejsza \(600\) tys. razy, rzeczywista odległość \(150km\) będzie odcinkiem o długości \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\).
Na planie wykonanym w skali \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\) budynek o rzeczywistej długości \(28m\) to odcinek o długości \(3,5cm\).
Zadanie 16. (2pkt) W prostokątnym układzie współrzędnych dane są dwa punkty: \(A=(-1;-2)\) i \(B=(2;1)\).
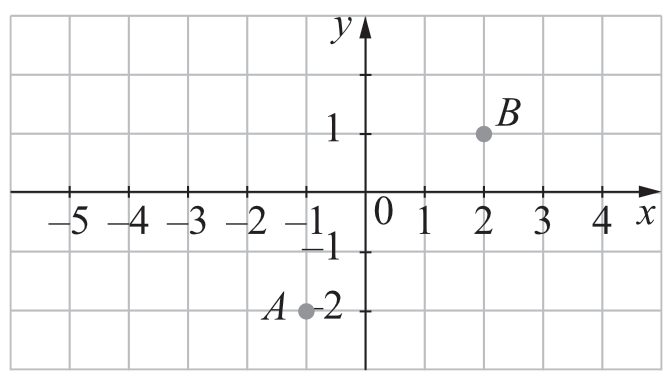
Czy punkt \(B\) leży w kole o środku w punkcie \(A\) i promieniu \(r=4\)? Odpowiedź uzasadnij.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość odcinka \(AB\).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Obliczenie długości odcinka \(AB\).
Aby dowiedzieć się, czy punkt \(B\) należy do koła, to musimy sprawdzić jaka jest odległość od punktu \(A\) do punktu \(B\). Jeżeli ta odległość jest mniejsza lub równa promieniowi koła, to punkt \(B\) będzie leżeć w kole. Jeżeli ta odległość jest większa od długości promienia, to punkt \(B\) będzie poza kołem.
Aby obliczyć długość odcinka \(AB\) możemy skorzystać z Twierdzenia Pitagorasa:
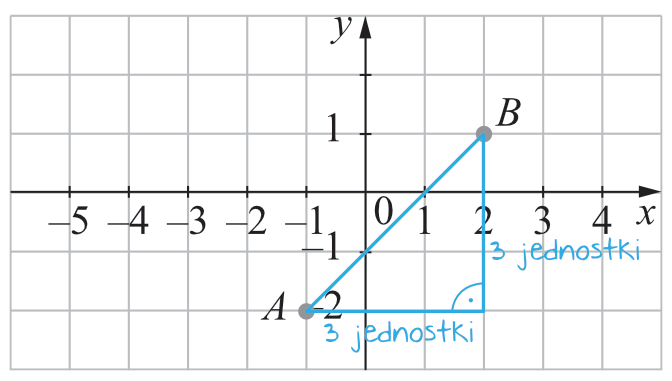
Nasz odcinek \(AB\) jest przeciwprostokątną trójkąta o przyprostokątnych równych \(3\), zatem:
$$3^2+3^2=|AB|^2 \\
9+9=|AB|^2 \\
|AB|^2=18 \\
|AB|=\sqrt{18} \quad\lor\quad |AB|=-\sqrt{18}$$
Ujemną długość oczywiście odrzucamy, bo długość odcinka jest na pewno dodatnia, zatem wiemy już, że \(AB=\sqrt{18}\). Na upartego moglibyśmy jeszcze wyłączyć czynnik przez znak pierwiastka i zapisać, że \(AB=3\sqrt{2}\), ale nie jest to konieczne, bo postać \(\sqrt{18}\) będzie dla nas za chwilę bardzo pożyteczna.
Krok 2. Ustalenie, czy punkt \(B\) leży w kole.
Promień naszego koła to \(r=4\). Odległość od punktu \(A\) do punktu \(B\) wynosi \(\sqrt{18}\). Powinniśmy dostrzec, że \(\sqrt{18}\) jest na pewno większy od \(4\). Skąd to wiemy? Po prostu \(\sqrt{16}=4\), więc \(\sqrt{18}\) musi być większy od \(4\). To oznacza, że punkt \(B\) znajduje się poza kołem.
Zadanie 17. (2pkt) W prostokącie o obwodzie \(98cm\) stosunek długości sąsiednich boków wynosi \(2:5\). Oblicz pole tego prostokąta.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy rozwiążesz całe zadanie, ale otrzymasz błędny wynik jedynie ze względu na błędy rachunkowe.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wprowadzenie oznaczeń i zapisanie równania.
Skoro stosunek długości sąsiednich boków wynosi \(2:5\), to możemy wprowadzić do zadania następujące oznaczenia:
\(2x\) - długość krótszego boku
\(5x\) - długość dłuższego boku
Obwód prostokąta wyliczamy dodając przez siebie długości wszystkich boków, zatem:
$$2\cdot2x+2\cdot5x=98$$
Krok 2. Obliczenie długości boków prostokąta.
Powstało nam proste równanie liniowe, które musimy teraz rozwiązać:
$$2\cdot2x+2\cdot5x=98 \\
4x+10x=98 \\
14x=98 \\
x=7[cm]$$
Teraz musimy spojrzeć na nasze oznaczenia i obliczyć długości poszczególnych boków. Krótszy bok ma długość \(2x\), czyli będzie miał on \(2\cdot7cm=14cm\). Dłuższy bok ma długość \(5x\), czyli będzie to \(5\cdot7cm=35cm\).
Krok 3. Obliczenie pola powierzchni prostokąta.
Na sam koniec musimy obliczyć jeszcze pole powierzchni prostokąta, zatem:
$$P=ab \\
P=14cm\cdot35cm \\
P=490cm^2$$
Zadanie 18. (2pkt) W kole narysowano cięciwę o długości \(10cm\), a jej końce połączono odcinkami ze środkiem koła, tak że powstał trójkąt, którego jeden z kątów ma miarę \(120°\). Oblicz, jaką długość ma promień tego koła.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy rozwiążesz całe zadanie, ale otrzymasz błędny wynik jedynie ze względu na błędy rachunkowe.
ALBO
• Gdy zamiast promienia okręgu obliczysz wysokość trójkąta \(h=\frac{5}{\sqrt{3}}\) lub \(h=\frac{5\sqrt{3}}{3}\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Zanim zaczniemy liczyć, to narysujmy sobie szkic tej całej sytuacji, zaznaczając przy okazji kluczowy kąt \(120°\):
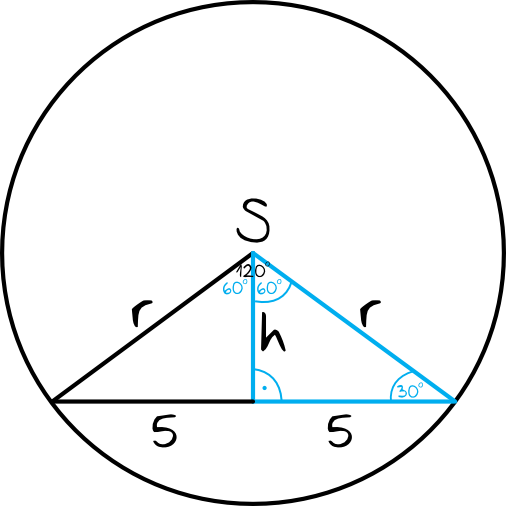
Zwróćmy uwagę na to, że powstał nam trójkąt prostokątny o kątach \(30°,60°,90°\). To właśnie on będzie kluczem do rozwiązania tego zadania. Musimy też zauważyć, że dolna przyprostokątna ma długość \(5\), bowiem w trójkątach równoramiennych wysokość dzieli nam podstawę na dwie równe części, a podstawa była równa \(10\).
Krok 2. Obliczenie promienia koła.
Korzystając z własności trójkątów o kątach \(30°,60°,90°\) wiemy, że jeżeli przyprostokątna leżąca przy kącie \(60°\) ma długość \(a\), to druga przyprostokątna ma długość \(a\sqrt{3}\), a przeciwprostokątna ma długość \(2a\).
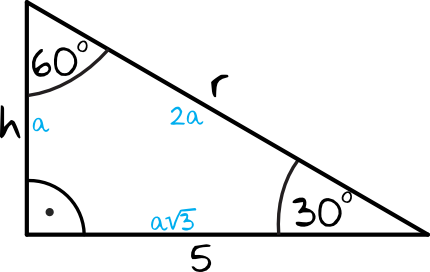
Zgodnie z naszymi oznaczeniami widzimy, że dolna przyprostokątna ma długość \(5\), zatem:
$$a\sqrt{3}=5 \\
a=\frac{5}{\sqrt{3}}$$
Nas interesuje długość przeciwprostokątnej, czyli długość \(2a\). W związku z tym:
$$r=2a=2\cdot\frac{5}{\sqrt{3}}=\frac{10}{\sqrt{3}}$$
Otrzymana odpowiedź jest już poprawna, ale powinniśmy jeszcze usunąć niewymierność z mianownika, a zrobimy to mnożąc licznik i mianownik przez \(\sqrt{3}\), zatem:
$$r=\frac{10\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{10\sqrt{3}}{3}$$
Zadanie 19. (3pkt) Łączny koszt zakupu dwóch książek o różnych tytułach wynosił \(82zł\). Do biblioteki zakupiono po \(5\) sztuk każdej z nich w promocyjnej cenie o \(20\%\) niższej. Koszt zakupu pierwszego tytułu wyniósł \(152zł\). Oblicz cenę każdej z książek przed promocją.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz promocyjną cenę pojedynczego egzemplarza pierwszej książki (patrz: Krok 1.).
ALBO
• Gdy promocyjną cenę wszystkich książek, która wyniesie \(410zł\).
2 pkt
• Gdy obliczysz cenę pierwszej książki przed promocją (patrz: Krok 2.).
ALBO
• Gdy rozwiążesz całe zadanie, ale otrzymasz błędny wynik jedynie ze względu na błędy rachunkowe.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie ceny promocyjnej pierwszej książki.
Najpierw obliczmy promocyjną cenę pierwszej książki. Wiemy, że pięć książek zakupionych po promocyjnej cenie kosztuje \(152zł\). Skoro tak, to taka pojedyncza książka kosztuje:
$$152zł:5=30,40zł$$
Krok 2. Obliczenie ceny pierwszej książki (przed promocją).
Wiemy, że pierwszy tytuł w promocji kosztuje \(30,40zł\). Promocyjna cena jest o \(20\%\) niższa od początkowej. To oznacza, że cena promocyjna stanowi \(80\%\) ceny początkowej. Możemy więc ułożyć prostą proporcję:
Skoro \(80\%\) ceny początkowej jest równe \(30,40zł\)
To \(10\%\) ceny początkowej jest równe \(3,80zł\)
Więc \(100\%\) ceny początkowej jest równe \(38zł\)
Ewentualnie moglibyśmy przyjąć, że \(x\) to początkowa cena pierwszej książki i zapisać, że:
$$0,8x=30,40zł \\
x=38zł$$
Krok 3. Obliczenie ceny drugiej książki (przed promocją).
Wiemy już, że pierwsza książka kosztuje \(38zł\). Koszt zakupu pierwszej i drugiej książki wynosi \(82zł\), zatem druga książka kosztuje:
$$82zł-38zł=44zł$$
Zadanie 20. (3pkt) Firma remontowa otrzymała zlecenie na położenie nowych podłóg w dwóch mieszkaniach o łącznej powierzchni \(159m^2\). W pierwszym mieszkaniu wyłożono już \(24m^2\) nowej podłogi, co stanowi \(\frac{3}{8}\) powierzchni podłogi w tym mieszkaniu. W drugim natomiast pozostała jeszcze do położenia tylko podłoga w pokoju o wymiarach \(3,8m\times5m\). Czy firma położyła już podłogę na \(\frac{2}{3}\) powierzchni w obu mieszkaniach? Odpowiedź uzasadnij.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz powierzchnię podłóg pierwszego mieszkania (patrz: Krok 1.).
2 pkt
• Gdy obliczysz powierzchnię podłóg drugiego mieszkania (patrz: Krok 2.).
ALBO
• Gdy rozwiążesz całe zadanie, ale otrzymasz błędny wynik jedynie ze względu na błędy rachunkowe.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie pola powierzchni podłogi w pierwszym mieszkaniu.
Wiemy, że w pierwszym mieszkaniu wyłożono już \(24m^2\) nowej podłogi i że jest to \(\frac{3}{8}\) powierzchni podłogi całego mieszkania. Jeżeli więc oznaczymy sobie jako \(x\) pole powierzchni podłogi pierwszego mieszkania, to otrzymamy następujące równanie:
$$\frac{3}{8}x=24m^2 \\
\frac{1}{8}x=8m^2 \\
x=64m^2$$
Krok 2. Obliczenie pola powierzchni podłogi w drugim mieszkaniu.
Skoro suma podłóg w pierwszym i drugim mieszkaniu jest równa \(159m^2\), a nasze pierwsze mieszkanie ma \(64m^2\) podłóg, to drugie mieszkanie będzie mieć:
$$159m^2-64m^2=95m^2$$
Krok 3. Obliczenie pola powierzchni podłogi, która jest już wyłożona w pierwszym i drugim mieszkaniu.
Z treści zadania wiemy, że w pierwszym mieszkaniu wyłożono \(24m^2\) nowej podłogi. Policzmy teraz ile podłogi wyłożono w drugim mieszkaniu.
Wiemy, że w drugim mieszkaniu firmie remontowej zostało do wyłożenia \(3,8m\times5m\), czyli zostało im do wyłożenia:
$$3,8m\cdot5m=19m^2$$
Skoro całe mieszkanie ma \(95m^2\), a do wyłożenia zostało im \(19m^2\), to wyłożono już:
$$95m^2-19m^2=76m^2$$
To oznacza, że w pierwszym i drugim mieszkaniu wyłożono łącznie:
$$24m^2+76m^2=100m^2$$
Krok 4. Zakończenie zadania.
Pytają się nas, czy firma zdołała już wyłożyć podłogę na \(\frac{2}{3}\) powierzchni w obu mieszkaniach. Wiemy, że firma wyłożyła \(100m^2\) ze \(159m^2\), czyli wyłożyła \(\frac{100}{159}\) metrów kwadratowych podłogi. Ułamek \(\frac{100}{159}\) jest na pewno mniejszy od \(\frac{2}{3}\), bowiem \(\frac{2}{3}=\frac{100}{150}\) lub jak kto woli \(\frac{2}{3}=\frac{106}{159}\). To oznacza, że firma wyłożyła mniej niż \(\frac{2}{3}\) podłóg.
Zadanie 21. (3pkt) W ostrosłupie prostym podstawą jest romb o przekątnych \(10cm\) i \(24cm\). Wysokość ostrosłupa jest dwa razy dłuższa niż bok rombu. Oblicz objętość tego ostrosłupa.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość boku rombu (patrz: Krok 1.).
2 pkt
• Gdy rozwiążesz całe zadanie, ale otrzymasz błędny wynik jedynie ze względu na błędy rachunkowe.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie długości boku rombu.
Z własności rombów wiemy, że przekątne rombu przecinają się pod kątem prostym w połowie swojej długości. To oznacza, że otrzymamy następującą sytuację:
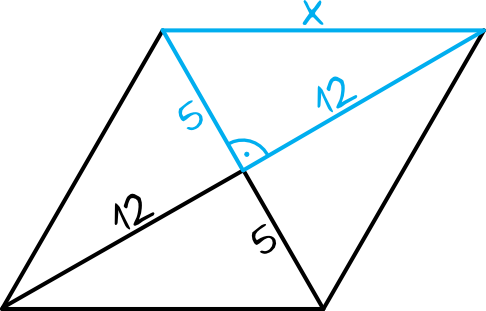
Powstały nam na rysunku trójkąty prostokątne z których możemy obliczyć długość boku rombu. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$5^2+12^2=x^2 \\
25+144=x^2 \\
x^2=169 \\
x=13 \quad\lor\quad x=-13$$
Bok rombu jest na pewno liczbą dodatnią, zatem zostaje nam \(x=13\).
Krok 2. Obliczenie wysokości ostrosłupa.
Z treści zadania wynika, że ostrosłup ma wysokość dwa razy dłuższą od boku rombu. Skoro więc bok rombu miał długość \(13cm\), to wysokość będzie równa:
$$H=2\cdot13cm \\
H=26cm$$
Krok 3. Obliczenie pola podstawy ostrosłupa.
Znamy długości przekątnych rombu, zatem możemy bez przeszkód obliczyć jego pole powierzchni, które jednocześnie będzie polem podstawy ostrosłupa:
$$P_{p}=\frac{1}{2}ef \\
P_{p}=\frac{1}{2}\cdot10\cdot24 \\
P_{p}=5\cdot24 \\
P_{p}=120[cm^2]$$
Krok 4. Obliczenie objętości ostrosłupa.
Wiemy już, że \(P_{p}=120cm^2\) oraz że \(H=26cm\), zatem objętość ostrosłupa będzie równa:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot120cm^2\cdot26cm \\
V=40cm^2\cdot26cm \\
V=1040cm^3$$