Egzamin gimnazjalny 2007 - matematyka
Egzamin zawiera 10 zadań zamkniętych oraz 4 zadania otwarte. Do zdobycia są 22 punkty.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Zasolenie morza określa się jako ilość gramów soli rozpuszczonych w jednym kilogramie wody morskiej i podaje w promilach \((‰)\). Przeciętnie w jednym kilogramie wody morskiej znajduje się \(34,5g\) różnych rozpuszczonych w niej soli (czyli przeciętne zasolenie wody morskiej jest równe \(34,5‰\). Zasolenie Bałtyku (średnio \(7,8‰\)) jest znacznie mniejsze od zasolenia oceanów, co tłumaczy się wielkością zlewiska (duży dopływ wód rzecznych), warunkami klimatycznymi (małe parowanie) oraz utrudnioną wymianą wód z oceanem. Jedna tona średnio zasolonej wody z Morza Bałtyckiego zawiera około:
Zadanie 2. (1pkt) Długość trasy na mapie w skali \(1:10\;000\;000\) jest równa \(7,7cm\). W rzeczywistości trasa ta ma długość:
Zadanie 3. (1pkt) Na rysunkach przedstawiono flagi sygnałowe Międzynarodowego Kodu Sygnałowego używanego do porozumiewania się na morzu.

Który z przedstawionych rysunków flag ma \(4\) osie symetrii?
Zadanie 4. (1pkt) Na rysunkach przedstawiono flagi sygnałowe Międzynarodowego Kodu Sygnałowego używanego do porozumiewania się na morzu.

Który z przedstawionych rysunków flag nie ma środka symetrii?
Zadanie 5. (1pkt) Poważnym problemem są zanieczyszczenia Bałtyku substancjami biogennymi. Diagramy przedstawiają procentowy udział państw nadbałtyckich w zanieczyszczeniu Morza Bałtyckiego związkami azotu (diagram a) i związkami fosforu (diagram b) w 1995 roku.
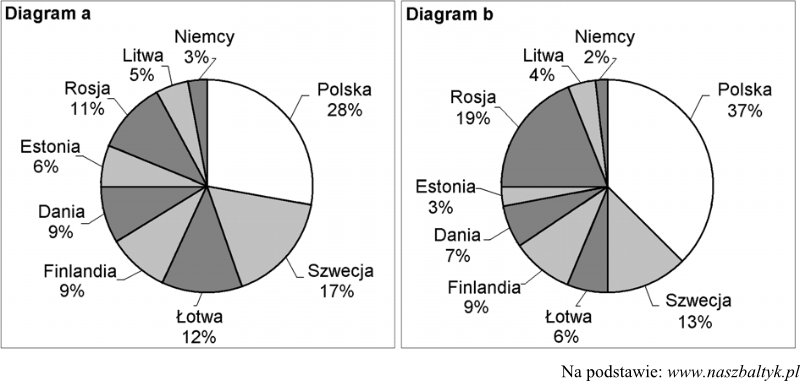
Procentowy udział Polski w zanieczyszczeniu Bałtyku związkami azotu w 1995r. był taki, jak łącznie krajów:
Zadanie 6. (1pkt) Poważnym problemem są zanieczyszczenia Bałtyku substancjami biogennymi. Diagramy przedstawiają procentowy udział państw nadbałtyckich w zanieczyszczeniu Morza Bałtyckiego związkami azotu (diagram a) i związkami fosforu (diagram b) w 1995 roku.

Czworo uczniów podjęło próbę ustalenia na podstawie diagramów, czy w 1995 roku do Bałtyku trafiło z obszaru Polski więcej ton związków azotu czy związków fosforu. Oto ich odpowiedzi:
Bartek - Trafiło więcej ton związków fosforu.
Ewa - Trafiło więcej ton związków azotu.
Tomek - Do Bałtyku trafiło tyle samo ton związków azotu co fosforu.
Hania - Nie można obliczyć, bo brakuje danych o masie zanieczyszczeń poszczególnymi związkami.
Kto odpowiedział poprawnie?
Zadanie 7. (1pkt) Rysunki przedstawiają wskazania wodomierza w dniach 1 września i 1 października.
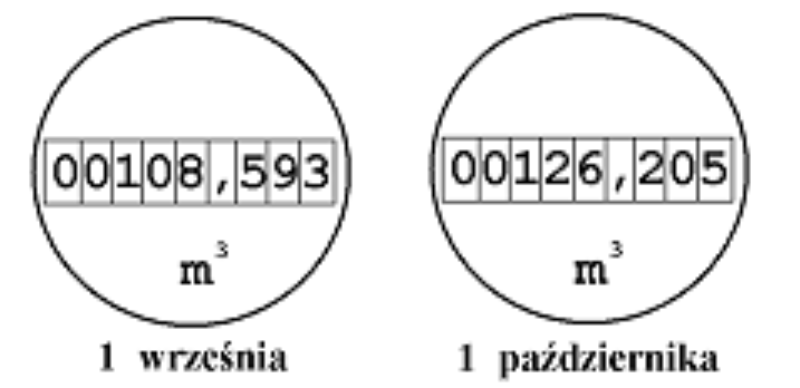
Oblicz, zaokrąglając do całości, ile metrów sześciennych wody zużyto od 1 września do 1 października.
Zadanie 8. (1pkt) Pierwszego października wodomierz wskazywał \(126,205m^3\). Jakie będzie wskazanie tego wodomierza po zużyciu kolejnych \(10\) litrów wody?
Zadanie 9. (1pkt) Objętość \((V)\) cieczy przepływającej przez rurę o polu przekroju \(S\) oblicza się według wzoru \(V=Sv_{c}t\), gdzie:
\(v_{c}\) - prędkość przepływu cieczy
\(t\) - czas przepływu
Który wzór na prędkość cieczy przepływającej przez rurę jest rezultatem poprawnego przekształcenia podanego wzoru?
Zadanie 10. (1pkt) Rodzice Jacka kupili \(36\) butelek wody mineralnej o pojemnościach \(0,5\) litra i \(1,5\) litra. W sumie zakupili \(42\) litry wody. Przyjmij, że \(x\) oznacza liczbę butelek o pojemności \(0,5\) litra, \(y\) - liczbę butelek o pojemności \(1,5\) litra. Który układ równań umożliwi obliczenie, ile zakupiono mniejszych butelek wody mineralnej, a ile większych?
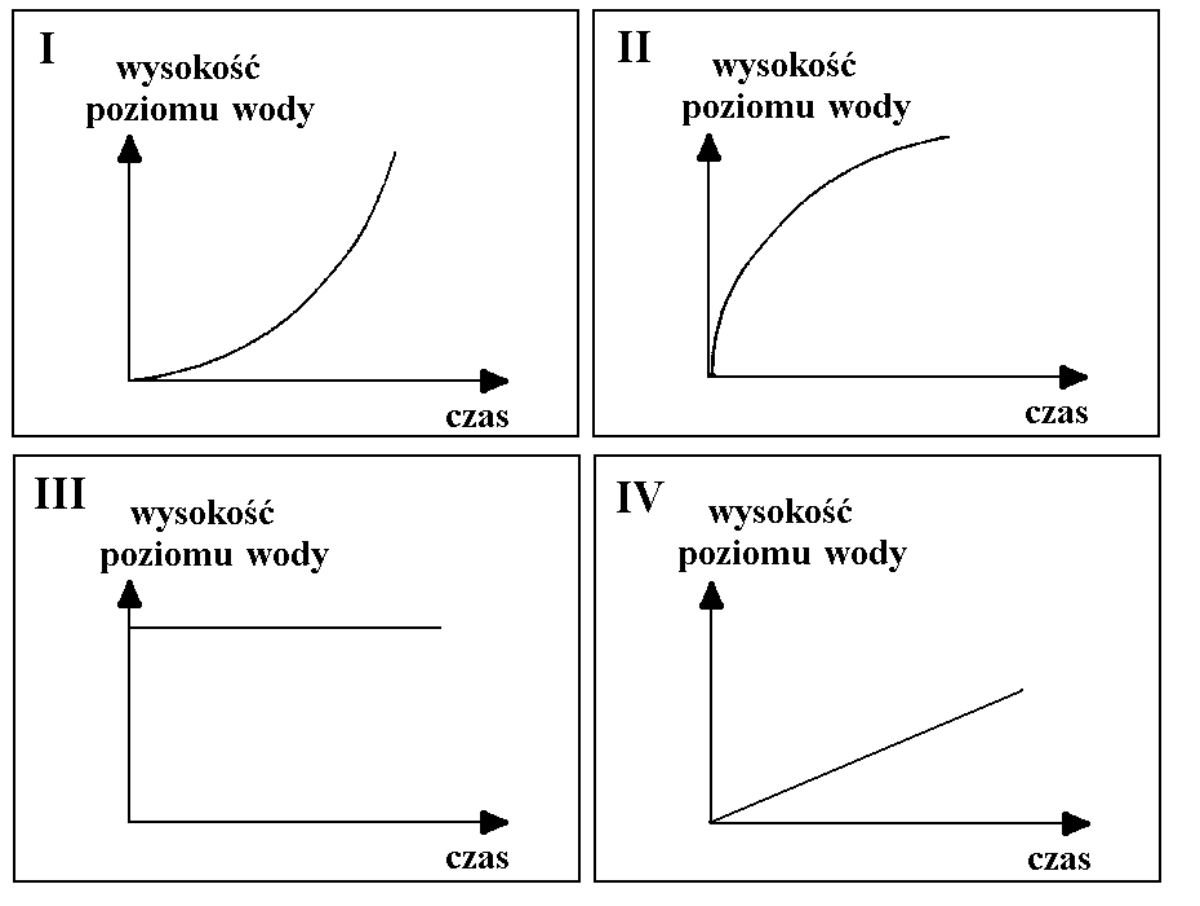
Zadanie 11. (2pkt) Do początkowo pustych wazonów, takich jak przedstawione na rysunkach, jednakowym i równomiernym strumieniem wpływała woda.
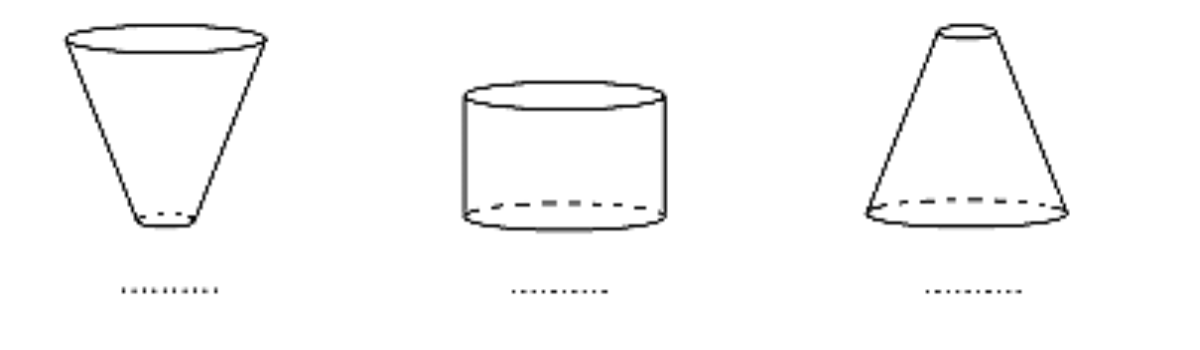
Na wykresach I-IV przedstawiono schematycznie charakter zależności wysokości poziomu wody w wazonie od czasu jego napełniania. Dopasuj odpowiedni wykres do każdego z wazonów.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie dopasujesz wykresy do dwóch wazonów.
2 pkt
• Gdy poprawnie dopasujesz wykresy do trzech wazonów.
Wyjaśnienie:
Krok 1. Ustalenie wykresu dla pierwszego wazonu.
Pierwszy wazon jest zwężony na dole, więc na początku wlewania bardzo szybko podniesie się poziom wody i z czasem będzie on przyrastał coraz wolniej. Taką sytuację mamy na II wykresie.
Krok 2. Ustalenie wykresu dla drugiego wazonu.
W drugim wazonie nie mamy żadnych zwężeń, wysokość poziomu wody będzie więc wzrastać liniowo, czyli dokładnie tak jak jest to na IV wykresie.
Krok 3. Ustalenie wykresu dla trzeciego wazonu.
Tutaj mamy sytuację odwrotną do pierwszego wazonu. Na początku słup wysokości wody będzie bardzo wolno wzrastał, bo na dole naczynie jest najszersze. Z czasem przyrost wysokości poziomu wody będzie coraz większy, zatem prawidłowym wykresem będzie w tym przypadku wykres pierwszy.
Zadanie 12. (2pkt) W wiadrze jest \(x\) litrów wody, a w garnku \(y\) litrów wody. Ile litrów wody będzie w wiadrze, a ile w garnku, jeśli:
a) z wiadra przelejemy do garnka \(1,5\) litra wody.
b) przelejemy połowę wody z garnka do wiadra.

Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie obliczysz ilość litrów wody w wiadrze i garnku w jednym z dwóch przypadków (Krok 1. lub 2.).
2 pkt
• Gdy poprawnie obliczysz ilość litrów wody w wiadrze i garnku w obydwu przypadkach (Krok 1. i 2.).
Wyjaśnienie:
Krok 1. Rozpatrzenie punktu pierwszego.
Jeżeli z wiadra przelewamy \(1,5\) litra wody, to w wiadrze będziemy mieć \(x-1,5\), natomiast w garnku przybędzie \(1,5\) litra, zatem znajdzie się tam teraz \(y+1,5\) litrów.
Krok 2. Rozpatrzenie punktu drugiego.
Musimy przelać połowę wody z garnka, czyli \(0,5y\) litrów. To oznacza, że w wiadrze znajdzie się \(x+0,5y\) litrów wody, natomiast w garnku zostanie \(y-0,5y=0,5y\) litrów wody.
Zadanie 13. (4pkt) Przekrój poprzeczny ziemnego wału przeciwpowodziowego ma mieć kształt równoramiennego trapezu o podstawach długości \(6m\) i \(16m\) oraz wysokości \(12m\). Trzeba jednak usypać wyższy wał, bo przez dwa lata ziemia osiądzie i wysokość wału zmniejszy się o \(20\%\) (szerokość wału u podnóża i na szczycie nie zmienia się).
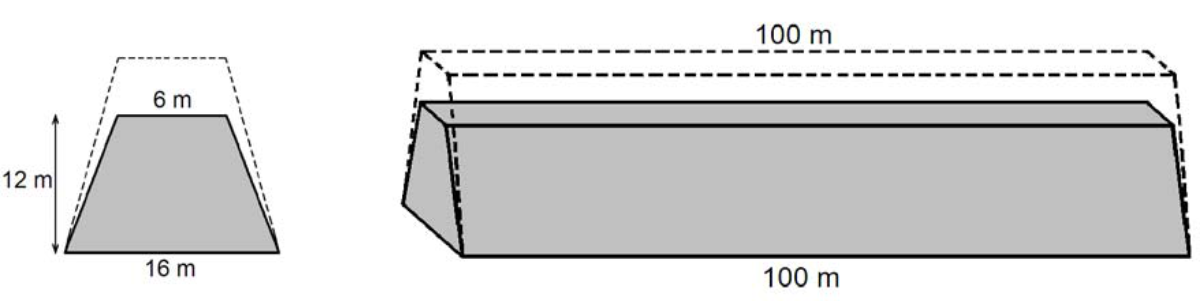
Oblicz, ile metrów sześciennych ziemi trzeba przywieźć na usypanie \(100\)-metrowego odcinka ziemnego wału przeciwpowodziowego (w kształcie graniastosłupa prostego) opisanego w informacjach.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz wysokość dużego (świeżo usypanego) wału (Krok 1.).
ALBO
• Gdy obliczysz pole powierzchni trapezu będącego przekrojem docelowego odcinka wału \(P=132m^2\).
2 pkt
• Gdy obliczysz pole powierzchni przekroju dużego wału (świeżo usypanego) (Krok 2.).
3 pkt
• Gdy obliczysz objętość wału (Krok 3.), ale otrzymany wynik jest niepoprawny z powodu błędu rachunkowego.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie wysokości dużego wału (świeżo usypanego).
Zgodnie z rysunkiem wiemy, że docelowy wał ma \(12m\) i że stanowić on będzie \(80\%\) tego co zostanie usypane. W związku z tym możemy zapisać następujące oznaczenia:
\(x\) - wysokość świeżo usypanego wału
\(0,8x\) - wysokość wału docelowego
Nasz wał docelowy ma \(12m\), czyli zajdzie równanie:
$$0,8x=12m \\
x=15m$$
To oznacza, że świeżo nasypany wał będzie mieć wysokość \(15m\).
Krok 2. Obliczenie pola powierzchni przekroju dużego wału (świeżo usypanego).
Ten wał jest tak naprawdę graniastosłupem o podstawie trapezowej (można go sobie obrócić by sobie to lepiej wyobrazić). Spróbujmy więc na początku obliczyć pole powierzchni tego trapezu, które będzie jednocześnie polem podstawy graniastosłupa. Przed chwilą wyliczyliśmy sobie, że jego wysokość będzie równa \(15m\), natomiast długości podstawy dolnej i górnej się nie zmienią (bo tak wynika z treści zadania). W związku z tym pole trapezu wyniesie:
$$P_{p}=\frac{1}{2}(a+b)\cdot H \\
P_{p}=\frac{1}{2}\cdot(16m+6m)\cdot15m \\
P_{p}=\frac{1}{2}\cdot22m\cdot15m \\
P_{p}=11m\cdot15m \\
P_{p}=165m^2$$
Krok 3. Obliczenie objętości wału.
Z racji tego iż wał ma długość \(100m\), to jego objętość będzie równa:
$$V=P_{p}\cdot H \\
V=165m^2\cdot100m \\
V=16500m^3$$
To oznacza, że do usypania wału potrzebujemy \(16500m^3\) ziemi.
Zadanie 14. (4pkt) Przekrój poprzeczny ziemnego wału przeciwpowodziowego ma mieć kształt równoramiennego trapezu o podstawach długości \(6m\) i \(16m\) oraz wysokości \(12m\). Trzeba jednak usypać wyższy wał, bo przez dwa lata ziemia osiądzie i wysokość wału zmniejszy się o \(20\%\) (szerokość wału u podnóża i na szczycie nie zmienia się).

Po zakończeniu osiadania ziemi, w celu zmniejszenia przesiąkania, na zboczu wału od strony wody zostanie ułożona warstwa gliny. Oblicz pole powierzchni, którą trzeba będzie wyłożyć gliną na \(100\)-metrowym odcinku tego wału (wał ma kształt graniastosłupa prostego). Wynik podaj z jednostką.
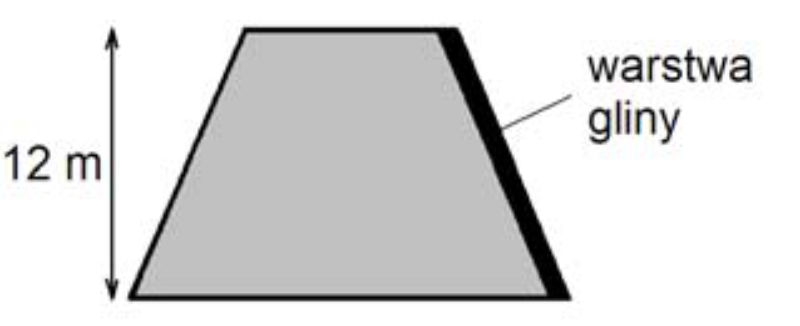
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy podzielisz dolną podstawę na odcinki o długościach \(5m, 6m, 5m\) (Krok 1.).
2 pkt
• Gdy obliczysz długość ramienia trapezu (Krok 2.).
3 pkt
• Gdy obliczysz pole powierzchni prostokąta będącego zboczem wału (Krok 3.), ale otrzymany wynik jest niepoprawny z powodu błędu rachunkowego.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.

Z racji tego iż jest to trapez równoramienny to możemy skorzystać z jego własności i w ten sposób podzielić \(16m\) długości dolnej podstawy na odcinki o długościach \(5m, 6m, 5m\) (tak jak zaznaczono na rysunku).
Krok 2. Obliczenie długości ramienia trapezu.
Musimy obliczyć długość odcinka \(x\), który przyda nam się do obliczenia pola powierzchni warstwy gliny. Skorzystamy tutaj z Twierdzenia Pitagorasa i trójkąta prostokątnego o bokach \(5m\), \(12m\) oraz \(x\):
$$5^2+12^2=x^2 \\
25+144=x^2 \\
x^2=169 \\
x=13[m]$$
Krok 3. Obliczenie pola powierzchni prostokąta.
Powierzchnia zbocza wału jest prostokątem o bokach \(13m\) oraz \(100m\). To oznacza, że poszukiwane pole będzie równe:
$$P=13m\cdot100m=1300m^2$$