Matura próbna z matematyki (poziom podstawowy) - Operon 2012
Arkusz maturalny zawiera 23 zadania zamknięte oraz 9 zadań otwartych. Łącznie do zdobycia jest 50 punktów, a sugerowany maksymalny czas rozwiązywania to 170 minut.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Wartość liczby \(a=16\sqrt[3]{4}\) jest równa wartości liczby:
Zadanie 2. (1pkt) Miejscem zerowym funkcji \(f\) określonej wzorem \(f(x)=\begin{cases} x^2-1\quad \text{ dla } x\in (-\infty,-4 \rangle\\ 5x+10\quad \text{ dla } x\in (-4 ,2)\\ x+4\quad \text{ dla } x\in \langle 2,+\infty) \end{cases}\) jest:
Zadanie 3. (1pkt) Funkcja \(f\), określona wzorem \(f(x)=x^2-3x-4\), przyjmuje wartości ujemne jedynie w przedziale:
Zadanie 4. (1pkt) Wartość liczby \(25^{\log_{5}2}\) jest równa:
Zadanie 5. (1pkt) Dany jest ciąg \((a_{n})\) o wyrazie ogólnym \(a_{n}=-n^2+16\) dla \(n\ge1\). Liczba dodatnich wyrazów tego ciągu jest równa:
Zadanie 6. (1pkt) Kwotę \(10000\) zł wpłacamy do banku na \(4\) lata. Kapitalizacja odsetek jest dokonywana w tym banku co kwartał, a roczna stopa procentowa wynosi \(3\%\). Po \(4\) latach kwotę na rachunku będzie można opisać wzorem:
Zadanie 7. (1pkt) Dane liczby: \(x=\frac{3}{\sqrt{5}-2},\ y=\frac{12}{\sqrt{5}-1}+1,\ z=3\sqrt{5}+2\) tworzą rosnący ciąg arytmetyczny w kolejności:
Zadanie 8. (1pkt) Suma \(2n\) początkowych liczb naturalnych dodatnich parzystych jest równa:
Zadanie 9. (1pkt) W trójkącie równoramiennym wysokość jest dwa razy dłuższa od podstawy. Wynika stąd, że sinus kąta przy podstawie wynosi:
Zadanie 10. (1pkt) Dziedziną funkcji \(f\), określonej wzorem \(f(x)=\frac{x-5}{x^2+4}\), jest zbiór:
Zadanie 11. (1pkt) Liczbą przeciwną do liczby \(a=5^{\frac{2}{3}}\) jest:
Zadanie 12. (1pkt) Wzór funkcji, której wykres powstaje przez przesunięcie wykresu funkcji \(f\) o \(10\) jednostek w dół, to:
Zadanie 13. (1pkt) Rzucono sześcienną kostką do gry. Prawdopodobieństwo, że wyrzucona liczba oczek jest liczbą pierwszą, wynosi:
Zadanie 14. (1pkt) Kąt \(α\) jest ostry i \(tgα=\frac{12}{5}\). Wówczas \(\cosα\) jest równy:
Zadanie 15. (1pkt) Wielomian \(W(x)=x^3-2x^2-4x+8\) po rozłożeniu na czynniki ma postać wyrażenia:
Zadanie 16. (1pkt) Zbiór \((-\infty,-8\rangle\cup\langle-4,+\infty)\) jest rozwiązaniem nierówności:
Zadanie 17. (1pkt) Funkcja \(f(x)=2x^2-4x+5\) jest malejąca w przedziale:
Zadanie 18. (1pkt) Proste \(l\) i \(k\) są prostopadłe i \(l{:}\ 2x-9y+6=0,\ k{:}\ y=ax+b\). Wówczas:
Zadanie 19. (1pkt) Iloraz ciągu geometrycznego o wyrazie ogólnym \(a_{n}=2\cdot7^n\) jest równy:
Zadanie 20. (1pkt) Równanie \((x+6)^2+y^2=4\) opisuje okrąg o środku w punkcie \(S\) i promieniu \(r\). Wówczas:
Zadanie 21. (1pkt) Długość promienia \(r\) okręgu opisanego na kwadracie jest równa \(2\sqrt{3}\). Długość boku tego kwadratu ma wartość:
Zadanie 22. (1pkt) W turnieju szachowym, rozgrywanym systemem każdy z każdym, bez rewanżu, miało brać udział \(8\) zawodników. Jeden z nich zrezygnował. Liczba zaplanowanych rozgrywek zmniejszyła się o:
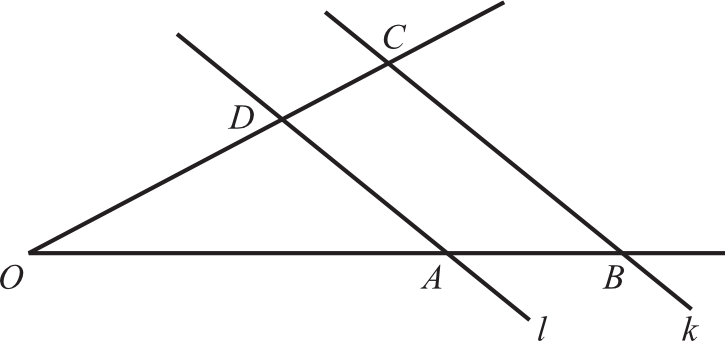
Zadanie 23. (1pkt) Proste \(l\) i \(k\) są równoległe oraz \(|OA|=6, |AB|=10, |OC|=48\). Odcinek \(OD\) ma długość:
Zadanie 24. (2pkt) W ciągu arytmetycznym \((a_{n})\) drugi wyraz jest równy \(7\), a szósty \(17\). Wyznacz pierwszy wyraz i różnicę tego ciągu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz poprawny układ równań (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Utworzenie układu równań.
Korzystając ze wzoru na \(n\)-ty wyraz ciągu arytmetycznego \(a_{n}=a_{1}+(n-1)r\) możemy zapisać, że:
$$\begin{cases}
a_{2}=a_{1}+r \\
a_{6}=a_{1}+5r
\end{cases}$$
$$\begin{cases}
7=a_{1}+r \\
17=a_{1}+5r
\end{cases}$$
Krok 2. Wyznaczenie różnicy ciągu arytmetycznego.
Musimy rozwiązać nasz układ równań. Możemy to zrobić metodą podstawiania (wyznaczając \(a_{1}\) z jednego równania i podstawiając to do drugiego równania), albo też możemy po prostu odjąć te równania stronami otrzymując:
$$-10=-4r \\
r=2\frac{1}{2}$$
Krok 3. Obliczenie wartości pierwszego wyrazu.
Znając różnicę ciągu możemy teraz skorzystać z jednego z równań znajdujących się w układzie i możemy wyliczyć tym samym wartość pierwszego wyrazu:
$$a_{2}=a_{1}+r \\
7=a_{1}+2\frac{1}{2} \\
a_{1}=4\frac{1}{2}$$
Zadanie 25. (2pkt) Średni wzrost sportowców w drużynie siatkarskiej, liczącej \(6\) chłopców, wynosił \(174\) cm. Po przyjęciu do zespołu dwóch braci o tej samej wysokości średnia wzrostu zwiększyła się o \(0,5\) cm. Oblicz, jak wysocy są bracia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz łączny wzrost drużyny przed przyjęciem braci (patrz: Krok 1.).
ALBO
• Gdy ułożysz równanie typu \(\frac{6\cdot174+2x}{8}=174,5\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie sumy wzrostu drużyny przed przyjęciem braci.
Skoro było \(6\) chłopców, a każdy z nich miał średnio \(174cm\), to łącznie wszyscy mieli:
$$6\cdot174cm=1044cm$$
Krok 2. Obliczenie sumy wzrostu drużyny po przyjęciu braci.
Po przyjęciu braci drużyna liczby \(8\) osób i jej średnia wzrostu wynosi \(174,5cm\). W związku z tym wszyscy łącznie mają:
$$8\cdot174,5cm=1396cm$$
Krok 3. Obliczenie wzrostu braci.
Razem bracia mają:
$$1396cm-1044cm=352cm$$
Skoro bracia są tego samego wzrostu, to każdy z nich ma:
$$352cm:2=176cm$$
Zadanie 26. (2pkt) Rozwiąż równanie \(2x^3+8x^2-3x-12=0\)
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy pogrupujesz wyrazy i wyłączysz odpowiednie czynniki przed nawias w taki sposób, że w nawiasach jest jednakowa wartość, dzięki której można szybko przejść do postaci iloczynowej albo wręcz doprowadzisz równanie do postaci iloczynowej (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wyłączenie odpowiednich czynników przed nawias i zapisanie równania w postaci iloczynowej.
W tego typu zadaniach musimy wyłączyć wspólne części przed nawias. Wspólną częścią pierwszego i drugiego wyrazu jest \(2x^2\), a z trzeciego i czwartego wyrazu możemy wyłączyć liczbę \(-3\). To oznacza, że:
$$2x^3+8x^2-3x-12=0 \\
2x^2(x+4)-3(x+4)=0 \\
(2x^2-3)(x+4)=0$$
Krok 2. Wyznaczenie rozwiązań z postaci iloczynowej.
Korzystając z postaci iloczynowej możemy teraz przyrównać wartości w nawiasach do zera, wyznaczając w ten sposób rozwiązania naszej równości.
$$2x^2-3=0 \quad\lor\quad x+4=0$$
Pierwsze równanie jest równaniem kwadratowym, które możemy obliczyć tradycyjnie deltą, ale możemy też to rozpisać w następujący sposób:
$$2x^2-3=0 \\
2x^2=3 \\
x^2=\frac{3}{2} \\
x=\sqrt{\frac{3}{2}} \quad\lor\quad x=-\sqrt{\frac{3}{2}}$$
Z drugiego równania otrzymamy:
$$x+4=0 \\
x=-4$$
To oznacza, że nasze równanie z treści zadania ma łącznie trzy rozwiązania:
$$x=\sqrt{\frac{3}{2}} \quad\lor\quad x=-\sqrt{\frac{3}{2}} \quad\lor\quad x=-4$$
Zadanie 27. (2pkt) Rozwiąż nierówność \(x^2-9\gt0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz miejsca zerowe, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe funkcji (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).
Wyjaśnienie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Aby rozwiązać nierówność musimy najpierw sprawdzić jakie ma miejsca zerowe, czyli musimy sprawdzić dla jakich argumentów \(x^2-9=0\). Możemy to zrobić tradycyjnie (tak jak to zazwyczaj bywa) metodą delty, ale akurat w tym przypadku jesteśmy w stanie to powstałe równanie kwadratowe obliczyć w pamięci, bo:
$$x^2-9=0 \\
x^2=9 \\
x=3 \quad\lor\quad x=-3$$
Krok 2. Szkicowanie wykresu paraboli.
Zaznaczamy na osi obliczone miejsca zerowe i rysujemy przechodzącą przez te punkty parabolę z ramionami skierowanymi do góry (bo przed \(x^2\) nie stoi żadna ujemna wartość):

Krok 3. Odczytanie rozwiązania.
Interesują nas argumenty, dla których nierówność przyjmuje wartości większe od zera. W związku z tym rozwiązaniem tej nierówności jest suma przedziałów:
$$x\in(-\infty;-3)\cup(3;+\infty)$$
Zadanie 28. (2pkt) Dana jest liczba \(a=\sqrt{(2-2\sqrt{5})^2}-2\sqrt{5}\). Wykaż, że liczba \(a\) jest całkowita.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie pozbędziesz się pierwiastka (patrz: Krok 1.).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Obliczenie wartości pierwiastka.
Zadanie jest dość podchwytliwe, a kluczem do sukcesu jest poprawne pozbycie się pierwiastka. Zastanówmy się jaka wartość wyjdzie nam z pierwiastkowania liczby \(\sqrt{(2-2\sqrt{5})^2}\). Czy będzie to po prostu \(2-2\sqrt{5}\)? Gdyby tak było, to mielibyśmy sytuację w której z pierwiastka kwadratowego wyjdzie nam wynik ujemny (bo \(2-2\sqrt{5}\) jest ujemne), a to jest przecież sprzeczne z definicją pierwiastka. Czy to oznacza, że zadanie ma błąd? Wszystko jest w porządku, ponieważ wartość \(2-2\sqrt{5}\) jest faktycznie ujemna, jednak podniesiona do kwadratu daje już liczbę dodatnią, no a pierwiastkowanie liczby dodatniej daje liczbę dodatnią.
Musimy po prostu pamiętać, że \(\sqrt{x^2}=|x|\). Teraz sprawa jest już jasna i to oznacza, że \(\sqrt{(2-2\sqrt{5})^2}=|2-2\sqrt{5}|\).
Krok 2. Pozbycie się wartości bezwzględnej.
To jednak nie koniec zadania. Aby wykonać dalsze odejmowanie, które znajduje się na końcu przykładu musimy pozbyć się wartości bezwzględnej. Ustaliliśmy już, że \(2-2\sqrt{5}\) jest liczbą ujemną. Jeżeli mamy przykładowo obliczyć wartość bezwzględną z liczby ujemnej, np. \(|-5|\) to opuszczając wartość bezwzględną zmieniamy znak i dlatego np. \(|-5|=5\). W naszym przypadku to oznacza, że:
$$|2-2\sqrt{5}|=-(2-2\sqrt{5})=-2+2\sqrt{5}$$
Krok 3. Obliczenie wartości wyrażenia i zakończenie dowodzenia.
Wiemy już, że z pierwiastka wyjdzie nam wynik \(-2+2\sqrt{5}\) i od tej liczby zgodnie z wyrażeniem musimy jeszcze odjać \(2\sqrt{5}\), otrzymując:
$$a=-2+2\sqrt{5}-2\sqrt{5} \\
a=-2$$
\(-2\) jest liczbą całkowitą, zatem dowodzenie możemy uznać za zakończone.
Zadanie 29. (2pkt) Długość krawędzi sześcianu zwiększono o \(20\%\). Oblicz, o ile procent wzrosła objętość tego sześcianu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie zapiszesz długość krawędzi sześcianu przed powiększeniem i po powiększeniu.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
\(a\) - długość krawędzi sześcianu przed powiększeniem
\(1,2a\) - długość krawędzi sześcianu po powiększeniu
\(V=a^3\) - objętość sześcianu przed powiększeniem
\(V=1,2a\cdot1,2a\cdot1,2a=1,728a^3\) - objętość sześcianu po powiększeniu
Skoro przed powiększeniem sześcian miał objętość \(a^3\) (czyli \(1a^3\)), a po powiększeniu ma objętość równą \(1,728a^3\) to objętość wzrosła o \(72,8\%\).
Zadanie 30. (5pkt) Prosta \(y=x+4\) przecina okrąg o równaniu \((x+1)^2+(y-2)^2=25\) w punktach \(A\) i \(B\). Oblicz współrzędne punktów \(A\) i \(B\), a następnie oblicz obwód trójkąta \(ABS\), gdzie \(S\) jest środkiem danego okręgu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie zapiszesz równanie z jedną niewiadomą np. \((x+1)^2+(x+4-2)^2=25\) (patrz: Krok 1.).
2 pkt
• Gdy obliczysz błędnie współrzędne punktu \(A\) lub \(B\), bo popełnisz błąd rachunkowy np. przy wyliczaniu delty (patrz: Krok 3.).
3 pkt
• Gdy obliczysz współrzędne punktów \(A\) oraz \(B\) (patrz: Krok 3.).
4 pkt
• Gdy obliczysz długość odcinka \(AB\) (patrz: Krok 6.).
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Ułożenie i rozwiązanie układu równań.
Ze wzoru prostej oraz równania okręgu możemy ułożyć następujący układ równań:
$$\begin{cases}
y=x+4 \\
(x+1)^2+(y-2)^2=25
\end{cases}$$
Podstawiając pierwsze równanie do drugiego otrzymamy:
$$(x+1)^2+(x+4-2)^2=25 \\
(x+1)^2+(x+2)^2=25 \\
x^2+2x+1+x^2+4x+4=25 \\
2x^2+6x-20=0 \quad\bigg/:2 \\
x^2+3x-10=0$$
Krok 2. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=1,\;b=3,\;c=-10\)
$$Δ=b^2-4ac=3^2-4\cdot1\cdot(-10)=9-(-40)=9+40=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-3-7}{2\cdot1}=\frac{-10}{2}=-5 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-3+7}{2\cdot1}=\frac{4}{2}=2$$
Krok 3. Zapisanie współrzędnych przecięcia się prostej z okręgiem.
Otrzymaliśmy dwie współrzędne iksowe, bo i nasza prosta (zgodnie z treścią zadania) przecina okrąg w dwóch miejscach. To oznacza, że pierwsza współrzędna iksowa należy do punktu \(A\), natomiast druga współrzędna należy do punktu \(B\). Musimy jeszcze obliczyć współrzędne igrekowe, a zrobimy to podstawiając współrzędne iksowe do równania prostej \(y=x+4\):
Dla \(x=-5\):
\(y=-5+4\)
\(y=-1\)
Dla \(x=2\):
\(y=2+4=6\)
To nam daje następujące współrzędne:
$$A=(-5;-1),\;B=(2;6)$$
Krok 4. Obliczenie długości promienia.
Równanie okręgu o środku w punkcie \(S=(a;b)\) oraz promieniu \(r\) przyjmuje postać:
$$(x-a)^2+(y-b)^2=r^2$$
Teraz do tej postaci możemy przyrównać równanie z treści zadania. W naszym równaniu z treści zadania po prawej stronie znalazła się wartość \(25\), zatem jest to nasze \(r^2\). Możemy więc zapisać, że:
$$r^2=25 \\
r=5 \quad\lor\quad r=-5$$
Ujemne rozwiązanie oczywiście odrzucamy, bo promień nie może być ujemny.
Krok 5. Sporządzenie rysunku pomocniczego i zapisanie długości boków \(AS\) oraz \(BS\).
Z równania okręgu możemy wprost odczytać, że współrzędne środka okręgu to \(S=(-1;2)\). Ta informacja w połączeniu z obliczeniami z kroków poprzednich, czyli długość promienia \(r=5\) oraz współrzędne punktów \(A=(-5;-1),\;B=(2;6)\) pozwoli nam stworzyć następujący rysunek pomocniczy:
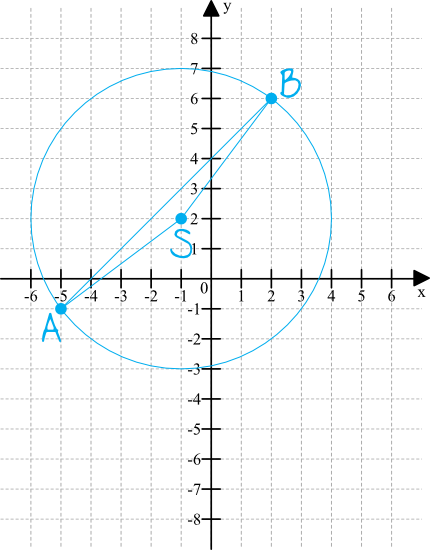
Z rysunku dość jasno wynika, że odcinki o długości \(AS\) oraz \(AB\) są równe długości promienia, zatem możemy zapisać, że:
$$|AS|=5 \\
|BS|=5$$
Krok 6. Obliczenie długości odcinka \(AB\).
Skorzystamy ze wzoru na długość odcinka w układzie współrzędnych, ponieważ znamy współrzędne punktów \(A\) oraz \(B\).
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2} \\
|AB|=\sqrt{(2-(-5))^2+(6-(-1))^2} \\
|AB|=\sqrt{7^2+7^2} \\
|AB|=\sqrt{49+49} \\
|AB|=\sqrt{49\cdot2} \\
|AB|=7\sqrt{2}$$
Krok 7. Obliczenie długości obwodu.
Mamy już wszystkie niezbędne informacje, zatem możemy bez problemu obliczyć długość obwodu:
$$Obw=5+5+7\sqrt{2}=10+7\sqrt{2}$$
Zadanie 31. (5pkt) Dany jest ostrosłup prawidłowy trójkątny. Pole powierzchni bocznej tego ostrosłupa jest równe \(24\), a kąt płaski ściany bocznej przy podstawie ma miarę \(α\) i \(tgα=2\). Wyznacz cosinus kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy sporządzisz rysunek pomocniczy i wprowadzisz poprawne oznaczenia (patrz: Krok 1.).
2 pkt
• Gdy zapiszesz równania (lub układ równań) wynikające z tangensa i pola powierzchni bocznej (patrz: Krok 2. oraz 3.), ale ich nie rozwiążesz i na tym zakończysz zadanie.
3 pkt
• Gdy obliczysz długość krawędzi podstawy i wysokości ściany bocznej (patrz: Krok 3.).
4 pkt
• Gdy doprowadzisz zadanie do samego końca, ale otrzymany wynik będzie zły jedynie ze względu na błąd rachunkowy.
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Na początku stwórzmy prosty rysunek pomocniczy, na którym zaznaczymy przede wszystkim kąt \(α\) (co stanowi w sumie jedną z większych pułapek tego zadania, bo zazwyczaj zaznaczamy inne kąty w ostrosłupie niż kąt płaski ściany bocznej) oraz kąt \(β\), który jest kątem nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawy:
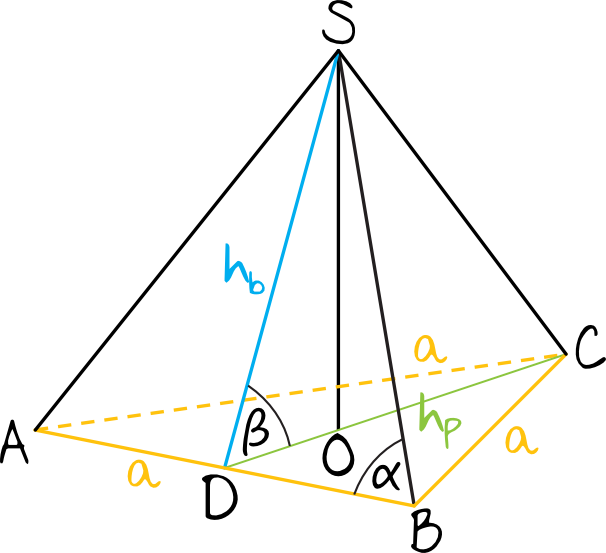
Krok 2. Rozpisanie tangensa.
Spójrzmy na trójkąt prostokątny \(DBS\), który utworzył nam się na rysunku pomocniczym. Wiemy, że tangens to stosunek długości przyprostokątnej leżącej naprzeciw kąta \(α\) do długości przyprostokątnej leżącej przy tym kącie. W naszym przypadku otrzymamy więc następujące równanie:
$$tgα=\frac{h_{b}}{\frac{1}{2}a} \\
2=\frac{h_{b}}{\frac{1}{2}a} \quad\bigg/\cdot\frac{1}{2}a \\
a=h_{b}$$
Z naszych obliczeń wynika więc, że wysokość ściany bocznej jest równa długości krawędzi podstawy.
Krok 3. Obliczenie długości krawędzi podstawy.
Skorzystamy teraz z informacji, która mówi że pole powierzchni bocznej tego ostrosłupa jest równe \(24\). W naszym ostrosłupie mamy \(3\) identyczne ściany boczne, zatem pole powierzchni każdej z nich jest równe:
$$P_{b}=24:3=8$$
W ścianie bocznej znajduje się trójkąt o podstawie \(a\) oraz wysokości \(h_{b}\), która jak już ustaliliśmy jest równa długości \(a\), zatem:
$$P=\frac{1}{2}a\cdot h_{b} \\
8=\frac{1}{2}a\cdot a \\
16=a^2 \\
a=4 \quad\lor\quad a=-4$$
Wartość ujemną oczywiście odrzucamy, bo długość nie może być ujemna. W związku z tym \(a=4\) i tym samym \(h_{b}=4\).
Krok 4. Obliczenie wysokości trójkąta znajdującego się w podstawie oraz obliczenie długości odcinka \(AO\).
Spójrzmy teraz na trójkąt prostokątny \(AOS\) z zaznaczonym kątem \(β\). To właśnie cosinus tego kąta musimy wyznaczyć, a do tego niezbędna będzie znajomość odcinka \(AO\). Czym jest ten odcinek \(AO\)? Jest to długość \(\frac{1}{3}\) wysokości trójkąta równobocznego znajdującego się w podstawie (wynika to z własności trójkątów równobocznych). Musimy więc obliczyć wysokość trójkąta równobocznego, korzystając z następującego wzoru:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
h_{p}=\frac{4\sqrt{3}}{2} \\
h_{p}=2\sqrt{3}$$
Odcinek \(AO\) jest zatem równy:
$$|AO|=\frac{1}{3}\cdot2\sqrt{3}=\frac{2\sqrt{3}}{3}$$
Krok 5. Obliczenie wartości cosinusa.
Mamy już komplet informacji do obliczenia cosinusa, bowiem cosinus opisuje zależność między przyprostokątną leżącą przy kącie (u nas jest to \(|AO|=\frac{2\sqrt{3}}{3}\), a przeciwprostokątną (u nas jest to \(h_{b}=4\)). W związku z tym:
$$cosβ=\frac{\frac{2\sqrt{3}}{3}}{4} \\
cosβ=\frac{2\sqrt{3}}{3}\cdot\frac{1}{4} \\
cosβ=\frac{\sqrt{3}}{6}$$
Zadanie 32. (5pkt) Turysta pokonał pieszo trasę długości \(30km\) z miejscowości \(A\) do miejscowości \(B\) ze stałą prędkością. Rowerem poruszałby się z prędkością o \(9\frac{km}{h}\) większą i przybyłby do celu o \(3\) godziny wcześniej. Wyznacz prędkość marszu turysty i czas przejścia tej drogi.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wprowadzisz poprawne oznaczenia (patrz: Krok 1.).
2 pkt
• Gdy zapiszesz poprawny układ równań (patrz: Krok 2.).
3 pkt
• Gdy doprowadzisz do postaci ogólnej równania kwadratowego z którego potem można obliczyć deltę (patrz: Krok 2.).
4 pkt
• Gdy doprowadzisz zadanie do samego końca, ale otrzymany wynik będzie zły jedynie ze względu na błąd rachunkowy.
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wprowadzenie oznaczeń do zadania.
\(s=30\) - pokonana trasa (w \(km\))
\(v_{1}\) - prędkość marszu (w \(\frac{km}{h}\))
\(v_{2}=v_{1}+9\) - prędkość jazdy rowerem (w \(\frac{km}{h}\))
\(t_{1}\) - czas marszu (w godzinach)
\(t_{2}=t_{1}-3\) - czas jazdy rowerem (w godzinach)
Krok 2. Utworzenie i rozwiązanie układu równań.
Skorzystamy teraz ze wzoru na drogę \(s=vt\) i zapiszemy w formie układu równań, relację dotyczącą prędkości marszu oraz jazdy rowerem:
$$\begin{cases}
s=v_{1}\cdot t_{1} \\
s=v_{2}\cdot t_{2}
\end{cases}$$
$$\begin{cases}
30=v_{1}\cdot t_{1} \\
30=v_{2}\cdot t_{2}
\end{cases}$$
Podstawiając pod drugie równanie dane z kroku pierwszego otrzymamy:
$$\begin{cases}
30=v_{1}\cdot t_{1} \\
30=(v_{1}+9)\cdot (t_{1}-3)
\end{cases}$$
$$\begin{cases}
v_{1}=\frac{t_{1}}{180} \\
180=(v_{1}+9)\cdot (t_{1}-3)
\end{cases}$$
Teraz skorzystamy z metody podstawiania i podstawimy \(v_{1}\) z pierwszego równania do drugiego:
$$30=\left(\frac{t_{1}}{30}+9\right)\cdot(t_{1}-3)$$
Wymnażając poszczególne nawiasy i upraszczając zapis do postaci ogólnej otrzymamy:
$$30=30-\frac{90}{t_{1}}+9t_{1}-27 \quad\bigg/-30 \\
-\frac{90}{t_{1}}+9t_{1}-27=0 \quad\bigg/\cdot t_{1} \\
-90+9t_{1}^2-27t_{1}=0 \quad\bigg/:9 \\
-10+t_{1}^2-3t_{1}=0 \\
t_{1}^2-3t_{1}-10=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=1,\;b=-3,\;c=-10\)
$$Δ=b^2-4ac=(-3)^2-4\cdot1\cdot(-10)=9-(-40)=9+40=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$t_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-3)-7}{2\cdot1}=\frac{3-7}{2}=\frac{-4}{2}=-2 \\
t_{1}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-3)+7}{2\cdot1}=\frac{3+7}{2}=\frac{10}{2}=5$$
Ujemny wynik musimy odrzucić, bowiem czas nie może być ujemny. To oznacza, że \(t_{1}=5\).
Krok 4. Obliczenie prędkości marszu.
Znamy długość drogi \(s=30km\), wiemy też że czas jazdy wynosi \(t=5h\), zatem bez problemu obliczymy prędkość marszu:
$$v=\frac{s}{t} \\
v=\frac{30km}{5h} \\
v=6\frac{km}{h}$$