Matura poprawkowa z matematyki (poziom podstawowy) - Sierpień 2019
Arkusz maturalny zawiera 25 zadań zamkniętych oraz 9 zadań otwartych. Łącznie do zdobycia jest 50 punktów, a sugerowany maksymalny czas rozwiązywania to 170 minut.
Zadanie 1. (1pkt) Liczba \(log_{\sqrt{7}}7\) jest równa:
Zadanie 2. (1pkt) Kwadrat liczby \(8-3\sqrt{7}\) jest równy:
Zadanie 3. (1pkt) Jeżeli \(75\%\) liczby \(a\) jest równe \(177\) i \(59\%\) liczby \(b\) jest równe \(177\), to:
Zadanie 4. (1pkt) Równanie \(x(5x+1)=5x+1\) ma dokładnie:
Zadanie 5. (1pkt) Para liczb \(x=3\) i \(y=1\) jest rozwiązaniem układu równań \(\begin{cases} -x+12y=a^2 \\ 2x+ay=9 \end{cases}\) dla:
Zadanie 6. (1pkt) Równanie \(\frac{(x-2)(x+4)}{(x-4)^2}=0\) ma dokładnie:
Zadanie 7. (1pkt) Miejscami zerowymi funkcji kwadratowej \(f\) określonej wzorem \(f(x)=9-(3-x)^2\) są liczby:
Zadanie 8. (1pkt) Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej \(g\). Wierzchołkiem tej paraboli jest punkt \(W=(1;1)\).

Zbiorem wartości funkcji \(g\) jest przedział:
Zadanie 9. (1pkt) Liczbą większą od \(5\) jest:
Zadanie 10. (1pkt) Punkt \(A=(a,3)\) leży na prostej określonej równaniem \(y=\frac{3}{4}x+6\). Stąd wynika, że:
Zadanie 11. (1pkt) W ciągu arytmetycznym \((a_{n})\), określonym dla \(n\ge1\), dane są wyrazy: \(a_{1}=-11\) i \(a_{9}=5\). Suma dziewięciu początkowych wyrazów tego ciągu jest równa:
Zadanie 12. (1pkt) Wszystkie wyrazy ciągu geometrycznego \((a_{n})\), określonego dla \(n\ge1\), są liczbami dodatnimi. Drugi wyraz tego ciągu jest równy \(162\), a piąty wyraz jest równy \(48\). Oznacza to, że iloraz tego ciągu jest równy:
Zadanie 13. (1pkt) Cosinus kąta ostrego \(α\) jest równy \(\frac{12}{13}\). Wtedy:
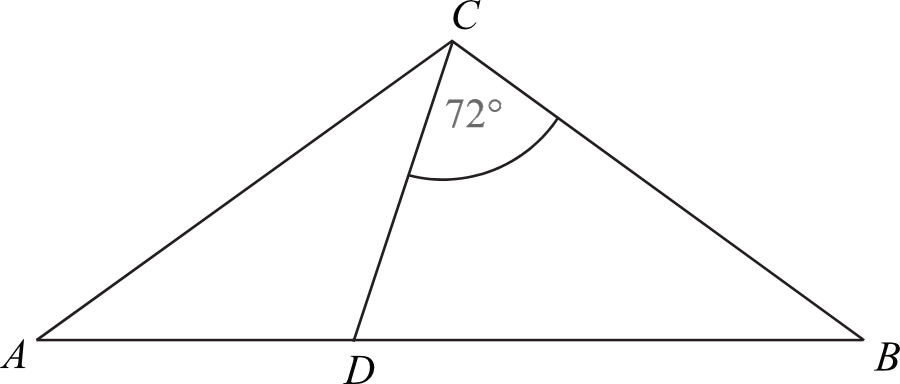
Zadanie 14. (1pkt) Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Na podstawie \(AB\) tego trójkąta leży punkt \(D\), taki że \(|AD|=|CD|\), \(|BC|=|BD|\) oraz \(\sphericalangle BCD=72°\) (zobacz rysunek). Wynika stąd, że kąt \(ACD\) ma miarę:
Zadanie 15. (1pkt) Okrąg, którego środkiem jest punkt \(S=(a;5)\), jest styczny do osi \(Oy\) i do prostej o równaniu \(y=2\). Promień tego okręgu jest równy:
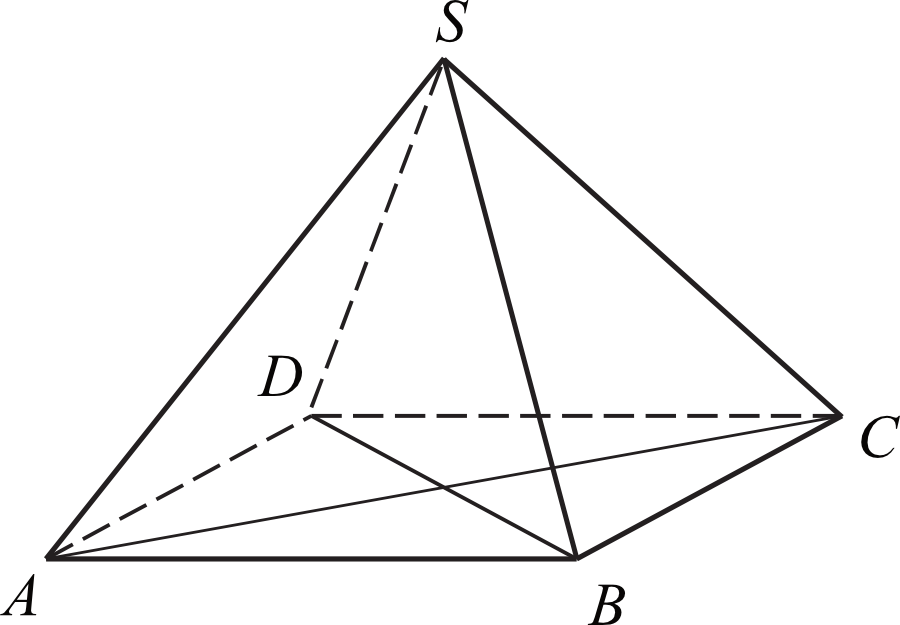
Zadanie 16. (1pkt) Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\) (zobacz rysunek). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta \(SAC\) jest równa:
Zadanie 17. (1pkt) Proste o równaniach \(y=(4m+1)x-19\) oraz \(y=(5m-4)x+20\) są równoległe, gdy:
Zadanie 18. (1pkt) W układzie współrzędnych punkt \(S=(40; 40)\) jest środkiem odcinka \(KL\), którego jednym z końców jest punkt \(K=(0; 8)\). Zatem:
Zadanie 19. (1pkt) Punkt \(P=(-6,-8)\), przekształcono najpierw w symetrii względem osi \(Ox\), a potem w symetrii względem osi \(Oy\). W wyniku tych przekształceń otrzymano punkt \(Q\). Zatem:
Zadanie 20. (1pkt) W układzie współrzędnych na płaszczyźnie danych jest \(5\) punktów: \(A=(1,4)\), \(B=(-5,-1)\), \(C=(-5,3)\), \(D=(6,-4)\), \(P=(-30,-76)\). Punkt \(P\) należy do tej samej ćwiartki układu współrzędnych co punkt:
Zadanie 21. (1pkt) Dany jest prostopadłościan o wymiarach \(30cm\times40cm\times120cm\) (zobacz rysunek), a ponadto dane są cztery odcinki \(a,b,c,d\), o długościach - odpowiednio - \(119cm\), \(121cm\), \(129cm\) i \(131cm\).
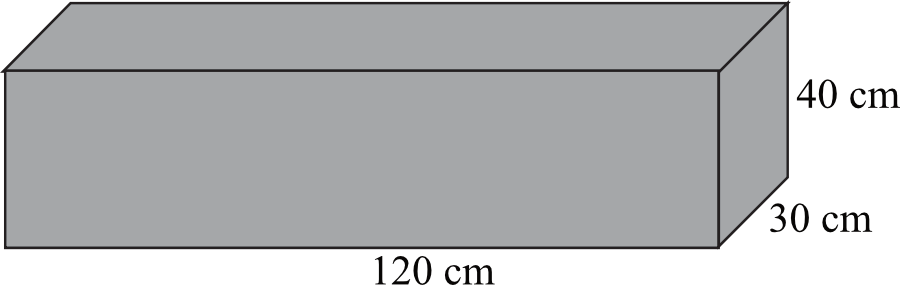
Przekątna tego prostopadłościanu jest dłuższa:
Zadanie 22. (1pkt) Pole powierzchni całkowitej pewnego stożka jest \(3\) razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy \(2\) i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą:
Zadanie 23. (1pkt) Średnia arytmetyczna dziesięciu liczb naturalnych \(3,10,5,x,x,x,x,12,19,7\) jest równa \(12\). Mediana tych liczb jest równa:
Zadanie 24. (1pkt) Wszystkich liczb naturalnych czterocyfrowych parzystych, w których występują wyłącznie cyfry \(1,2,3\) jest:
Zadanie 25. (1pkt) W grupie \(60\) osób (kobiet i mężczyzn) jest \(35\) kobiet. Z tej grupy losujemy jedną osobę. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwa zdarzenia polegającego na tym, że wylosujemy mężczyznę, jest równe:
Zadanie 26. (2pkt) Rozwiąż równanie \((x^2-16)(x^3-1)=0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz dwa równania \(x^2-16=0\) oraz \(x^3-1=0\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Aby to równanie było równe \(0\), to wartość któregoś z nawiasów musi być równa \(0\). W związku z tym:
$$x^2-16=0 \quad\lor\quad x^3-1=0 \\
x^2=16 \quad\lor\quad x^3=1 \\
x=4\quad\lor\quad x=-4 \quad\lor\quad x=1$$
Zadanie 27. (2pkt) Rozwiąż nierówność \(2x^2-5x+3\le0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz miejsca zerowe, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe funkcji (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).
Wyjaśnienie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Najprościej będzie wyliczyć to tzw. metodą delty.
Współczynniki: \(a=2,\;b=-5,\;c=3\)
$$Δ=b^2-4ac=(-5)^2-4\cdot2\cdot3=25-24=1 \\
\sqrt{Δ}=\sqrt{1}=1$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-5)-1}{2\cdot2}=\frac{5-1}{4}=\frac{4}{4}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-5)+1}{2\cdot2}=\frac{5+1}{4}=\frac{6}{4}=\frac{3}{2}$$
Krok 2. Szkicowanie wykresu paraboli.
Współczynnik \(a\) jest dodatni, zatem ramiona paraboli będą skierowane do góry. Zaznaczamy na osi miejsca zerowe obliczone przed chwilą i szkicujemy wykres paraboli:

Miejsca zerowe \(x=1\) oraz \(x=\frac{3}{2}\) mają zamalowane kropki, bo w nierówności wystąpił znak \(\le\).
Krok 3. Odczytanie rozwiązania.
Z wykresu możemy odczytać, że funkcja przyjmuje wartości mniejsze od zera dla przedziału \(x\in\langle1;\frac{3}{2}\rangle\) i taka też jest nasza ostateczna odpowiedź.
Zadanie 28. (2pkt) Wykaż, że dla każdej liczby dodatniej \(x\) prawdziwa jest nierówność \(x+\frac{1-x}{x}\ge1\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie rozpiszesz lewą stronę nierówności otrzymując postać typu \(x^2-2x+1\) (patrz: Krok 1.) lub jakiejkolwiek inną podobną.
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Przekształcenie nierówności.
Pierwszą rzeczą jaką chcielibyśmy zrobić to pomnożyć obydwie strony tego równania przez \(x\). Musimy się jednak pochylić nad tym działaniem, bowiem kiedy mnożymy (lub dzielimy) nierówność przez liczbę ujemną to trzeba zmienić znak nierówności. Tutaj akurat tego problemu nie mamy, bo w treści zadania podano, że dowodzenie ma dotyczyć tylko liczb dodatnich. W związku z tym bez obaw możemy obustronnie pomnożyć to wyrażenie przez \(x\):
$$x+\frac{1-x}{x}\ge1 \quad\bigg/\cdot x \\
x^2+1-x\ge x \\
x^2-2x+1\ge0 \\
(x-1)^2\ge0$$
Krok 2. Interpretacja otrzymanego wyniku.
Każda liczba podniesiona do kwadratu daje nam wynik dodatni lub równy \(0\). Z tego też względu wartość \((x-1)^2\) jest na pewno większa lub równa zero, co kończy nasze dowodzenie.
Zadanie 29. (2pkt) Wierzchołki \(A\) i \(C\) trójkąta \(ABC\) leżą na okręgu o promieniu \(r\), a środek \(S\) tego okręgu leży na boku AB trójkąta (zobacz rysunek). Prosta \(BC\) jest styczna do tego okręgu w punkcie \(C\), a ponadto \(|AC|=r\sqrt{3}\). Wykaż, że kąt \(ACB\) ma miarę \(120°\).
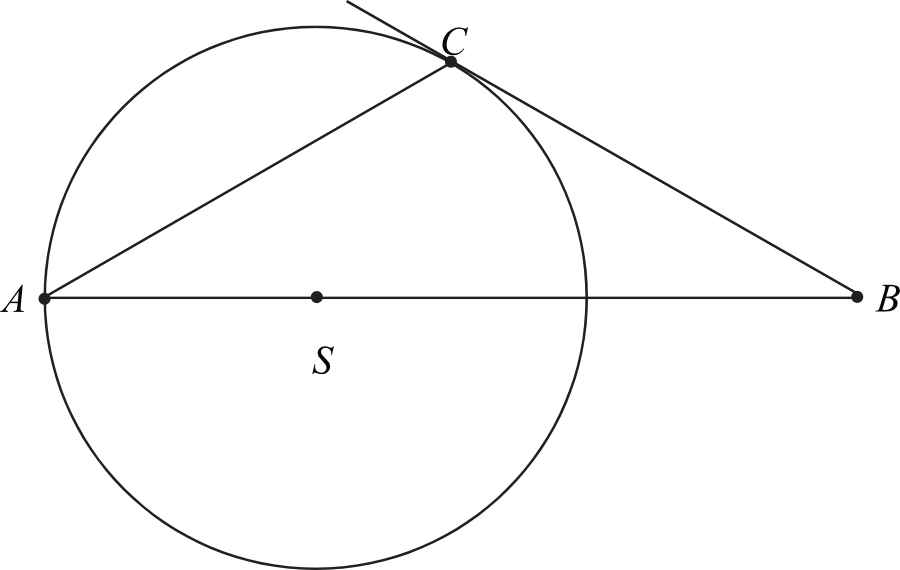
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie obliczysz miarę przynajmniej jednego kąta np. \(ACS\) (patrz: Krok 3.).
ALBO
• Gdy poprawnie obliczysz cosinus jednego z kątów np. \(ACS\) (patrz: Krok 3.).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Kluczem do rozwiązania zadania jest dorysowanie odcinka \(CS\), który jest promieniem okręgu. Z własności stycznych do okręgu wiemy, że styczna tworzy z promieniem kąt prosty i to będzie dla nas bardzo ważna informacja w tym zadaniu dowodowym.
Drugą rzeczą, którą musimy dostrzec to fakt, że dorysowując odcinek \(CS\) utworzy nam się trójkąt równoramienny \(ASC\), którego ramiona są promieniami okręgu, a podstawą jest bok \(AC\). Co więcej, w treści zadania mamy tę długość podstawy opisaną jako \(|AC|=r\sqrt{3}\).
Nanosząc te wszystkie informacje oraz dorysowując jeszcze wysokość trójkąta równoramiennego \(ASC\) otrzymamy następującą sytuację:
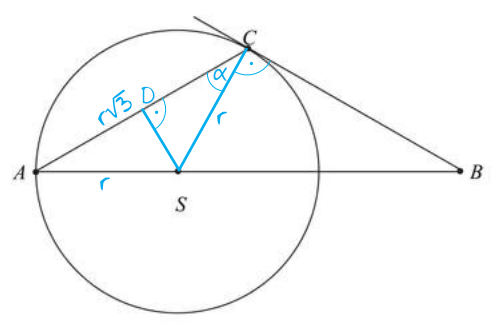
Krok 2. Obliczenie długości odcinka \(DC\).
Spójrzmy na trójkąt prostokątny \(DSC\). Długość odcinka \(DC\) jest równa połowie długości odcinka \(AC\) (bo wysokość padająca na podstawę dzieli podstawę na dwa równe odcinki). Możemy więc zapisać, że:
$$|DC|=\frac{1}{2}\cdot|AC| \\
|DC|=\frac{1}{2}\cdot r\sqrt{3} \\
|DC|=\frac{r\sqrt{3}}{2}$$
Krok 3. Obliczenie miary kąta \(ACS\).
Ponownie spoglądamy na trójkąt prostokątny \(DSC\). Wiemy, że \(|SC|=r\) oraz że \(|DC|=\frac{r\sqrt{3}}{2}\). Korzystając z funkcji trygonometrycznych (a konkretniej z cosinusa) możemy zapisać, że:
$$cosα=\frac{|DC|}{|SC|} \\
cosα=\frac{\frac{r\sqrt{3}}{2}}{r} \\
cosα=\frac{r\sqrt{3}}{2}:r \\
cosα=\frac{r\sqrt{3}}{2}\cdot\frac{1}{r} \\
cosα=\frac{\sqrt{3}}{2}$$
Z tablic trygonometrycznych możemy odczytać, że cosinus przyjmuje taką wartość dla kąta o mierze \(30°\), czyli \(|\sphericalangle ACS|=30°\).
Krok 4. Obliczenie miary kąta \(ACB\) i zakończenie dowodzenia.
Kąt \(ACB\) jest sumą kątów \(ACS\) oraz \(SCB\). Przed chwilą wyliczyliśmy, że \(|\sphericalangle ACS|=30°\), a z własności stycznych do okręgu wiemy, że \(|\sphericalangle SCB|=90°\). W związku z tym:
$$|\sphericalangle ACB|=30°+90°=120°$$
W ten sposób dowodzenie możemy uznać za zakończone.
Zadanie 30. (2pkt) Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru \(\{1,3,5,7,9\}\) i jednocześnie cyfrę jedności, która należy do zbioru \(\{0,2,4,6,8\}\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy wykonasz wszystkie kroki, ale otrzymasz wynik większy od \(1\).
1 pkt
• Gdy obliczysz liczbę wszystkich zdarzeń elementarnych (patrz: Krok 1.).
ALBO
• Gdy obliczysz liczbę wszystkich zdarzeń sprzyjających (patrz: Krok 2.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Ustalenie liczby wszystkich możliwych zdarzeń elementarnych.
Wybieramy jedną liczbę spośród wszystkich liczb naturalnych dwucyfrowych. Skoro naturalnych liczb dwucyfrowych jest \(90\), to znaczy że:
$$|Ω|=90$$
Krok 2. Ustalenie liczby zdarzeń sprzyjających.
Ustalmy najpierw co to jest rząd dziesiątek i jedności. Jeżeli mamy liczbę \(75\), to cyfrą dziesiątek jest \(7\), a cyfrą jedności jest \(5\).
Sprzyjającymi zdarzeniami są liczby, które w rzędzie dziesiątek mają liczbę nieparzystą, a w rzędzie jedności mają liczbę parzystą. Takimi zdarzeniami byłyby więc przykładowo liczby \(14, 38, 52\) itd., ale już przykładowo \(21, 22, 84\) nie są sprzyjające.
Aby ustalić liczbę wszystkich zdarzeń sprzyjających skorzystamy z reguły mnożenia. W rzędzie dziesiątek możemy mieć jedną z pięciu cyfr i w rzędzie jedności także możemy mieć jedną z pięciu cyfr. Zatem zgodnie z regułą mnożenia \(|A|=5\cdot5=25\).
Krok 3. Obliczenie prawdopodobieństwa.
Prawdopodobieństwo obliczymy korzystając ze wzoru:
$$P(A)=\frac{|A|}{|Ω|}=\frac{25}{90}=\frac{5}{18}$$
Zadanie 31. (2pkt) Przekątne rombu \(ABCD\) przecinają się w punkcie \(S=(-\frac{21}{2},-1)\). Punkty \(A\) i \(C\) leżą na prostej o równaniu \(y=\frac{1}{3}x+\frac{5}{2}\). Wyznacz równanie prostej \(BD\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz współczynnik kierunkowy \(a\) prostej \(BD\) (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Ustalenie współczynnika \(a\) prostej \(BD\).
Wiemy, że prosta \(AC\) wyraża się równaniem \(y=\frac{1}{3}x+\frac{5}{2}\), czyli współczynnik kierunkowy \(a\) tej prostej wynosi \(\frac{1}{3}\). Prosta \(BD\) musi być prostopadła do naszej prostej \(AC\), a aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). W związku z tym prosta \(BD\) będzie miała współczynnik \(a\) równy:
$$\frac{1}{3}\cdot a=-1 \\
a=-3$$
Możemy teraz podstawić wyznaczony współczynnik do postaci kierunkowej \(y=ax+b\), a to oznacza, że wzór prostej \(BD\) możemy zapisać już jako \(y=-3x+b\).
Krok 2. Obliczenie współczynnika \(b\) prostej \(BD\).
Do poznania pełnego wzoru brakuje nam jeszcze współczynnika \(b\). Wyznaczymy go podstawiając do otrzymanej przed chwilą postaci \(y=-3x+b\) współrzędne punktu \(S\), przez który ta prosta przechodzi. Podstawiając zatem \(x=-\frac{21}{2}\) oraz \(y=-1\) otrzymamy:
$$y=-3x+b \\
-1=-3\cdot(-\frac{21}{2})+b \\
-1=\frac{63}{2}+b \\
-1=31\frac{1}{2}+b \\
b=-32\frac{1}{2}$$
To oznacza, że nasza prosta \(BD\) wyraża się równaniem: \(y=-3x-32\frac{1}{2}\).
Zadanie 32. (4pkt) W ciągu arytmetycznym \((a_{1}, a_{2},...,a_{39},a_{40})\) suma wyrazów tego ciągu o numerach parzystych jest równa \(1340\), a suma wyrazów ciągu o numerach nieparzystych jest równa \(1400\). Wyznacz ostatni wyraz tego ciągu arytmetycznego.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz dowolne równanie z dwiema niewiadomymi, które wynika z treści zadania np. \(\frac{a_{2}+a_{40}}{2}\cdot20=1340\) lub \(\frac{a_{1}+a_{39}}{2}\cdot20=1400\) lub \(\frac{a_{1}+a_{1}+19\cdot2r}{2}\cdot20=1400\) lub inne podobne.
2 pkt
• Gdy zapiszesz dwa równania z tymi samymi dwiema niewiadomymi.
3 pkt
• Gdy obliczysz różnicę ciągu (patrz: Krok 1.) oraz wartość pierwszego wyrazu (patrz: Krok 3.).
ALBO
• Gdy otrzymany końcowy wynik jest niepoprawny ze względu na błędy rachunkowe.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie różnicy ciągu arytmetycznego.
Z treści zadania wynika, że:
$$a_{2}+a_{4}+a_{6}+...+a_{38}+a_{40}=1340 \\
\text{oraz} \\
a_{1}+a_{3}+a_{5}+...+a_{37}+a_{39}=1400$$
Powstały nam więc tak jakby dwa oddzielne ciągi arytmetyczne, każdy składający się z 20-stu wyrazów.
Jak dobrze się przyjrzymy to zauważymy, że każdy wyraz pierwszego ciągu jest o \(r\) większy od analogicznego wyrazu z ciągu drugiego, bo przecież:
$$a_{2}=a_{1}+r \\
a_{4}=a_{3}+r \\
a_{40}=a_{39}+r$$
Możemy więc ten pierwszy ciąg zapisać jako:
$$(a_{1}+r)+(a_{3}+r)+(a_{5}+r)+...+(a_{37}+r)+(a_{39}+r)=1340 \\
\text{czyli:} \\
a_{1}+a_{3}+a_{5}+...+a_{37}+a_{39}+20r=1340$$
Skoro suma \(a_{1}+a_{3}+a_{5}+...+a_{37}+a_{39}\) jest równa \(1400\), to podstawiając to do powyższego równania otrzymamy:
$$1400+20r=1340 \\
20r=-60 \\
r=-3$$
Krok 2. Obliczenie sumy wszystkich wyrazów ciągu arytmetycznego.
Skoro suma wyrazów parzystych jest równa \(1340\), a suma wyrazów nieparzystych jest równa \(1400\), to suma wszystkich wyrazów naszego całego czterdziesto-wyrazowego ciągu wynosi:
$$S_{40}=1340+1400 \\
S_{40}=2740$$
Krok 3. Obliczenie wartości pierwszego wyrazu.
Skorzystamy teraz ze wzoru na sumę \(n\)-tych wyrazów ciągu arytmetycznego:
$$S_{n}=\frac{a_{1}+a_{n}}{2}\cdot n \\
S_{40}=\frac{a_{1}+a_{40}}{2}\cdot40$$
Wiemy już, że \(S_{40}=2740\) oraz że \(r=-3\). Dodatkowo wartość \(a_{40}\) możemy rozpisać jako \(a_{1}+39r\). To sprawia, że:
$$S_{40}=\frac{a_{1}+a_{1}+39r}{2}\cdot40 \\
2740=\frac{a_{1}+a_{1}+39\cdot(-3)}{2}\cdot40 \\
2740=(a_{1}+a_{1}+(-117))\cdot20 \\
137=2a_{1}-117 \\
2a_{1}=254 \\
a_{1}=127$$
Krok 4. Obliczenie wartości czterdziestego wyrazu.
Skoro \(a_{1}=127\) oraz \(r=-3\), to korzystając z tego, że \(a_{40}=a_{1}+39r\) otrzymamy:
$$a_{40}=a_{1}+39r \\
a_{40}=127+39\cdot(-3) \\
a_{40}=127-117 \\
a_{40}=10$$
Zadanie 33. (4pkt) Środek okręgu leży w odległości \(10cm\) od cięciwy tego okręgu. Długość tej cięciwy jest o \(22cm\) większa od promienia tego okręgu. Oblicz promień tego okręgu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz poprawną zależność między promieniem i długością cięciwy np. że cięciwa ma długość \(r+22\) (patrz: Krok 1.).
ALBO
• Gdy dostrzeżesz np. na rysunku pomocniczym, że powstanie trójkąt prostokątny w którym przeciwprostokątną jest promień, a przyprostokątnymi są odcinek o długości \(10\) oraz połowa długości cięciwy (patrz: Krok 1.).
2 pkt
• Gdy poprawnie ułożysz równanie z wykorzystaniem Twierdzenia Pitagorasa, ale będą w nim dwie niewiadome np. \(10^2+\left(\frac{x}{2}\right)^2=r^2\) i na tym zakończysz zadanie.
3 pkt
• Gdy poprawnie ułożysz równanie z wykorzystaniem Twierdzenia Pitagorasa w którym będzie tylko jedna niewiadoma (patrz: Krok 3.) i na tym zakończysz zadanie.
ALBO
• Gdy otrzymany końcowy wynik jest niepoprawny ze względu na błędy rachunkowe.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować tę sytuację, tak aby mieć lepszy ogląd całej sytuacji:
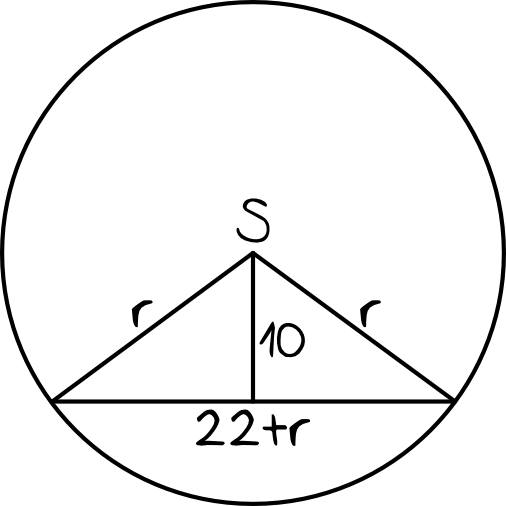
Patrząc się na rysunek widzimy, że powstał nam trójkąt, który jest równoramienny. Skąd wiadomo, że jest on równoramienny? Po prostu jego ramiona są promieniami naszego okręgu, czyli mają jednakową miarę.
Teraz przeanalizujmy odcinek, który łączy środek okręgu i cięciwę. Zgodnie z treścią zadania ma on długość równą \(10\). Z podstaw geometrii wiemy, że odległość z punktu do prostej jest zawsze linią prostopadłą do prostej, nie ma innej możliwości. To sprawia, że ten omawiany odcinek jest tak naprawdę wysokością naszego trójkąta równoramiennego.
Z własności trójkątów równoramiennych wiemy, że wysokość takiego trójkąta dzieli podstawę na dwie równe części, czyli powstaje nam taki oto trójkąt prostokątny:
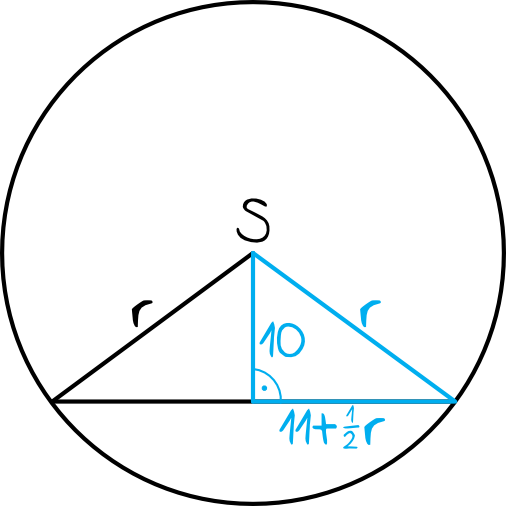
Krok 2. Ułożenie równania kwadratowego.
Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$\left(11+\frac{1}{2}r\right)^2+10^2=r^2 \\
121+11r+\frac{1}{4}r^2+100=r^2 \\
\frac{1}{4}r^2+11r+221=r^2 \quad\bigg/\cdot4 \\
r^2+44r+884=4r^2 \\
-3r^2+44r+884=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego i wyznaczenie długości promienia okręgu.
Współczynniki: \(a=-3,\;b=44,\;c=884\)
$$Δ=b^2-4ac=44^2-4\cdot(-3)\cdot884=1936+10608=12544 \\
\sqrt{Δ}=\sqrt{12544}=112$$
$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-44-112}{2\cdot(-3)}=\frac{-156}{-6}=26 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-44+112}{2\cdot(-3)}=\frac{68}{-6}=-11\frac{1}{3}$$
Otrzymaliśmy dwie możliwości długości promienia, ale jedną z nich musimy odrzucić, bo promień nie może mieć ujemnej długości. W związku z tym jedyną poprawną odpowiedzią będzie \(r=26\).
Zadanie 34. (5pkt) Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest równa \(12\) (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt \(α\) taki, że \(tgα=\frac{2}{\sqrt{5}}\). Oblicz objętość tego ostrosłupa.
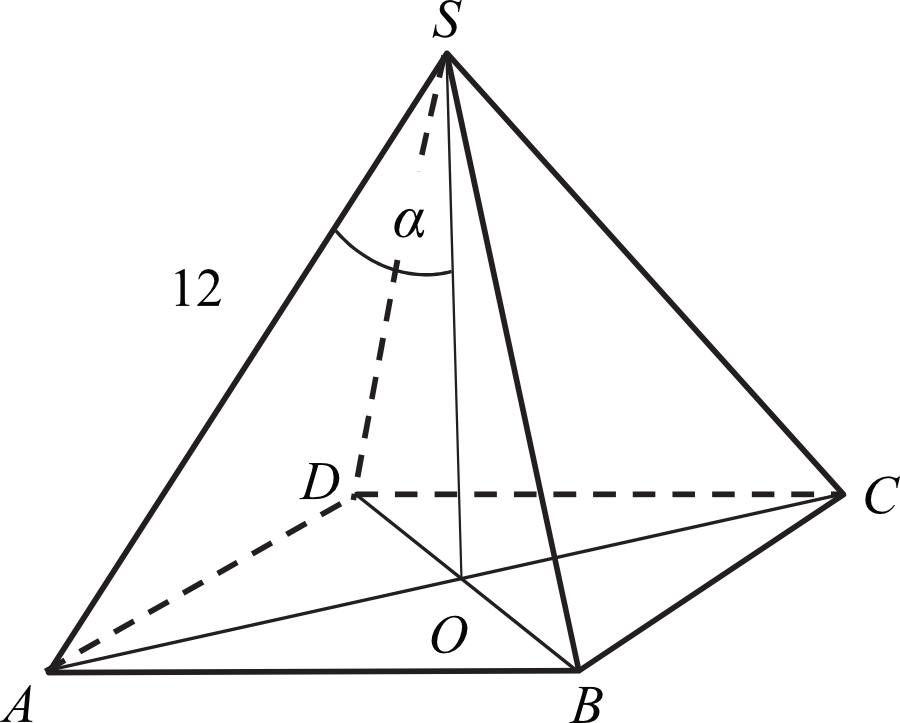
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz jakąkolwiek poprawną zależność np. \(\frac{sinα}{cosα}=\frac{2}{\sqrt{5}}\) (patrz: Krok 2.) lub \(\frac{|AO|}{|SO|}=\frac{2}{\sqrt{5}}\) lub \(|AO|^2+|SO|^2=12^2\) lub jakąś inną podobną.
2 pkt
• Gdy doprowadzisz równanie trygonometryczne do postaci w której wystąpi tylko jedna funkcja trygonometryczna (patrz: Krok 2.).
ALBO
• Gdy zapiszesz dwa równania z niewiadomymi \(a\) oraz \(H\).
3 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 3.).
ALBO
• Gdy obliczysz długość przekątnej podstawy (patrz: Krok 4.).
ALBO
• Gdy obliczysz długość krawędzi podstawy (patrz: Krok 5.).
4 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 3.) oraz jedną z dwóch długości: przekątną podstawy (patrz: Krok 4.) lub długość krawędzi podstawy (patrz: Krok 5.).
ALBO
• Gdy otrzymany końcowy wynik jest niepoprawny ze względu na błędy rachunkowe.
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Omówienie sytuacji z treści zadania.
Na początek warto zwrócić uwagę na to, że nasz ostrosłup jest prawidłowy, czyli w podstawie ma figurę foremną. Skoro jest to ostrosłup prawidłowy czworokątny, to w tym konkretnym przypadku będziemy mieć w podstawie kwadrat.
Spójrzmy teraz na trójkąt \(AOS\). Jest to trójkąt prostokątny na który składa się połowa przekątnej kwadratu, wysokość ostrosłupa oraz krawędź boczna ostrosłupa. Naszym zadaniem będzie tak naprawdę poznanie długości jednej i drugiej przyprostokątnej tego trójkąta (poznanie dolnej przyprostokątnej doprowadzi nas do poznania długości krawędzi podstawy, no a wysokość jest sama w sobie niezbędna do obliczenia objętości).
Podaną mamy wartość tangensa kąta \(α\) i długość przeciwprostokątnej, która jest równa \(12\). Cała trudność tego zadania opiera się na tym, że tangens odpowiada przecież za stosunek długości przyprostokątnych (czyli tych boków, które szukamy) i nie jest on w żaden sposób powiązany z przeciwprostokątną. Gdybyśmy mieli podaną wartość np. cosinusa zamiast tangensa, to wtedy błyskawicznie obliczylibyśmy sobie wysokość bryły. Nic jednak nie stoi na przeszkodzie, by tangensa zamienić na cosinusa i to będzie nasz kolejny krok.
Krok 2. Wyznaczenie wartości \(cosα\).
Z własności funkcji trygonometrycznych wiemy, że \(tgα=\frac{sinα}{cosα}\). Wiemy też z jedynki trygonometrycznej, że \(sin^2α+cos^2α=1\). W związku z tym możemy przystąpić do zamiany tangensa na cosinusa:
$$tgα=\frac{2}{\sqrt{5}} \\
\frac{sinα}{cosα}=\frac{2}{\sqrt{5}} \\
sinα=\frac{2}{\sqrt{5}}cosα$$
Podstawiając teraz wyznaczonego sinusa do jedynki trygonometrycznej otrzymamy:
$$sin^2α+cos^2α=1 \\
\left(\frac{2}{\sqrt{5}}cosα\right)^2+cos^2α=1 \\
\frac{4}{5}cos^2α+cos^2α=1 \\
\frac{9}{5}cos^2α=1 \quad\bigg/\cdot\frac{5}{9} \\
cos^2α=\frac{5}{9} \\
cosα=\frac{\sqrt{5}}{3} \quad\lor\quad cosα=-\frac{\sqrt{5}}{3}$$
Nad otrzymanymi wynikami musimy się jeszcze pochylić, zastanawiając się nad tym, czy przypadkiem któregoś cosinusa nie trzeba odrzucić. Co prawda nie mamy wprost podane w treści zadania, że \(α\) jest kątem ostrym (gdyby tak było, to ujemne rozwiązanie trzeba odrzucić), ale wiemy że tangens był wartością dodatnią, czyli \(α\) rzeczywiście musi być kątem ostrym. Stąd też ujemnego cosinusa możemy odrzucić i zostaje nam, że \(cosα=\frac{\sqrt{5}}{3}\).
Krok 3. Obliczenie długości wysokości ostrosłupa.
Teraz sprawa z obliczeniem wysokości ostrosłupa jest już bardzo prosta, bowiem korzystając z cosinusa możemy zapisać, że:
$$cosα=\frac{H}{12} \\
\frac{\sqrt{5}}{3}=\frac{H}{12} \\
H=\frac{12\sqrt{5}}{3} \\
H=4\sqrt{5}$$
Krok 4. Obliczenie długości przekątnej podstawy.
W trójkącie \(AOS\) nasza dolna przyprostokątna \(AO\) ma długość równą połowie przekątnej podstawy. Wyznaczmy więc najpierw długość tej przyprostokątnej \(AO\), a potem obliczymy długość całej przekątnej \(AC\).
Do obliczenia długości \(AO\) możemy skorzystać albo z Twierdzenia Pitagorasa (bo znamy już długości dwóch boków tego trójkąta), albo nawet z podanego tangensa (bo znamy już długość jednej przyprostokątnej). Korzystając więc z tangensa otrzymamy:
$$tgα=\frac{|AO|}{H} \\
\frac{2}{\sqrt{5}}=\frac{|AO|}{4\sqrt{5}} \\
\frac{8\sqrt{5}}{\sqrt{5}}=|AO| \\
|AO|=8$$
Odcinek \(AO\) jest połową przekątnej naszej podstawy, zatem cała przekątna będzie mieć długość:
$$|AC|=2\cdot8 \\
|AC|=16$$
Krok 5. Obliczenie długości krawędzi podstawy.
W podstawie bryły jest kwadrat, bo ostrosłup jest ostrosłupem prawidłowym czworokątnym. Z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). Skoro więc przekątna kwadratu ma długość \(16\), to:
$$a\sqrt{2}=16 \\
a=\frac{16}{\sqrt{2}} \\
a=\frac{16\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a=\frac{16\sqrt{2}}{2} \\
a=8\sqrt{2}$$
Krok 6. Obliczenie pola podstawy.
W podstawie jest kwadrat o boku \(a=8\sqrt{2}\), zatem pole podstawy będzie równe:
$$P_{p}=(8\sqrt{2})^2 \\
P_{p}=64\cdot2 \\
P_{p}=128$$
Krok 7. Obliczenie objętości ostrosłupa.
Wiedząc już, że \(P_{p}=128\) oraz że \(H=4\sqrt{5}\) bez problemu obliczymy objętość ostrosłupa:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot128\cdot4\sqrt{5} \\
V=\frac{512\sqrt{5}}{3} \\
V=170\frac{2}{3}\sqrt{5}$$