Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Symetria w układzie współrzędnych. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Punkt \(P\) jest symetryczny do punktu \(A=(\sqrt{5};\sqrt{3})\) względem osi igreków. To oznacza, że punkt \(P\) ma współrzędne:
Zadanie 2. (1pkt) Punkt \(B\) jest symetryczny do punktu \(P=(-200;\sqrt{51})\) względem osi iksów. To oznacza, że punkt \(B\) znajdzie się w:
Zadanie 3. (1pkt) Punkt \(A\) jest symetryczny do punktu \(P=(4;2)\) względem prostej \(y=5\). To oznacza, że:
Zadanie 4. (1pkt) Przez odcinek \(AB\), gdzie \(A=(-3;7)\) oraz \(B=(1;-5)\) poprowadzono symetralną, która przecina odcinek \(AB\) w punkcie \(S\). Współrzędne tego punktu to:
Zadanie 5. (1pkt) 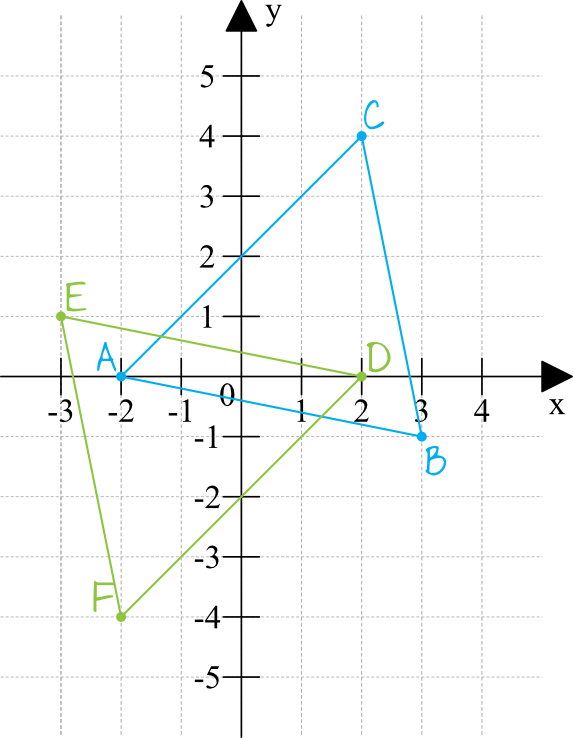
Na rysunku zaznaczono dwa trójkąty, które są symetryczne do siebie względem:
Zadanie 6. (1pkt) Dany jest odcinek \(AB\), gdzie \(A=(-3;\sqrt{3})\) oraz \(B=(3;-\sqrt{3})\). Symetria odcinka \(AB\) względem osi iksów da nam taki sam kształt odcinka, jak symetria odcinka \(AB\) względem igreków.
Zadanie 7. (1pkt) Para punktów \(A=(-6;\sqrt{2})\) oraz \(A'=(0;\sqrt{2})\) jest symetryczna do siebie względem prostej \(y=-3\).
Zadanie 8. (1pkt) Dany jest okrąg o środku \(S=(4;3)\), który przechodzi przez punkt \(A=(7;1)\). Zadaniem dzieci jest teraz znalezienie obrazu symetrii tego okręgu względem osi igreków. Jaś twierdzi, że obrazem tej symetrii będzie okrąg o promieniu \(\sqrt{13}\), który swój środek ma w punkcie \(S=(-4;3)\). Małgosia uważa, że owszem środek tego okręgu byłby w punkcie \(S=(-4;3)\), ale jej zdaniem jest zbyt mało informacji byśmy taką symetrię mogli wykonać. Małgosia uważa, że symetria okręgu (lub koła) jest możliwa tylko i wyłącznie wtedy, gdy znamy współrzędne trzech punktów, które należą do okręgu. Kto ma rację?
Zadanie 9. (1pkt) Przekształcając punkt \(A=(-1;2)\) względem punktu \(S=(4;4)\) otrzymamy punkt:
Zadanie 10. (1pkt) Dany jest równoległobok \(ABCD\) w którym punkty \(A=(2;1)\) oraz \(B=(7;2)\) tworzą dłuższy bok tej figury. Punkt \(S=(5;3)\) jest środkiem symetrii tego równoległoboku. Jeżeli punkt \(D\) tworzy z punktem \(A\) krótszy bok równoległoboku to: