Matura próbna z matematyki (poziom podstawowy) - Listopad 2009
Arkusz maturalny zawiera 25 zadań zamkniętych oraz 9 zadań otwartych. Łącznie do zdobycia jest 50 punktów, a sugerowany maksymalny czas rozwiązywania to 170 minut.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
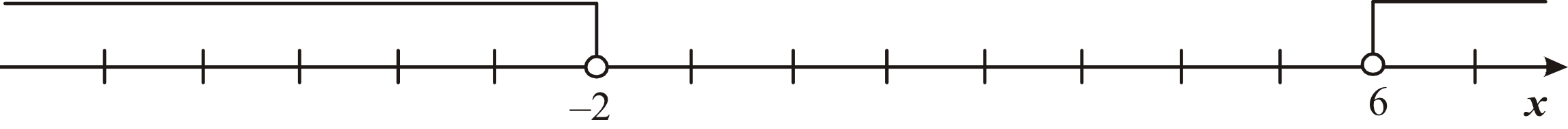
Zadanie 2. (1pkt) Na seans filmowy sprzedano \(280\) biletów, w tym \(126\) ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
Zadanie 3. (1pkt) \(6\%\) liczby \(x\) jest równe \(9\). Wtedy:
Zadanie 4. (1pkt) Iloraz \(32^{-3}:\left(\frac{1}{8}\right)^4\) jest równy:
Zadanie 5. (1pkt) O liczbie \(x\) wiadomo, że \(\log_{3}x=9\). Zatem:
Zadanie 6. (1pkt) Wyrażenie \(27x^3+y^3\) jest równe iloczynowi:
Zadanie 7. (1pkt) Dane są wielomiany \(W(x)=x^3-3x+1\) oraz \(V(x)=2x^3\). Wielomian \(W(x)\cdot V(x)\) jest równy:
Zadanie 8. (1pkt) Wierzchołek paraboli o równaniu \(y=-3(x+1)^2\) ma współrzędne:
Zadanie 9. (1pkt) Do wykresu funkcji \(f(x)=x^2+x-2\) należy punkt:
Zadanie 10. (1pkt) Rozwiązaniem równania \(\frac{x-5}{x+3}=\frac{2}{3}\) jest liczba:
Zadanie 11. (1pkt) Zbiór rozwiązań nierówności \((x+1)(x-3)\gt0\) przedstawiony jest na rysunku:
Zadanie 12. (1pkt) Dla \(n=1,2,...\) ciąg \((a_{n})\) jest określony wzorem \(a_{n}=(-1)^n\cdot(3-n)\). Wtedy:
Zadanie 13. (1pkt) W ciągu arytmetycznym trzeci wyraz jest równy \(14\), a jedenasty jest równy \(34\). Różnica tego ciągu jest równa:
Zadanie 14. (1pkt) W ciągu geometrycznym \((a_{n})\) dane są: \(a_{1}=32\) i \(a_{4}=-4\). Iloraz tego ciągu jest równy:
Zadanie 15. (1pkt) Kąt \(α\) jest ostry i \(sinα=\frac{8}{9}\). Wówczas \(cosα\) jest równy:
Zadanie 16. (1pkt) Dany jest trójkąt prostokątny (patrz rysunek).
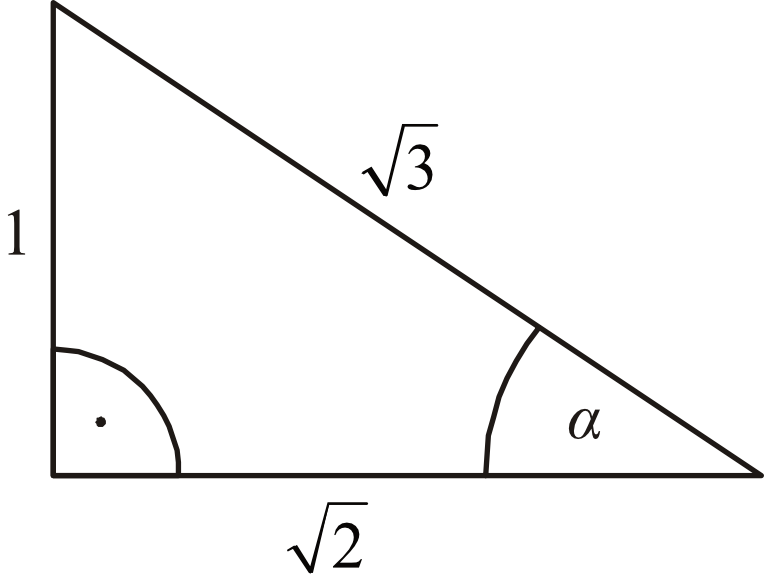
Wtedy \(tgα\) jest równy:
Zadanie 17. (1pkt) W trójkącie równoramiennym \(ABC\) dane jest \(|AC|=|BC|=7\) oraz \(|AB|=12\). Wysokość opuszczona z wierzchołka \(C\) jest równa:
Zadanie 18. (1pkt) Oblicz długość odcinka \(AE\) wiedząc, że \(AB||CD\) i \(|AB|=6\), \(|AC|=4\), \(|CD|=8\).
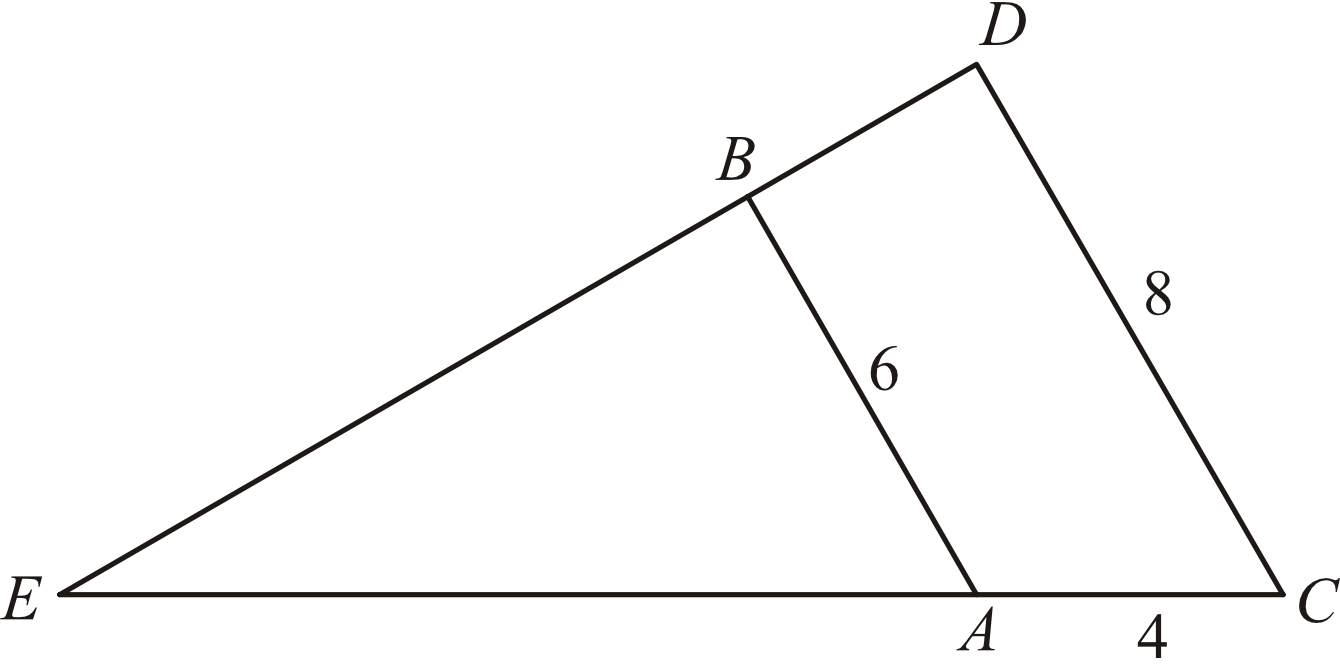
Zadanie 19. (1pkt) Dane są punkty \(A=(-2,3)\) oraz \(B=(4,6)\). Długość odcinka \(AB\) jest równa:
Zadanie 20. (1pkt) Promień okręgu o równaniu \((x-1)^2+y^2=16\) jest równy:
Zadanie 21. (1pkt) Wykres funkcji liniowej określonej wzorem \(f(x)=3x+2\) jest prostą prostopadłą do prostej:
Zadanie 22. (1pkt) Prosta o równaniu \(y=-4x+(2m-7)\) przechodzi przez punkt \(A=(2,-1)\). Wtedy:
Zadanie 23. (1pkt) Pole powierzchni całkowitej sześcianu jest równe \(150cm^2\). Długość krawędzi tego sześcianu jest równa:
Zadanie 24. (1pkt) Średnia arytmetyczna pięciu liczb: \(5, x, 1, 3, 1\) jest równa \(3\). Wtedy:
Zadanie 25. (1pkt) Wybieramy liczbę \(a\) ze zbioru \(A=\{2,3,4,5\}\) oraz liczbę \(b\) ze zbioru \(B=\{1,4\}\). Ile jest takich par \((a,b)\), że iloczyn \(a\cdot b\) jest liczbą nieparzystą?
Zadanie 26. (2pkt) Rozwiąż nierówność \(x^2-3x+2\le0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz miejsca zerowe, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe funkcji (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).
Wyjaśnienie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Skorzystamy tutaj z tradycyjnej metody delty:
Współczynniki: \(a=1,\;b=-3,\;c=2\)
$$Δ=b^2-4ac=(-3)^2-4\cdot1\cdot2=9-8=1 \\
\sqrt{Δ}=\sqrt{1}=1$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-3)-1}{2\cdot1}=\frac{3-1}{2}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-3)+1}{2\cdot1}=\frac{3+1}{2}=2$$
Krok 2. Szkicowanie wykresu paraboli.
Ramiona paraboli będą skierowane do góry, bo współczynnik \(a\) jest dodatni. Zaznaczamy na osi obliczone przed chwilą miejsca zerowe i przystępujemy do rysowania paraboli. Pamiętaj, by kółka przy miejscach zerowych były zamalowane, bo w nierówności wystąpił znak \(\le\).

Krok 3. Odczytanie rozwiązania.
Interesują nas argumenty, dla których nierówność przyjmuje wartości mniejsze lub równe zero. W związku z tym: \(x\in\langle1;2\rangle\).
Zadanie 27. (2pkt) Rozwiąż równanie \(x^3-7x^2+2x-14=0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy pogrupujesz wyrazy i wyłączysz odpowiednie czynniki przed nawias w taki sposób, że w nawiasach jest jednakowa wartość, dzięki której można szybko przejść do postaci iloczynowej albo wręcz doprowadzisz równanie do postaci iloczynowej (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wyłączenie odpowiednich czynników przed nawias i zapisanie równania w postaci iloczynowej.
Musimy wyłączyć odpowiednie czynniki przed nawias w taki sposób, by wartości w dwóch nawiasach były identyczne - to pozwoli nam przekształcić to równanie na postać iloczynową.
$$x^3-7x^2+2x-14=0 \\
x^2(x-7)+2(x-7)=0 \\
(x^2+2)(x-7)=0$$
Krok 2. Wyznaczenie rozwiązań z postaci iloczynowej.
Mamy już równanie w postaci iloczynowej. Aby było ono równe zero, to któryś z nawiasów musi "zerować" to równanie, tak więc:
$$x^2+2=0 \quad\lor\quad x-7=0 \\
x^2=-2 \quad\lor\quad x=7$$
Z pierwszej części tego równania nie wyznaczymy żadnych rozwiązań, bo wartość \(x^2\) jest zawsze dodatnia. To oznacza, że jedynym rozwiązaniem tego równania jest \(x=7\).
Zadanie 28. (2pkt) W układzie współrzędnych na płaszczyźnie punkty \(A=(2,5)\) i \(C=(6,7)\) są przeciwległymi wierzchołkami kwadratu \(ABCD\). Wyznacz równanie prostej \(BD\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz współrzędne przecięcia się przekątnych (patrz: Krok 2.).
ALBO
• Gdy wyznaczysz wzór prostej przechodzącej przez punkty \(A\) oraz \(C\) (patrz: Krok 3.).
ALBO
• Gdy rozwiązanie zadania nie jest do końca poprawne, ale wynika to z błędu rachunkowego.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Na początku dobrze jest zaznaczyć sobie w układzie współrzędnych punkty \(A\) oraz \(C\), a także prostą na której znajdą się brakujące punkty \(B\) oraz \(D\). I tu pierwsze bardzo ważne spostrzeżenie - przekątne kwadratu przecinają się dokładnie w połowie swojej długości, a więc nasza prosta będzie na pewno przechodzić przez punkt \(S\), który jest środkiem odcinka \(AC\).
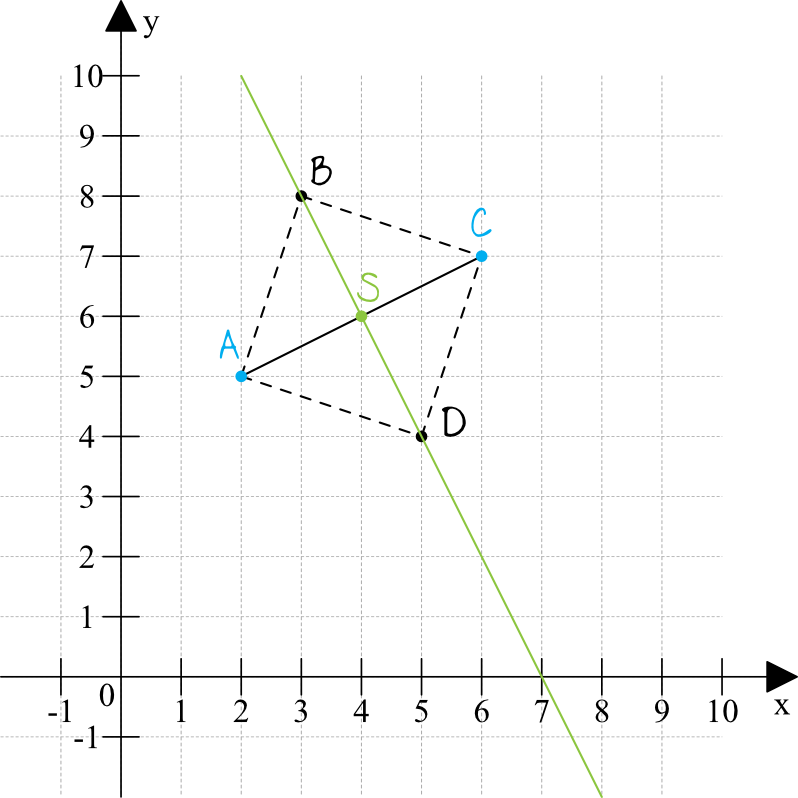
Krok 2. Obliczenie współrzędnych punktu \(S\).
Skorzystamy ze wzorów, które dostępne są w tablicach matematycznych:
$$x_{S}=\frac{x_{A}+x_{C}}{2}=\frac{2+6}{2}=\frac{8}{2}=4 \\
y_{S}=\frac{y_{A}+y_{C}}{2}=\frac{5+7}{2}=\frac{12}{2}=6 \\
S=(4;6)$$
Krok 3. Wyznaczenie wzoru prostej \(AC\).
Nasz plan działania jest dość prosty. Wyznaczymy sobie wzór prostej \(AC\), a następnie wzór prostej prostopadłej, która będzie przechodzić przez punkt \(S\). To właśnie ta prosta prostopadła jest przez nas poszukiwana. Prosta \(AC\) przyjmuje postać \(y=ax+b\), więc możemy podstawić pod ten wzór najpierw współrzędne punktu \(A\), następnie punktu \(C\) i w ten sposób stworzymy prosty układ równań:
\begin{cases}
5=2a+b \\
7=6a+b
\end{cases}
Możemy zastosować tu metodę podstawiania, przyjmując z pierwszego równania \(b=5-2a\), jednak znacznie prościej i szybciej będzie po prostu odjąć to równanie stronami. Otrzymamy wtedy:
$$-2=-4a \quad\bigg/:(-4) \\
a=\frac{1}{2}$$
Możemy jeszcze wyznaczyć współczynnik \(b\) tej prostej, choć nie będzie nam on już potrzebny do dalszych obliczeń. Podstawiamy obliczoną przed chwilą wartość współczynnika \(a\) do wybranego równania, otrzymując:
$$5=2\cdot\frac{1}{2}+b \\
5=1+b \\
b=4$$
Wzór prostej przechodzącej przez punkty \(A\) i \(C\) to \(y=\frac{1}{2}+4\).
Krok 4. Wyznaczenie wzoru prostej \(BD\).
Prosta \(BD\) będzie na pewno prostopadła do prostej \(AC\) oraz będzie przechodzić przez punkt \(S\). Aby dwie proste były względem siebie prostopadłe to iloczyn ich współczynników kierunkowych \(a\) musi być równy \(-1\). Skoro pierwsza prosta ma współczynnik kierunkowy równy \(\frac{1}{2}\) to druga musi mieć:
$$a\cdot\frac{1}{2}=-1 \\
a=-2$$
Wiemy już, że prosta \(BD\) przyjmuje postać \(y=-2x+b\). Brakuje nam jeszcze tylko współczynnika \(b\). Wyznaczymy go podstawiając współrzędne punktu \(S\), przez który musi ta prosta przechodzić, stąd też:
$$6=-2\cdot4+b \\
6=-8+b \\
b=14$$
Wzór prostej \(BD\) to w takim razie \(y=-2x+14\).
Zadanie 29. (2pkt) Kąt \(α\) jest ostry oraz \(tgα=\frac{4}{3}\). Oblicz \(sinα+cosα\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy rozwiązujesz zadanie metodą graficzną (rysując trójkąt prostokątny) i źle zaznaczysz kąt \(α\) lub źle zapiszesz stosunek długości boków w danej funkcji trygonometrycznej.
1 pkt
• Gdy przekształcisz to wyrażenie z użyciem jedynki trygonometrycznej i z wykorzystaniem własności \(tgα=\frac{sinα}{cosα}\), ale popełnisz gdzieś błąd rachunkowy lub na tym poprzestaniesz rozwiązanie zadania.
ALBO
• Gdy podejmiesz próbę rozwiązania tego zadania rysując trójkąt prostokątny, ale np. pomylisz się przy obliczaniu długości przeciwprostokątnej.
ALBO
• Gdy w trakcie obliczeń wartości sinusa lub cosinusa nie odrzucisz ujemnego rozwiązania.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wyznaczenie wzoru na wartość sinusa.
Z funkcji trygonometrycznych wiemy, że \(tgα=\frac{sinα}{cosα}\). Podstawmy więc znaną nam wartość tangensa i spróbujmy wyznaczyć z niej wartość sinusa:
$$\frac{sinα}{cosα}=\frac{4}{3} \\
sinα=\frac{4}{3}cosα$$
Krok 2. Obliczenie wartości cosinusa.
Tym razem skorzystamy ze wzoru na jedynkę trygonometryczną, dzięki któremu obliczymy dokładną wartość cosinusa.
$$sin^2α+cos^2α=1$$
Podstawiając do tego wzoru wyznaczoną wartość sinusa z poprzedniego kroku otrzymamy:
$$\left(\frac{4}{3}cosα\right)^2+cos^2α=1 \\
\frac{16}{9}cos^2α+cos^2α=1 \\
\frac{25}{9}cos^2α=1 \quad\bigg/\cdot\frac{9}{25} \\
cos^2α=\frac{9}{25} \\
cosα=\frac{3}{5} \quad\lor\quad cosα=-\frac{3}{5}$$
Wartość ujemną odrzucamy, bowiem w treści zadania mowa jest o kącie ostrym, a dla kątów ostrych cosinus jest dodatni.
Krok 3. Obliczenie wartości sinusa.
Obliczoną wartość cosinusa możemy podstawić do wzoru wyprowadzonego w pierwszym kroku, tak więc:
$$sinα=\frac{4}{3}cosα \\
sinα=\frac{4}{3}\cdot\frac{3}{5} \\
sinα=\frac{12}{15}=\frac{4}{5}$$
Krok 4. Obliczenie wartości wyrażenia \(sinα+cosα\).
Znamy już wartość sinusa i cosinusa, tak więc:
$$sinα+cosα=\frac{4}{5}+\frac{3}{5}=\frac{7}{5}=1\frac{2}{5}$$
Zadanie 30. (2pkt) Wykaż, że dla kazdego \(m\) ciąg \(\left(\frac{m+1}{4},\frac{m+3}{6},\frac{m+9}{12}\right)\) jest arytmetyczny.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie zapiszesz relację między trzema wyrazami ciągu i na tej podstawie ułożysz równanie (patrz: Krok 1.).
ALBO
• Gdy doprowadzisz do rozwiązania otrzymanego równania (patrz: Krok 2.), ale nie wyciągniesz z niego żadnych wniosków.
2 pkt
• Gdy udowodnisz to zadanie np. korzystając z własności ciągów arytmetycznych (tak jak w przykładzie), albo udowadniając że ciąg jest arytmetyczny bo różnica między poszczególnymi wyrazami jest jednakowa.
Wyjaśnienie:
Krok 1. Zapisanie równania na podstawie danych z treści zadania.
Zgodnie z własnościami ciągów artmetycznych dla trzech kolejno wypisanych wyrazów ciągu prawdziwa będzie zależność:
$$a_{2}=\frac{a_{1}+a_{3}}{2}$$
Z racji tego, że dużo w tym zadaniu będzie działań na ułamkach, to może od razu pomnóżmy sobie obie strony tej zależności przez \(2\), tak aby ułatwić sobie obliczenia w dalszej fazie, zatem:
$$2a_{2}=a_{1}+a_{3}$$
Podstawiając do naszego wzoru dane z treści zadania otrzymamy:
$$2\cdot\frac{m+3}{6}=\frac{m+1}{4}+\frac{m+9}{12}$$
Krok 2. Rozwiązanie powstałego równania.
Możemy to równanie rozwiązać w dowolny sposób, ale chyba najprościej będzie od razu pozbyć się ułamków i wymnożyć obie strony przez \(12\).
$$2\cdot\frac{m+3}{6}=\frac{m+1}{4}+\frac{m+9}{12} \quad\bigg/\cdot12 \\
2\cdot(2m+6)=(3m+3)+(m+9) \\
4m+12=4m+12$$
Krok 3. Interpretacja otrzymanego wyniku.
Po obu stronach równania otrzymaliśmy tą samą wartość. Jest to więc równanie tożsamościowe, czyli takie które spełnia każda liczba. W związku z tym otrzymany wynik kończy nasze dowodzenie, bo w ten sposób udało nam się dowieść, że ciąg jest arytmetyczny dla każdego \(m\).
Zadanie 31. (2pkt) Trójkąty \(ABC\) i \(CDE\) są równoboczne. Punkty \(A\), \(C\) i \(E\) leżą na jednej prostej. Punkty \(K\), \(L\) i \(M\) są środkami odcinków \(AC\), \(CE\) i \(BD\) (zobacz rysunek). Wykaż, że punkty \(K\), \(L\) i \(M\) są wierzchołkami trójkąta równobocznego.
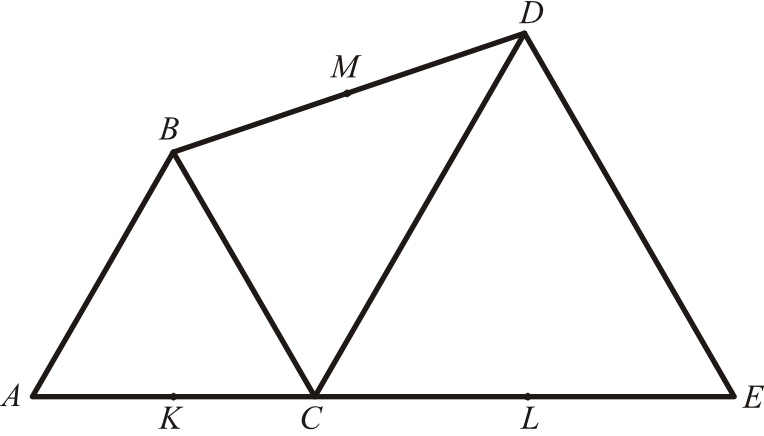
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy zapiszesz (bez udowodnienia), że poszczególne kąty mają 60° i dlatego trójkąt jest równoboczny.
1 pkt
• Gdy udowodnisz równoległość boków \(AB||CD\) albo \(CB||ED\) (patrz: Krok 2.).
ALBO
• Gdy udowodnisz jakąś inną własność (np. omówioną w kroku 2.), ale nie doprowadzisz dowodu do końca.
2 pkt
• Gdy w pełni zakończysz dowodzenie zadania.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Połączmy sobie punkty \(K\), \(L\) oraz \(M\) - tworzą one wierzchołki trójkąta, którego cechę równoboczności musimy udowodnić. Skoro trójkąty \(ABC\) i \(CDE\) są równoboczne, to możemy na rysunek nanieść też ich miary \(60°\).
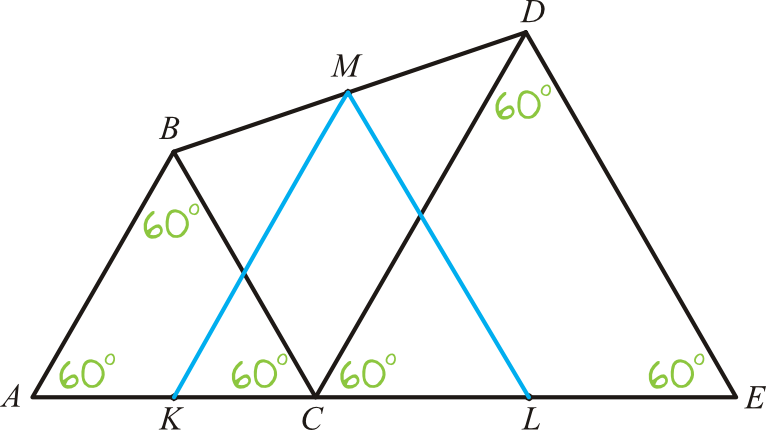
Krok 2. Dostrzeżenie par odcinków równoległych.
Zarówno bok \(AB\) jak i \(CD\) są nachylone do podstawy czworokąta \(AEDB\) pod kątem \(60°\). To oznacza, że te odcinki są względem siebie równoległe, czyli \(AB||CD\).
Punkty \(K\) oraz \(M\) dzielą odcinki łączące te dwie proste równoległe dokładnie w połowie swojej długości, stąd też odcinek \(KM\) jest równoległy do odcinków \(AB\) i \(CD\), a więc i on jest nachylony do podstawy czworokąta pod kątem \(60°\). Ta zależność wynika także z Twierdzenia Talesa. Wiemy już więc, że \(\sphericalangle MKL=60°\).
Analogicznie sytuacja wygląda po drugiej stronie czworokąta. Odcinki \(CB\) oraz \(ED\) są nachylone do podstawy czworokąta pod tym samym kątem \(60°\), są więc względem siebie równoległe. Odcinek \(ML\) jest równoległy względem zarówno odcinka \(CB\) jak i \(ED\) (dokładnie z tego samego powodu o jakim mówiliśmy powyżej, analizując odcinek \(KM\)), a więc \(\sphericalangle MLK=60°\).
Dwa kąty w trójkącie KLM mają miarę \(60°\) więc i trzeci kąt musi mieć \(60°\), czyli jest to trójkąt równoboczny.
Zadanie 32. (5pkt) Uczeń przeczytał książkę liczącą \(480\) stron, przy czym każdego dnia czytał taką samą liczbę stron. Gdyby czytał każdego dnia o \(8\) stron więcej, to przeczytałby tę książkę o \(3\) dni wcześniej. Ile dni czytał tę książkę?
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wprowadzisz sensowne oznaczenia i zapiszesz podstawowe relacje między nimi (patrz: Krok 1.).
2 pkt
• Gdy zapiszesz równanie z którego potem można dokonać obliczenia prowadzące do rozwiązania zadania (patrz: Krok 1.).
3 pkt
• Gdy rozwiążesz otrzymane równanie i doprowadzisz je do postaci ogólnej równania kwadratowego (patrz: Krok 2.).
4 pkt
• Gdy rozwiążesz otrzymane równanie kwadratowe i na tym zakończysz rozwiązywanie zadania (Krok 3.).
ALBO
• Gdy doprowadzisz zadanie do samego końca, ale otrzymany wynik będzie zły jedynie ze względu na błąd rachunkowy popełniony gdzieś w trakcie obliczeń.
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Zapisanie równania na podstawie danych z zadania.
Oznaczmy sobie jako \(x\) liczbę dni jakie zajęło uczniowi czytanie książki. Skoro każdego dnia czytał tyle samo stron, to dziennie czytał ich \(\frac{480}{x}\). Wiemy też, że gdyby czytał o \(8\) stron więcej (czyli gdyby czytał \(\frac{480}{x}+8\)), to czytałby o \(3\) dni krócej (czyli czas czytania wyniósłby \(x-3\)). W takim razie możemy ułożyć następujące równanie:
$$\left(\frac{480}{x}+8\right)\cdot(x-3)=480$$
Krok 2. Rozwiązanie utworzonego równania.
Możemy albo najpierw wymnożyć oba nawiasy przez siebie, a następnie pomnożyć obie strony równania przez \(x\), albo można też od razu pomnożyć obie strony przez \(x\) i dopiero potem wymnożyć przez siebie wyrazy w nawiasach. Obydwie metody są skuteczne, tak więc może zróbmy to po kolei i wymnóżmy poszczególne wyrazy. Otrzymamy wtedy:
$$\require{cancel}
480-\frac{1440}{x}+8x-24=480 \quad\bigg/\cdot x \\
\cancel{480x}-1440+8x^2-24x=\cancel{480x} \\
8x^2-24x-1440=0$$
Możemy jeszcze uprościć to równanie dzieląc wszystko przez \(8\) (nie jest to konieczne, ale dzięki temu będziemy mieć mniejsze liczby w obliczeniach), zatem otrzymamy:
$$x^2-3x-180=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Skorzystamy tutaj z metody delty, tak więc:
Współczynniki: \(a=1,\;b=-3,\;c=-180\)
$$Δ=b^2-4ac=(-3)^2-4\cdot1\cdot(-180)=9-(-720)=9+720=729 \\
\sqrt{Δ}=\sqrt{729}=27$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-3)-27}{2\cdot1}=\frac{3-27}{2}=\frac{-24}{2}=-12 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-3)+27}{2\cdot1}=\frac{3+27}{2}=\frac{30}{2}=15$$
Wartość ujemną oczywiście odrzucamy, tak więc otrzymaliśmy wynik \(x=15\), a to oznacza że uczeń czytał książkę przez \(15\) dni.
Zadanie 33. (4pkt) Punkty \(A=(2,0)\) i \(B=(12,0)\) są wierzchołkami trójkąta prostokątnego \(ABC\) o przeciwprostokątnej \(AB\). Wierzchołek \(C\) leży na prostej \(y=x\). Oblicz współrzędne punktu \(C\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz odpowiednie relacje między długościami boków korzystając z Twierdzenia Pitagorasa, ale nie obliczysz z nich współrzędnych punktu \(C\) i zakończysz na tym zadanie (patrz: Krok 2.).
2 pkt
• Gdy rozpiszesz równanie ułożone na podstawie Twierdzenia Pitagorasa, wykorzystasz wzory na długość odcinka i podstawisz odpowiednie dane z treści zadania (patrz: Krok 2.) ale nie dostrzeżesz tego, że współrzędna "iksowa" punktu \(C\) jest równa współrzędnej "igrekowej".
3 pkt
• Gdy dojdziesz do końca zadania, ale otrzymasz zły wynik w wyniku błędu rachunkowego.
ALBO
• Gdy otrzymane rozwiązanie jest niepełne (np. zawiera tylko jedną z dwóch możliwości).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Zapisanie współrzędnych punktu \(C\).
Każdy punkt w układzie współrzędnych możemy opisać jako \(C=(x;y)\). W treści zadania mamy jednak podaną bardzo ważną informację, która mówi nam że punkt \(C\) leży na prostej \(y=x\). Możemy więc podstawić "iksa" pod drugą współrzędną punktu \(C\), dzięki czemu otrzymamy współrzędne \(C=(x;x)\). To nam bardzo uprości rozwiązanie tego zadania, bo w ten sposób pozbyliśmy się już jednej niewiadomej. Całą resztę możemy już obliczyć z Twierdzenia Pitagorasa.
Krok 2. Obliczenie współrzędnych punktu \(C\) z wykorzystaniem Twierdzenia Pitagorasa.
Długość poszczególnych odcinków (np. odcinka \(AB\)) w układzie współrzędnych możemy opisać wzorem:
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2}$$
W Twierdzeniu Pitagorasa musimy każdą wartość podnieść do kwadratu, więc pierwiastek z powyższego równania zniknie nam w trakcie obliczeń. Przykładowo:
$$|AB|^2=(x_{B}-x_{A})^2+(y_{B}-y_{A})^2$$
Z treści zadania wynika, że przeciwprostokątną jest odcinek \(AB\), tak więc:
$$\color{orange}{|AC|^2}+\color{blue}{|BC|^2}=\color{green}{|AB|^2} \\
\color{orange}{(x_{C}-x_{A})^2+(y_{C}-y_{A})^2}+\color{blue}{(x_{C}-x_{B})^2+(y_{C}-y_{B})^2}=\color{green}{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2}$$
Podstawiamy współrzędne: \(A=(2,0)\), \(B=(12,0)\) oraz \(C=(x;x)\):
$$(x-2)^2+(x-0)^2+(x-12)^2+(x-0)^2=(12-2)^2+(0-0)^2 \\
x^2-4x+4+x^2+x^2-24x+144+x^2=100 \\
4x^2-28x+48=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Korzystając z metody delty otrzymamy:
Współczynniki: \(a=4,\;b=-28,\;c=48\)
$$Δ=b^2-4ac=(-28)^2-4\cdot4\cdot48=784-768=16 \\
\sqrt{Δ}=\sqrt{16}=4$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-28)-4}{2\cdot4}=\frac{28-4}{8}=\frac{24}{8}=3 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-28)+4}{2\cdot4}=\frac{28+4}{8}=\frac{32}{8}=4$$
Krok 4. Ustalenie współrzędnych punktu \(C\).
Nie możemy odrzucić żadnego z otrzymanych rozwiązań równania kwadratowego z trzeciego kroku, a to oznacza że będziemy mieli dwa rozwiązania tego zadania. Zgodnie z tym co sobie zapisaliśmy w pierwszym kroku - współrzędne punktu \(C\) określić możemy jako \((x;x)\), zatem:
$$C=(3;3) \quad\lor\quad C=(4;4)$$
Zadanie 34. (4pkt) Pole trójkąta prostokątnego jest równe \(60cm^2\). Jedna przyprostokątna jest o \(7cm\) dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wprowadzisz sensowne oznaczenia i zapiszesz podstawowe relacje między długościami boków (patrz: Krok 1.).
2 pkt
• Gdy zapiszesz dane w formie układu równań i rozwiążesz ten układ. (patrz: Krok 1. oraz 2.)
3 pkt
• Gdy rozwiążesz powstałe równanie kwadratowe i na tym zakończysz zadanie lub błędnie wywnioskujesz że otrzymany wynik jest już długością przeciwprostokątnej.
ALBO
• Gdy rozwiążesz zadanie do końca, ale otrzymasz zły wynik w wyniku jakiegoś błędu rachunkowego.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Stworzenie układu równań na podstawie danych z treści zadania.
Oznaczmy sobie przyprostokątne jako \(x\) oraz \(y\), a przeciwprostokątną jako \(z\). Ze wzoru na pole trójkąta wiemy, że:
$$P=\frac{1}{2}\cdot x \cdot y \\
60=\frac{1}{2}\cdot x \cdot y \\
x\cdot y=120$$
I to będzie nasze pierwsze równanie.
Z samej treści zadania wynika, że jedna z tych przyprostokątnych jest o \(7cm\) dłuższa od drugiej (nie ma dla nas znaczenia która krótsza, a która dłuższa), czyli:
$$x=y+7$$
I tu mała uwaga: W tym przypadku założyliśmy sobie, że przyprostokątna \(x\) jest dłuższa. Równie dobrze możemy zapisać to jako \(x=y-7\), wtedy to przyprostokątna \(y\) będzie dłuższa. Wbrew pozorom nie ma to dla nas generalnie znaczenia, bo naszym celem i tak jest wyznaczenie długości przeciwprostokątnej.
Z naszych rozważań możemy zbudować następujący układ równań:
\begin{cases}
x\cdot y=120 \\
x=y+7
\end{cases}
Krok 2. Rozwiązanie powstałego układu równań.
Podstawiamy dane z drugiego równania do pierwszego, otrzymując w ten sposób:
$$(y+7)\cdot y=120 \\
y^2+7y-120=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Do obliczenia tego równania skorzystamy z metody delty.
Współczynniki: \(a=1,\;b=7,\;c=-120\)
$$Δ=b^2-4ac=7^2-4\cdot1\cdot(-120)=49-(-480)=49+480=529 \\
\sqrt{Δ}=\sqrt{529}=23$$
$$y_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-7-23}{2\cdot1}=\frac{-30}{2}=-15 \\
y_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-7+23}{2\cdot1}=\frac{16}{2}=8$$
Ujemne rozwiązanie odrzucamy, bo długość odcinka musi być dodatnia. To oznacza, że przyprostokątna \(y=8\). Podstawiając tą wartość do dowolnego z równań możemy szybko wyznaczyć długość także drugiej przyprostokątnej:
$$x=8+7 \\
x=15$$
Krok 4. Obliczenie długości przeciwprostokątnej.
Znając długości dwóch przyprostokątnych możemy za pomocą Twierdzenia Pitagorasa obliczyć długość przeciwprostokątnej, zatem:
$$x^2+y^2=z^2 \\
15^2+8^2=z^2 \\
225+64=z^2 \\
z^2=289 \\
z=17$$