Test

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz poprawne równanie (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.

Krok 1. Ułożenie i rozwiązanie równania.
Naszym zadaniem jest tak naprawdę rozwiązanie i wyciągnięcie wniosków z następującego równania:
$$\frac{3n-1}{2n+5}=\frac{33}{27}$$

To równanie najproście jest rozwiązać mnożąc na krzyż, zatem:
$$27\cdot(3n-1)=33\cdot(2n+5) \\
81n-27=66n+165 \\
15n=192 \\
n=12,8$$

Krok 2. Interpretacja otrzymanego wyniku.
W ciągach \(n\) jest zawsze liczbą naturalną większą od zera. Otrzymany wynik nie jest liczbą naturalną, zatem liczba \(\frac{33}{27}\) nie jest wyrazem tego ciągu (dokładniej rzecz ujmując jest to liczba pomiędzy \(12\)-stym i \(13\)-stym wyrazem).

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz, że ta nierówność nie ma miejsc zerowych, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).

Krok 1. Obliczenie miejsc zerowych wielomianu.
Naszą nierówność obliczymy standardowo metodą delty:
Współczynniki: \(a=-1,\;b=8,\;c=-20\)
$$Δ=b^2-4ac=8^2-4\cdot(-1)\cdot(-20)=64-80=-16$$

Krok 2. Szkicowanie wykresu paraboli.
To, że wyszła nam ujemna delta nie oznacza, że nierówność nie ma rozwiązań lub że w ogóle nie istnieje. Oznacza to tylko tyle, że nie będziemy mieć miejsc zerowych. Parabola będzie mieć ramiona skierowane do dołu (bo współczynnik \(a\) jest ujemny), zatem całość będzie wyglądać mniej więcej w ten sposób:



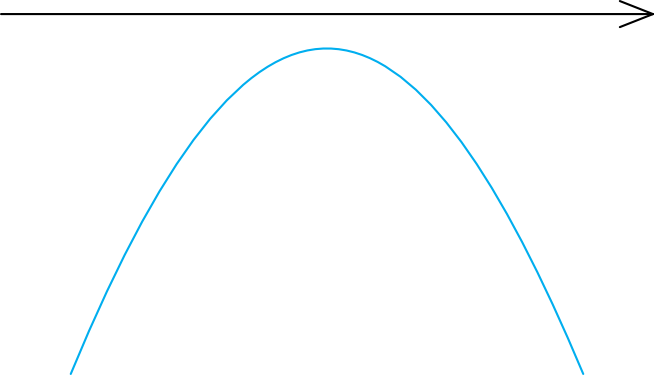
Krok 3. Odczytanie rozwiązania.
Szukamy wartości mniejszych od zera i okazuje się, że nasza cała parabola jest pod osią iksów. To oznacza, że jakiejkolwiek liczby nie podstawimy do nierówności, to otrzymamy zawsze wynik ujemny, zatem rozwiązaniem tej nierówności jest po prostu zbiór liczb rzeczywistych \(x\in\mathbb{R}\).

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość boku \(AB\) (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.

Krok 1. Obliczenie długości boku \(AB\).
Znając współrzędne obydwu punktów możemy obliczyć długość odcinka \(AB\) (czyli długość boku trójkąta):
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2} \\
|AB|=\sqrt{(6-(-2))^2+(2-4)^2} \\
|AB|=\sqrt{8^2+(-2)^2} \\
|AB|=\sqrt{64+4} \\
|AB|=\sqrt{68} \\
|AB|=\sqrt{4\cdot17} \\
|AB|=2\sqrt{17}$$

Krok 2. Obliczenie wysokości trójkąta.
Nasz trójkąt jest trójkątem równobocznym, zatem znając długość boku możemy obliczyć wysokość figury z następującego wzoru:
$$h=\frac{a\sqrt{3}}{2} \\
h=\frac{2\sqrt{17}\cdot\sqrt{3}}{2} \\
h=\sqrt{17}\cdot\sqrt{3} \\
h=\sqrt{51}$$

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy przekształcisz to równanie w taki sposób, że rozbijesz trzynastkę na sumę \(9+4\), ale nie zakończysz dowodzenia.
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.

Aby udowodnić, że nasze wyrażenie jest większe lub równe zero musimy doprowadzić zapis do postaci z potęgowaniem, bowiem jakiejkolwiek liczby byśmy nie podnieśli do potęgi, to będzie ona większa lub równa zero. Będziemy więc chcieli "zwinąć" zapis przy użyciu wzorów skróconego mnożenia. Aby tego dokonać musimy zastosować bardzo sprytny zabieg, a mianowicie musimy rozbić liczbę \(13\) na sumę liczb \(9+4\). Całość będzie wyglądać w następujący sposób:
$$x^2-6x+y^2-4y+13 \\
x^2-6x+9+y^2-4y+4 \\
(x-3)^2+(y-2)^2$$

\((x-3)^2\) jest większe lub równe zero oraz \((y-2)^2\) jest większe lub równe zero. Suma dwóch liczb większych lub równych zero jest także większa lub równa zero i właśnie to musieliśmy udowodnić.

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy dorysujesz przekątną kwadratu i zauważysz, że jej częścią składową jest wysokość trójkąta oraz połowa długości boku tego trójkąta (patrz: Krok 1.).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.

Krok 1. Sporządzenie rysunku pomocniczego.
Jeżeli dorysujemy przekątną kwadratu, to pamiętając że przekątna kwadratu dzieli nam kąt prosty na dwa kąty po \(45°\), otrzymamy następującą sytuację:



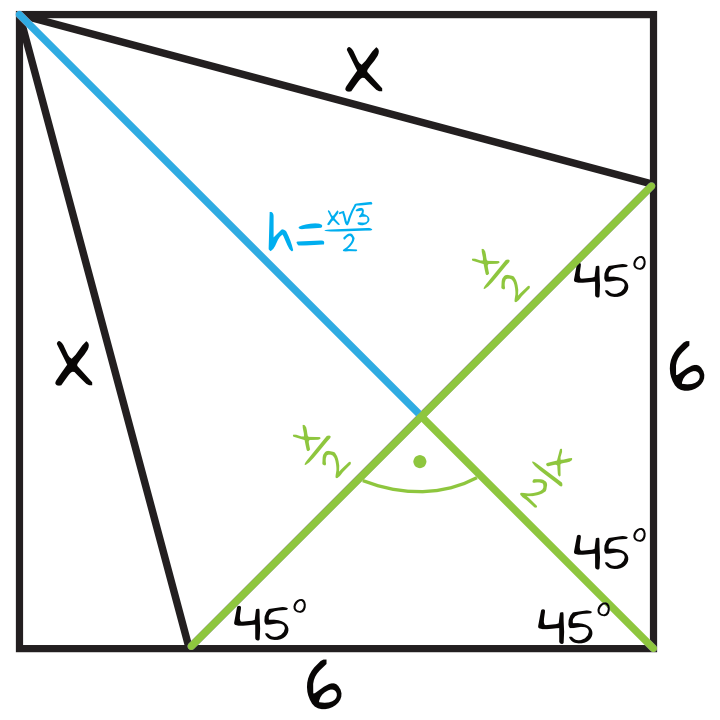
Krok 2. Zapisanie i rozwiązanie równania.
Kwadrat o boku \(6\) ma długość przekątnej równą \(6\sqrt{2}\). Patrząc się na rysunek widzimy, że ta przekątna składa się z wysokości trójkąta \(\frac{x\sqrt{3}}{2}\) oraz połowy boku trójkąta \(\frac{x}{2}\), zatem:
$$\frac{x\sqrt{3}}{2}+\frac{x}{2}=6\sqrt{2} \quad\bigg/\cdot2 \\
x\sqrt{3}+x=12\sqrt{2} \\
x(\sqrt{3}+1)=12\sqrt{2} \\
x=\frac{12\sqrt{2}}{\sqrt{3}+1} \\
x=\frac{12\sqrt{2}\cdot(\sqrt{3}-1)}{(\sqrt{3}+1)\cdot(\sqrt{3}-1)} \\
x=\frac{12\sqrt{2}\cdot(\sqrt{3}-1)}{3-1} \\
x=\frac{12\sqrt{2}\cdot(\sqrt{3}-1)}{2} \\
x=6\sqrt{2}\cdot(\sqrt{3}-1) \\
x=6\cdot(\sqrt{6}-\sqrt{2})$$

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz funkcję w postaci kanonicznej (patrz: Krok 2.).
2 pkt
• Gdy obliczysz wartość współczynnika \(a\) (patrz: Krok 3.).
3 pkt
• Gdy zapiszesz równanie w postaci \(f(x)=-3(x-2)^2+10\) (patrz: Krok 4.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.

Krok 1. Wyznaczenie współrzędnych wierzchołka paraboli.
Z treści zadania możemy odczytać bardzo ważną informację, a mianowicie współrzędne wierzchołka paraboli. Zastanówmy się co to znaczy, że funkcja rośnie w przedziale \((-\infty,2\rangle\) i że osiąga największą wartość równą \(10\). To by oznaczało, że nasza funkcja wygląda mniej więcej w ten sposób:



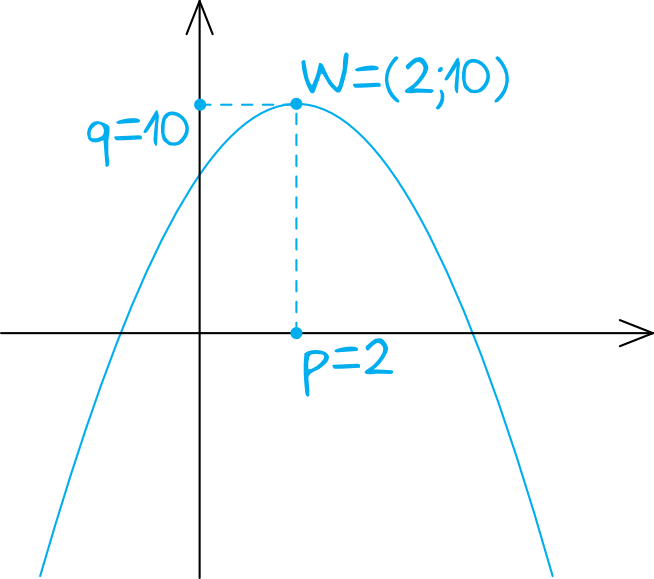
Wynika z tego, że funkcja ma wierzchołek w punkcie \(W=(2,10)\).

Krok 2. Zapisanie wzoru funkcji w postaci kanonicznej.
Znając współrzędne wierzchołka paraboli możemy zapisać ją w postaci kanonicznej:
$$f(x)=a(x-p)^2+q \\
f(x)=a(x-2)^2+10$$

Krok 3. Podstawienie współrzędnych punktu \(A\) oraz wyznaczenie współczynnika \(a\).
Do wyznaczonej przed chwilą postaci kanonicznej możemy podstawić współrzędne znanego nam punktu \(A\), co pozwoli wyznaczyć nam już jeden ze współczynników:
$$f(x)=a(x-2)^2+10 \\
-2=a(4-2)^2+10 \\
-2=a\cdot2^2+10 \\
-2=4a+10 \\
4a=-12 \\
a=-3$$

Krok 4. Wyznaczenie współczynników \(b\) oraz \(c\).
Znając współczynnik kierunkowy \(a=-3\) wiemy już, że w postaci kanonicznej nasza funkcja przyjmuje wzór:
$$f(x)=-3(x-2)^2+10$$

Jeżeli wykonamy teraz potęgowanie, to doprowadzimy funkcję do postaci ogólnej, co z kolei pozwoli nam odczytać wartości wszystkich współczynników:
$$f(x)=-3(x-2)^2+10 \\
f(x)=-3(x^2-4x+4)+10 \\
f(x)=-3x^2+12x-12+10 \\
f(x)=-3x^2+12x-2$$

To oznacza, że interesująca nas funkcja ma współczynniki:
$$a=-3,\;b=12,\;c=-2$$

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz, że drugi wyraz jest równy \(a_{1}+r\), czwarty wyraz jest równy \(a_{1}+3r\) oraz siódmy wyraz jest równy \(a_{1}+6r\).
2 pkt
• Gdy zapiszesz równanie typu \((4+r)^2+(4+3r)^2+(4+6r)^2=702\) (patrz: Krok 2.).
3 pkt
• Gdy doprowadzisz do równania kwadratowego w postaci ogólnej z której można potem liczyć deltę (patrz: Krok 2.).
4 pkt
• Gdy rozwiążesz powstałe równanie kwadratowe (patrz: Krok 3.).
5 pkt
• Gdy otrzymasz oczekiwany wynik.

Krok 1. Ułożenie układu równań.
Z treści zadania wynika, że możemy ułożyć następujący układ równań:
$$\begin{cases}
a_{1}=4 \\
{a_{2}}^2+{a_{4}}^2+{a_{7}}^2=702
\end{cases}$$

Aby rozwiązać ten układ równań musimy rozpisać wyrazy \(a_{2}\), \(a_{4}\) oraz \(a_{7}\) zgodnie ze wzorem na \(n\)-ty wyraz ciągu arytmetycznego \(a_{n}=a_{1}+(n-1)r\). W związku z tym otrzymamy:
$$\begin{cases}
a_{1}=4 \\
(a_{1}+r)^2+(a_{1}+3r)^2+(a_{1}+6r)^2=702
\end{cases}$$

Krok 2. Rozwiązanie układu równań.
Podstawiając \(a_{1}=4\) z pierwszego równania do drugiego otrzymamy:
$$(4+r)^2+(4+3r)^2+(4+6r)^2=702 \\
16+8r+r^2+16+24r+9r^2+16+48r+36r^2=702 \\
46r^2+80r+48=702 \\
46r^2+80r-654=0$$

Krok 3. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=46,\;b=80,\;c=-654\)
$$Δ=b^2-4ac=80^2-4\cdot46\cdot(-654)=6400-(-120336)=126736 \\
\sqrt{Δ}=\sqrt{126736}=356$$

$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-80-356}{2\cdot46}=\frac{-436}{92}=-\frac{109}{23} \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-80+356}{2\cdot46}=\frac{276}{92}=3$$

Żadnej z tych wartości odrzucić nie możemy (moglibyśmy odrzucić, gdyby np. podana była informacja o tym że ciąg jest rosnący). W związku z tym zostaje nam \(r_{1}=-\frac{109}{23}\) oraz \(r_{2}=3\).

Krok 4. Wyznaczenie wzoru ogólnego tego ciągu.
Aby wyznaczyć wzór ogólny ciągu wystarczy podstawić \(a_{1}\) oraz \(r\) do wzoru:
$$a_{n}=a_{1}+(n-1)r$$

Z racji tego iż mamy dwie możliwości podstawienia różnicy to otrzymamy dwa rozwiązania tego zadania:
Gdy \(r=-\frac{109}{23}\):
$$a_{n}=4+(n-1)\cdot\left(-\frac{109}{23}\right) \\
a_{n}=4+(-\frac{109}{23}n)+\frac{109}{23} \\
a_{n}=4-\frac{109}{23}n+\frac{109}{23} \\
a_{n}=\frac{92}{23}-\frac{109}{23}n+\frac{109}{23} \\
a_{n}=-\frac{109}{23}n+\frac{201}{23}$$

Gdy \(r=3\):
$$a_{n}=4+(n-1)\cdot3 \\
a_{n}=4+3n-3 \\
a_{n}=3n+1$$

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy sporządzisz rysunek pomocniczy wraz z oznaczeniami (patrz: Krok 1.).
2 pkt
• Gdy obliczysz długość krawędzi podstawy (patrz: Krok 3.).
ALBO
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 4.).
ALBO
• Gdy obliczysz wysokość ściany bocznej (patrz: Krok 5.).
3 pkt
• Gdy obliczysz dwie z tych trzech długości: krawędź podstawy (patrz: Krok 3.), wysokość ostrosłupa (patrz: Krok 4.), wysokość ściany bocznej (patrz: Krok 5.).
4 pkt
• Gdy obliczysz wszystkie kluczowe długości: krawędź podstawy (patrz: Krok 3.), wysokość ostrosłupa (patrz: Krok 4.), wysokość ściany bocznej (patrz: Krok 5.).
5 pkt
• Gdy obliczysz objętość ostrosłupa (patrz: Krok 6.).
6 pkt
• Gdy otrzymasz oczekiwany wynik.

Krok 1. Sporządzenie rysunku pomocniczego.
Nanieśmy na rysunek informacje z treści zadania.



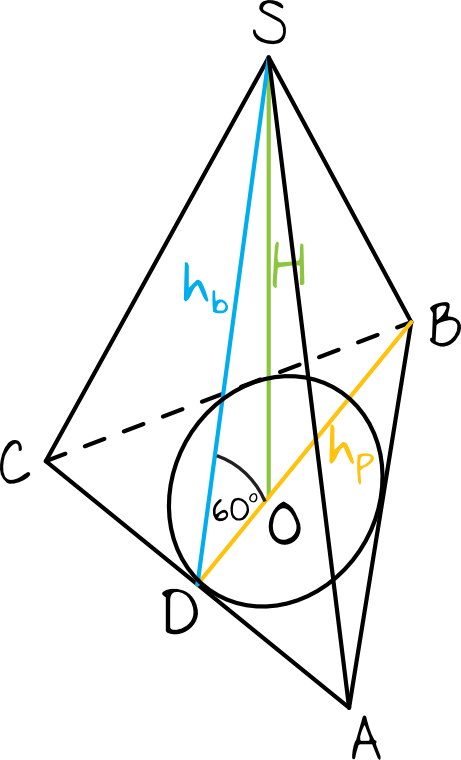
Krok 2. Obliczenie wysokości trójkąta znajdującego się w podstawie.
Z własności okręgów wpisanych w trójkąt równoboczny wiemy, że długość promienia okręgu jest równa \(\frac{1}{3}\) wysokości takiego trójkąta, zatem:
$$h_{p}=3\cdot6=18$$

Krok 3. Obliczenie długości boku trójkąta znajdującego się w podstawie.
W podstawie znajduje się trójkąt równoboczny o wysokości \(h_{p}=18\), zatem jego długość boku będzie równa:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
18=\frac{a\sqrt{3}}{2} \\
36=a\sqrt{3} \\
a=\frac{36}{\sqrt{3}} \\
a=\frac{36\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \\
a=\frac{36\sqrt{3}}{3} \\
a=12\sqrt{3}$$

Krok 4. Obliczenie wysokości ostrosłupa.
Spójrzmy na trójkąt \(SOD\). Wiemy, że podstawa tego trójkąta (czyli odcinek \(DO\) będący promieniem okręgu) ma długość \(r=6\). Korzystając z funkcji trygonometrycznych (a konkretnie z tangensa) możemy zapisać, że:
$$tg60°=\frac{H}{|DO|} \\
\sqrt{3}=\frac{H}{6} \\
H=6\sqrt{3}$$

Krok 5. Obliczenie wysokości ściany bocznej.
Ponownie spoglądamy na trójkąt \(SOD\). Do obliczenia pola powierzchni bocznej potrzebujemy znać długość wysokości ściany bocznej, a tę możemy obliczyć albo z Twierdzenia Pitagorasa (bo wiemy już, że przyprostokątne mają długości \(|DO|=6\) oraz \(H=6\sqrt{3}\)), albo po prostu z cosinusa:
$$cos60°=\frac{|DO|}{h_{b}} \\
\frac{1}{2}=\frac{6}{h_{b}} \\
\frac{1}{2}h_{b}=6 \\
h_{b}=12$$

Krok 6. Obliczenie objętości ostrosłupa.
Mamy już komplet informacji na temat naszego ostrosłupa, bo wiemy że \(a=12\sqrt{3}\) oraz \(H=6\sqrt{3}\), więc możemy przystąpić do obliczenia objętości, korzystając ze wzoru:
$$V=\frac{1}{3}\cdot P_{p}\cdot H \\
V=\frac{1}{3}\cdot\frac{a^2\sqrt{3}}{4}\cdot H \\
V=\frac{1}{3}\cdot\frac{(12\sqrt{3})^2\sqrt{3}}{4}\cdot6\sqrt{3} \\
V=\frac{1}{3}\cdot\frac{432\sqrt{3}}{4}\cdot6\sqrt{3} \\
V=\frac{1}{3}\cdot108\sqrt{3}\cdot6\sqrt{3} \\
V=36\sqrt{3}\cdot6\sqrt{3} \\
V=216\cdot3 \\
V=648$$

Krok 7. Obliczenie pola powierzchni bocznej.
W powierzchni bocznej mamy trzy trójkąty o podstawie \(a=12\sqrt{3}\) oraz wysokości \(h_{b}=12\), zatem:
$$P_{b}=3\cdot\frac{1}{2}\cdot a\cdot h_{b} \\
P_{b}=3\cdot\frac{1}{2}\cdot12\sqrt{3}\cdot12 \\
P_{b}=3\cdot6\sqrt{3}\cdot12 \\
P_{b}=216\sqrt{3}$$