Matura poprawkowa z matematyki (poziom podstawowy) - Sierpień 2018
Arkusz maturalny zawiera 25 zadań zamkniętych oraz 9 zadań otwartych. Łącznie do zdobycia jest 50 punktów, a sugerowany maksymalny czas rozwiązywania to 170 minut.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Cena pewnego towaru w wyniku obniżki o \(10\%\) zmniejszyła się o \(2018\) zł. Ten towar po tej obniżce kosztował:
Zadanie 2. (1pkt) Liczba \(\sqrt{\sqrt[3]{2}}\) jest równa:
Zadanie 3. (1pkt) Dane są liczby \(x=4,5\cdot10^{-8}\) oraz \(y=1,5\cdot10^{2}\). Wtedy iloraz \(\frac{x}{y}\) jest równy:
Zadanie 4. (1pkt) Liczba \(log_{4}96-log_{4}6\) jest równa:
Zadanie 5. (1pkt) Równość \((a+2\sqrt{3})^2=13+4\sqrt{3}\) jest prawdziwa dla:
Zadanie 6. (1pkt) Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi \(x\) i \(y\).
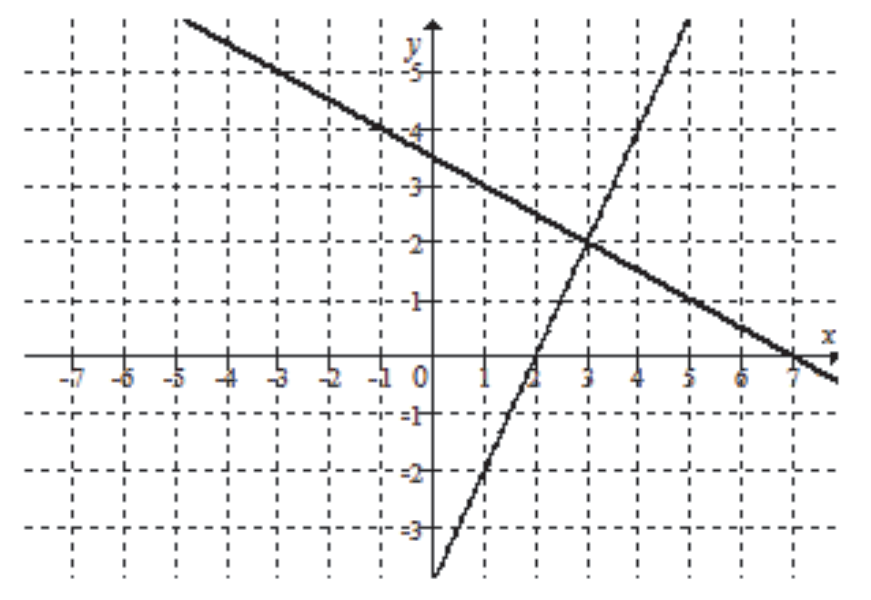
Wskaż ten układ.
Zadanie 7. (1pkt) Rozwiązaniem równania \(\frac{x-2}{3(x+2)}=\frac{1}{9}\) jest liczba:
Zadanie 8. (1pkt) Dane są funkcje \(f(x)=3^x\) oraz \(g(x)=f(-x)\), określone dla wszystkich liczb rzeczywistych \(x\). Punkt wspólny wykresów funkcji \(f\) i \(g\):
Zadanie 9. (1pkt) Punkt \((1,\sqrt{3})\) należy do wykresu funkcji \(y=2\sqrt{3}x+b\). Współczynnik \(b\) jest równy:
Zadanie 10. (1pkt) Wykresem funkcji kwadratowej \(f(x)=x^2-2x-11\) jest parabola, której wierzchołkiem jest punkt o współrzędnych:
Zadanie 11. (1pkt) Funkcja kwadratowa jest określona wzorem \(f(x)=-3(x-2)(x-9)\). Liczby \(x_{1}\), \(x_{2}\) są różnymi miejscami zerowymi funkcji \(f\). Zatem:
Zadanie 12. (1pkt) Największą wartością funkcji \(y=-(x-2)^2+4\) w przedziale \(\langle3,5\rangle\) jest:
Zadanie 13. (1pkt) Ciąg arytmetyczny \((a_{n})\), określony dla \(n\ge1\), spełnia warunek \(a_{3}+a_{4}+a_{5}=15\). Wtedy:
Zadanie 14. (1pkt) Dla pewnej liczby \(x\) ciąg \((x, x+4, 16)\) jest geometryczny. Liczba \(x\) jest równa:
Zadanie 15. (1pkt) W trójkącie prostokątnym przeciwprostokątna ma długość \(3\), a długość przyprostokątnej leżącej naprzeciwko kąta \(α\) jest równa \(\sqrt{3}\). Zatem:
Zadanie 16. (1pkt) Kąt \(α\) jest ostry i \(cosα=\frac{3}{5}\). Wtedy:
Zadanie 17. (1pkt) Dany jest okrąg o środku \(S\). Punkty \(K\), \(L\), \(M\) leżą na tym okręgu. Na łuku \(KL\) tego okręgu są oparte kąty \(KSL\) i \(KML\) (zobacz rysunek), których miary \(α\) i \(β\) spełniają warunek \(α+β=114°\).

Wynika stąd, że:
Zadanie 18. (1pkt) Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa \(80°\). Kąt rozwarty tego równoległoboku ma miarę:
Zadanie 19. (1pkt) Pole trójkąta o bokach długości \(4\) oraz \(9\) i kącie między nimi o mierze \(60°\) jest równe:
Zadanie 20. (1pkt) Proste o równaniach \(y=(3m-4)x+2\) oraz \(y=(12-m)x+3m\) są równoległe, gdy:
Zadanie 21. (1pkt) Punkt \(A=(-3,2)\) jest końcem odcinka \(AB\), a punkt \(M=(4,1)\) jest środkiem tego odcinka. Długość odcinka \(AB\) jest równa:
Zadanie 22. (1pkt) Jeżeli \(α\) oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to:
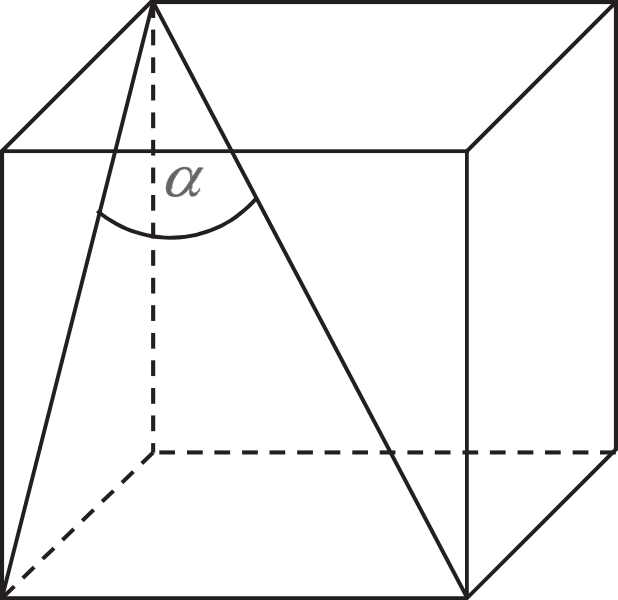
Zadanie 23. (1pkt) Przekrój osiowy walca jest kwadratem o przekątnej \(10\sqrt{2}\). Pole powierzchni bocznej tego walca jest równe:
Zadanie 24. (1pkt) Abiturient jednego z liceów zestawił w tabeli oceny ze swojego świadectwa ukończenia szkoły.

Mediana przedstawionego zestawu danych jest równa:
Zadanie 25. (1pkt) W grupie liczącej \(29\) uczniów (dziewcząt i chłopców) jest \(15\) chłopców. Z tej grupy trzeba wylosować jedną osobę. Prawdopodobieństwo zdarzenia polegającego na tym, że zostanie wylosowana dziewczyna, jest równe:
Zadanie 26. (2pkt) Rozwiąż nierówność \(x^2+6x-16\lt0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz miejsca zerowe, a w dalszej części zadania popełnisz błędy (patrz: Krok 1.).
ALBO
• Gdy błędnie wyznaczysz miejsca zerowe funkcji (np. w wyniku błędu rachunkowego przy liczeniu delty), ale dalszy tok rozwiązywania będzie poprawny.
2 pkt
• Gdy otrzymasz oczekiwany wynik (w postaci zapisanego przedziału lub w formie graficznej).
Wyjaśnienie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=1,\;b=6,\;c=-16\)
$$Δ=b^2-4ac=6^2-4\cdot1\cdot(-16)=36-(-64)=36+64=100 \\
\sqrt{Δ}=\sqrt{100}=10$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-6-10}{2\cdot1}=\frac{-16}{2}=-8 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-6+10}{2\cdot1}=\frac{4}{2}=2$$
Krok 2. Szkicowanie wykresu paraboli.
Współczynnik \(a\) jest dodatni, więc parabola ma ramiona skierowane do góry. Zaznaczamy na osi miejsca zerowe, które przed chwilą obliczyliśmy (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\lt\)) i szkicujemy wykres paraboli:

Krok 3. Odczytanie rozwiązania.
Interesuje nas przedział dla których zbiór argumentów przyjmuje wartość mniejszą od zera, czyli patrzymy na to co znalazło się pod osią. To oznacza, że rozwiązaniem tej nierówności jest przedział:
$$x\in(-8;2)$$
Zadanie 27. (2pkt) Rozwiąż równanie \((x^3+27)(x^2-16)=0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz dwa równania: \(x^3+27=0 \lor x^2-16=0\).
ALBO
• Gdy wskażesz poprawnie jedno lub dwa rozwiązania równania.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Równanie przedstawione jest w postaci iloczynowej, zatem aby całość była równa zero, to któryś z nawiasów musi dać nam wartość równą zero. W związku z tym:
$$(x^3+27)(x^2-16)=0 \\
x^3+27=0 \quad\lor\quad x^2-16=0 \\
x^3=-27 \quad\lor\quad x^2=16 \\
x=-3 \quad\lor\quad x=4 \quad\lor\quad x=-4$$
Zadanie 28. (2pkt) W równoległoboku \(ABCD\) punkt \(E\) jest środkiem boku \(BC\). Z wierzchołka \(D\) poprowadzono prostą przecinającą bok \(BC\) w punkcie \(E\). Proste \(AB\) i \(DE\) przecinają się w punkcie \(F\) (zobacz rysunek). Wykaż, że punkt \(B\) jest środkiem odcinka \(AF\).
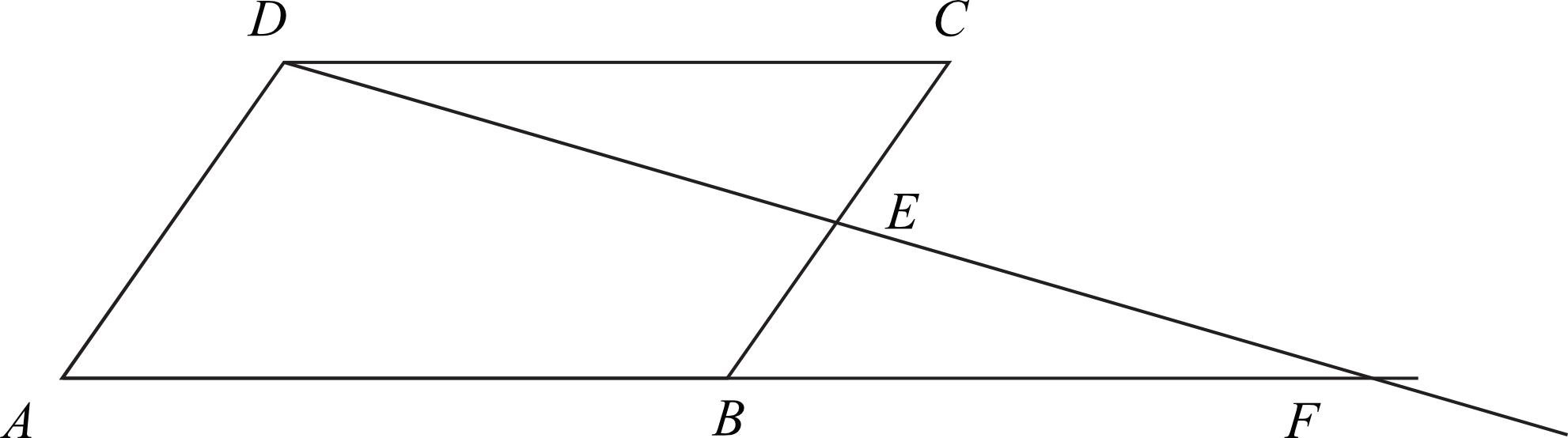
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy dostrzeżesz podobieństwo trójkątów \(BFE\) oraz \(AFD\) (patrz: Krok 2.).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Zgodnie z informacjami z treści zadania możemy oznaczyć sobie długości odcinków \(CE\) oraz \(EB\) jako \(x\), natomiast odcinek \(AD\) jako \(x+x=2x\). Dodatkowo oznaczmy też odcinek \(AB\) jako \(a\) oraz odcinek \(BF\) jako \(b\).
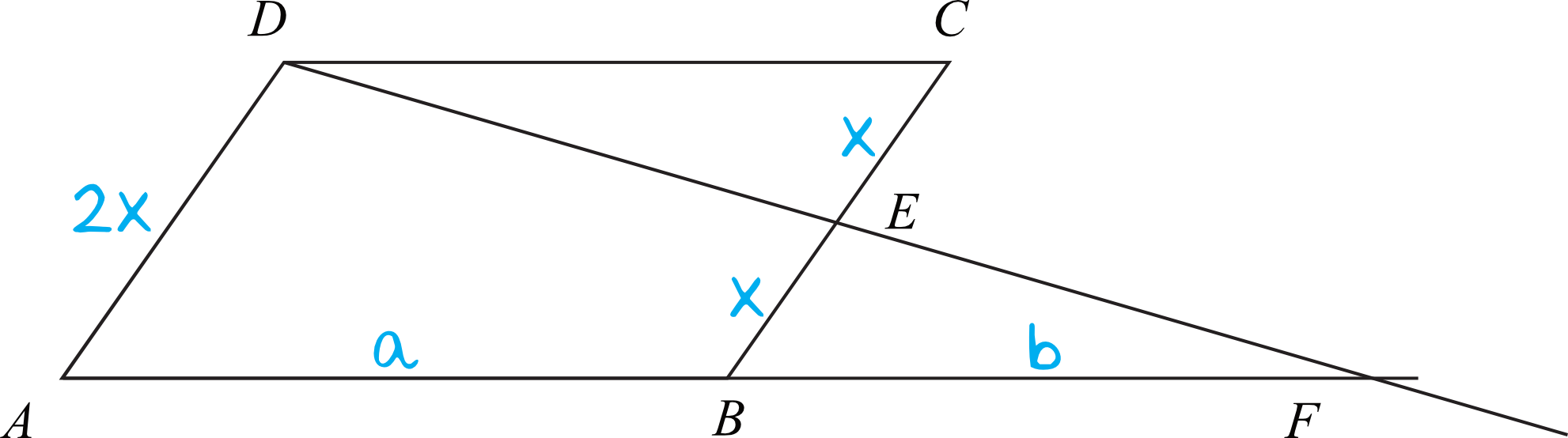
Krok 2. Dostrzeżenie podobieństwa trójkątów i zapisanie równania.
Trójkąty \(BFE\) oraz \(AFD\) są trójkątami podobnymi. Możemy być tego pewni, gdyż proste \(AD\) oraz \(BE\) są prostymi równoległymi (bo jest to równoległobok). Skoro tak, to możemy zapisać stosunki długości poszczególnych boków tworzą następujące równanie:
$$\frac{b}{x}=\frac{a+b}{2x}$$
Krok 3. Rozwiązanie powstałego równania.
Powstało nam równanie, które musimy teraz rozwiązać. Najprościej będzie zacząć od mnożenia na krzyż. Otrzymamy wtedy:
$$b\cdot2x=(a+b)\cdot x \\
2bx=ax+bx \quad\bigg/-bx \\
bx=ax \quad\bigg/:x \\
a=b$$
Krok 4. Zakończenie dowodzenia.
Udało nam się udowodnić, że odcinek \(a\) (czyli \(AB\)), jest równy odcinkowi \(b\) (czyli \(BF\)). To oznacza, że punkt \(B\) jest środkiem odcinka \(AF\), bo tylko środek odcinka może podzielić go na dwie równe części. Dowodzenie możemy uznać więc za skończone.
Zadanie 29. (2pkt) Wykaż, że jeżeli \(a\) i \(b\) są liczbami rzeczywistymi dodatnimi, to \((a+b)(\frac{1}{a}+\frac{1}{b})\ge4\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy otrzymasz pożądaną postać \((a-b)^2\ge0\), ale nie uzasadnisz dlaczego ta nierówność jest prawdziwa.
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Skoro \(a\) oraz \(b\) są liczbami dodatnimi, to możemy być pewni że dzieląc lub mnożąc obie strony nierówności przez te niewiadome nie będziemy musieli zmieniać znaku nierówności na przeciwny. W związku z tym możemy zacząć przekształcać naszą nierówność. Najlepiej będzie zacząć od wymnożenia wartości w nawiasach:
$$(a+b)\left(\frac{1}{a}+\frac{1}{b}\right)\ge4 \\
1+\frac{a}{b}+\frac{b}{a}+1\ge4 \\
\frac{a}{b}+\frac{b}{a}\ge2 \quad\bigg/\cdot b \\
a+\frac{b^2}{a}\ge2b \quad\bigg/\cdot a \\
a^2+b^2\ge2ab \\
a^2-2ab+b^2\ge0 \\
(a-b)^2\ge0$$
Z racji tego, iż każda liczba rzeczywista podniesiona do kwadratu daje wynik dodatni, to dowodzenie możemy uznać za zakończone.
Zadanie 30. (2pkt) Dziewiąty wyraz ciągu arytmetycznego \((a_{n})\), określonego dla \(n\ge1\), jest równy \(34\), a suma jego ośmiu początkowych wyrazów jest równa \(110\). Oblicz pierwszy wyraz i różnicę tego ciągu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy ułożysz układ równań składający się z równań typu \(a_{1}+8r=34\) oraz \(2a_{1}+7r=27,5\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Ułożenie układu równań
Korzystając ze wzoru ogólnego na \(n\)-ty wyraz ciągu arytmetycznego \(a_{n}=a_{1}+(n-1)r\) możemy zapisać, że:
$$a_{9}=a_{1}+8r \\
a_{1}+8r=34$$
To będzie nasze pierwsze równanie z którego zbudujemy układ równań. Drugie równanie będzie wynikać z informacji na temat sumy ośmiu początkowych wyrazów:
$$S_{n}=\frac{a_{1}+a_{n}}{2}\cdot n \\
S_{8}=\frac{a_{1}+a_{8}}{2}\cdot8 \\
110=\frac{a_{1}+a_{8}}{2}\cdot8 \\
110=(a_{1}+a_{8})\cdot4 \quad\bigg/:4 \\
a_{1}+a_{8}=27,5 \\
a_{1}+a_{1}+7r=27,5 \\
2a_{1}+7r=27,5$$
To oznacza, że możemy stworzyć następujący układ równań:
$$\begin{cases}
a_{1}+8r=34 \\
2a_{1}+7r=27,5
\end{cases}$$
Krok 2. Rozwiązanie powstałego układu równań i wyznaczenie różnicy ciągu arytmetycznego.
Najprościej będzie zastosować tutaj metodę podstawiania, wyznaczając wartość \(a_{1}\) z pierwszego równania:
$$\begin{cases}
a_{1}=34-8r \\
2a_{1}+7r=27,5
\end{cases}$$
Podstawiając teraz pierwsze równanie do drugiego otrzymamy:
$$2\cdot(34-8r)+7r=27,5 \\
68-16r+7r=27,5 \\
68-9r=27,5 \\
-9r=-40,5 \\
r=4,5$$
Krok 3. Obliczenie wartości pierwszego wyrazu.
Znając wartość \(r=4,5\) możemy obliczyć wartość pierwszego wyrazu, podstawiając wyliczoną różnicę do jednego z wyznaczonych równań:
$$a_{1}=34-8r \\
a_{1}=34-8\cdot4,5 \\
a_{1}=34-36 \\
a_{1}=-2$$
To oznacza, że \(a_{1}=-2\) oraz \(r=4,5\).
Zadanie 31. (2pkt) Punkty \(A=(2,4)\), \(B=(0,0)\), \(C=(4,-2)\) są wierzchołkami trójkąta \(ABC\). Punkt \(D\) jest środkiem boku \(AC\) tego trójkąta. Wyznacz równanie prostej \(BD\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz współrzędne punktu \(D\) (patrz: Krok 2.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować układ współrzędnych na którym zaznaczymy znane nam punkty i na którym poprowadzimy prostą \(BD\), której równania szukamy:
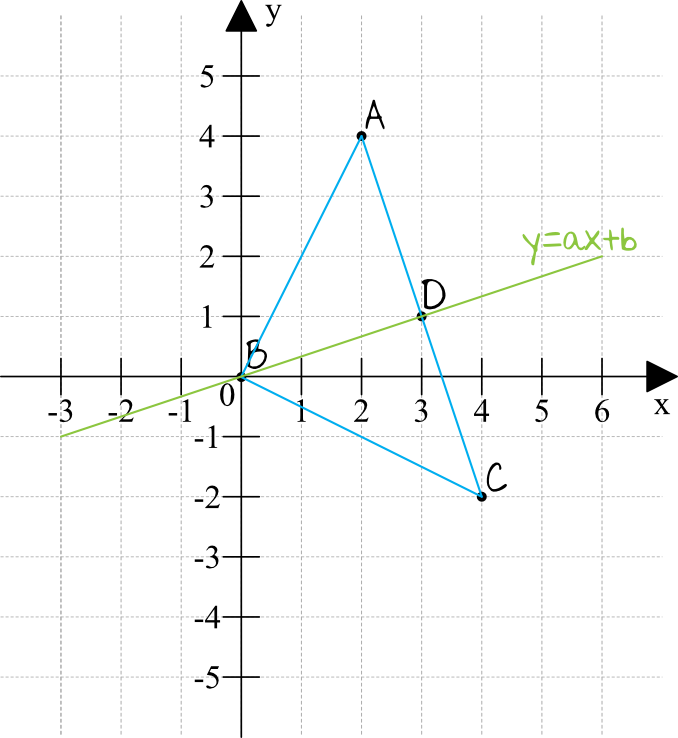
Krok 2. Obliczenie współrzędnych punktu \(D\).
Punkt \(D\) jest środkiem odcinka \(AC\). Znając współrzędne punktu \(A\) oraz \(C\) możemy bez przeszkód wyznaczyć współrzędne punktu \(D\), korzystając ze wzoru:
$$D=\left(\frac{x_{A}+x_{C}}{2};\frac{y_{A}+y_{C}}{2}\right)$$
Dla przejrzystości obliczeń wyznaczny każdą ze współrzędnych oddzielnie:
$$x_{D}=\frac{x_{A}+x_{C}}{2} \\
x_{D}=\frac{2+4}{2} \\
x_{D}=\frac{6}{2} \\
x_{D}=3 \\
\quad \\
y_{D}=\frac{y_{A}+y_{C}}{2} \\
y_{D}=\frac{4+(-2)}{2} \\
y_{D}=\frac{4-2}{2} \\
y_{D}=\frac{2}{2} \\
y_{D}=1$$
To oznacza, że \(D=(3;1)\).
Krok 3. Wyznaczenie równania prostej \(BD\).
Skoro znamy współrzędne punktów \(B\) oraz \(D\) to możemy teraz wyznaczyć równanie prostej przechodzącej przez te dwa punkty. Możemy to zrobić budując układ równań (podstawiając współrzędne punktu \(B\) oraz \(D\) do postaci \(y=ax+b\) uzyskamy dwa równania tworzące układ równań), albo też możemy skorzystać ze wzoru dostępnego w tablicach, czyli:
$$(y-y_{B})(x_{D}-x_{B})-(y_{D}-y_{B})(x-x_{B})=0$$
Metoda z układem równań wydaje się być w tym przypadku znacznie szybsza, zatem:
$$\begin{cases}
0=0+b \\
1=3a+b \\
\end{cases}$$
$$\begin{cases}
b=0 \\
1=3a+b
\end{cases}$$
Już z pierwszego równania wyszło nam samoistnie, że \(b=0\), co jest dobrą informacją, bo przecież współczynnik \(b\) informuje nas o miejscu przecięcia się prostej z osią igreków, a u nas prosta przechodzi przez początek układu współrzędnych. Znamy więc już wartość współczynnika \(b\), teraz musimy wyznaczyć współczynnik \(a\). Zrobimy to podstawiając po prostu \(b=0\) do drugiego równania:
$$1=3a+b \\
1=3a+0 \\
a=\frac{1}{3}$$
W związku z tym prosta \(BD\) wyraża się wzorem \(y=\frac{1}{3}x+0\), czyli po prostu \(y=\frac{1}{3}x\).
Zadanie 32. (5pkt) W ostrosłupie prawidłowym trójkątnym \(ABCS\) krawędź podstawy ma długość \(a\). Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.
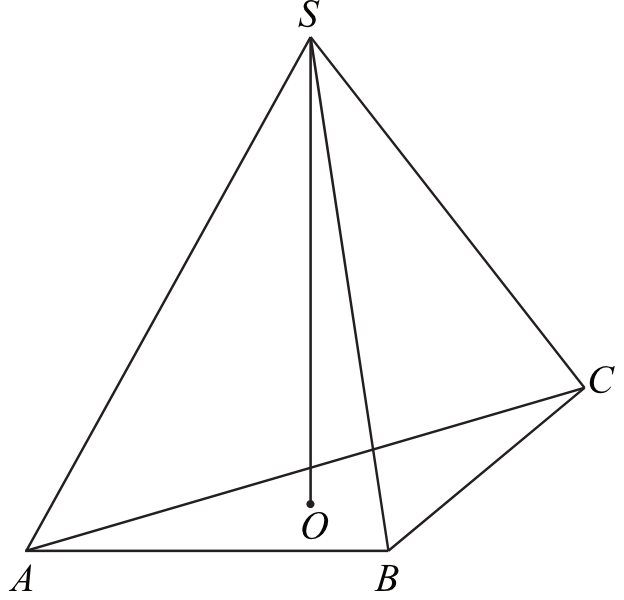
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy sporządzisz rysunek pomocniczy i zapiszesz, że \(cosα=\frac{|OC|}{|SC|}\).
2 pkt
• Gdy obliczysz długość odcinka \(OC\) (patrz: Krok 2.).
ALBO
• Gdy obliczysz długość odcinka \(DS\) (patrz: Krok 3.).
3 pkt
• Gdy długość odcinka \(OC\) (patrz: Krok 2.) oraz \(DS\) (patrz: Krok 3.).
4 pkt
• Gdy obliczysz długość odcinka \(SC\) (patrz: Krok 4.).
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy sobie nasz ostrosłup i wprowadźmy proste oznaczenia, pamiętając o tym że skoro jest to ostrosłup prawidłowy trójkątny, to w podstawie musi znaleźć się trójkąt równoboczny:
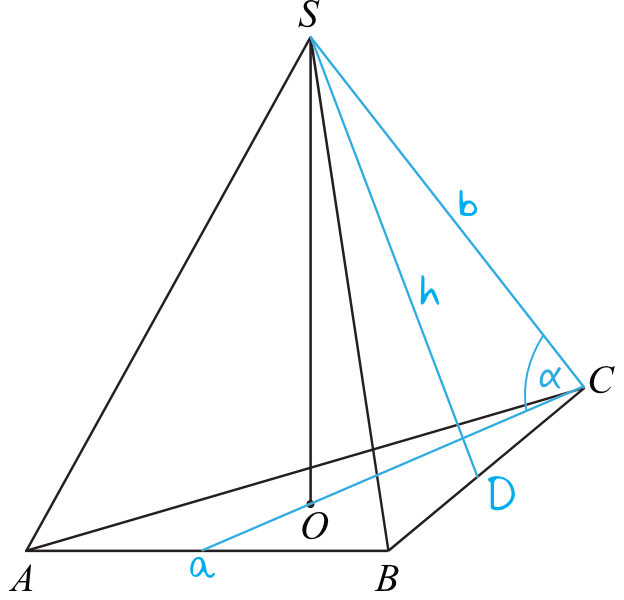
Musimy obliczyć cosinus kąta \(α\), czyli:
$$cosα=\frac{|OC|}{|SC|}$$
To oznacza, że będziemy chcieli poznać długości odcinków \(OC\) oraz \(SC\). Długości jako takich na pewno nie poznamy, bo w zadaniu nie występują konkretne liczby, dlatego będziemy musieli operować na wyrażeniach algebraicznych i powiązaniach poszczególnych długości z długością \(a\). Na tym tak naprawdę polegać będzie cała trudność tego zadania.
Krok 2. Obliczenie długości odcinka \(OC\).
Odcinek \(OC\) stanowi \(\frac{2}{3}\) długości wysokości trójkąta równobocznego znajdującego się w podstawie (wynika to z własności ostrosłupów prawidłowych trójkątnych). Korzystając ze wzoru na wysokość trójkąta równobocznego możemy zapisać, że:
$$|OC|=\frac{2}{3}\cdot h \\
|OC|=\frac{2}{3}\cdot\frac{a\sqrt{3}}{2} \\
|OC|=\frac{2}{3}\cdot\frac{a\sqrt{3}}{2} \\
|OC|=\frac{2a\sqrt{3}}{6} \\
|OC|=\frac{a\sqrt{3}}{3}$$
Krok 3. Obliczenie długości odcinka \(DS\).
Odcinek \(DS\) (wysokość ściany bocznej oznaczona jako \(h\)) przyda nam się do obliczenia długości krawędzi bocznej, czyli boku \(SC\). Z treści zadania wynika, że pole powierzchni bocznej jest dwa razy większe od pola podstawy. W związku z tym:
$$P_{b}=2P_{p} \\
P_{b}=2\cdot\frac{a^2\sqrt{3}}{4} \\
P_{b}=\frac{a^2\sqrt{3}}{2}$$
Pole powierzchni bocznej to pole trzech trójkątów równoramiennych, każdy o boku \(a\) oraz wysokości \(h\), zatem:
$$P_{b}=3\cdot\frac{1}{2}\cdot a\cdot h \\
P_{b}=\frac{3}{2}\cdot a\cdot h$$
Przyrównując teraz do siebie te dwa wyznaczone równania otrzymamy:
$$\frac{3}{2}\cdot a\cdot h=\frac{a^2\sqrt{3}}{2} \quad\bigg/\cdot2 \\
3a\cdot h=a^2\sqrt{3} \quad\bigg/:3a \\
h=\frac{a^2\sqrt{3}}{3a} \\
h=\frac{a\sqrt{3}}{3}$$
W związku z tym: \(|DS|=\frac{a\sqrt{3}}{3}\).
Krok 4. Obliczenie długości odcinka \(SC\).
Spójrzmy na trójkąt \(DCS\). Długość kluczowego odcinka \(SC\) (oznaczonego na rysunku jako \(b\)) obliczymy korzystając z Twierdzenia Pitagorasa. Odcinek \(DC\) będący dolną przyprostokątną tego trójkąta ma długość \(\frac{1}{2}a\) (bo wysokość w trójkącie równobocznym dzieli podstawę na dwie równe części). Odcinek \(DS\) który jest drugą przyprostokątną wyliczyliśmy przed chwilą i wiemy że \(DS=\frac{a\sqrt{3}}{3}\), zatem:
$$|DC|^2+|DS|^2=|SC|^2 \\
\left(\frac{1}{2}a\right)^2+\left(\frac{a\sqrt{3}}{3}\right)^2=b^2 \\
\frac{1}{4}a^2+\frac{a^2\cdot3}{9}=b^2 \\
\frac{a^2}{4}+\frac{a^2}{3}=b^2 \\
\frac{3a^2}{12}+\frac{4a^2}{12}=b^2 \\
\frac{7a^2}{12}=b^2 \\
b=\sqrt{\frac{7a^2}{12}} \\
b=\frac{\sqrt{7a^2}}{\sqrt{12}} \\
b=\frac{\sqrt{7}a}{\sqrt{4\cdot3}} \\
b=\frac{\sqrt{7}a}{2\sqrt{3}} \\
b=\frac{\sqrt{7}a\cdot\sqrt{3}}{2\sqrt{3}\cdot\sqrt{3}} \\
b=\frac{\sqrt{21}a}{2\cdot3} \\
b=\frac{\sqrt{21}a}{6}$$
To oznacza, że krawędź boczna ma długość \(|SC|=\frac{\sqrt{21}a}{6}\).
Krok 5. Obliczenie wartości \(cosα\).
Mamy już wszystkie potrzebne dane, zatem możemy zapisać, że:
$$cosα=\frac{|OC|}{|SC|} \\
cosα=\frac{\frac{a\sqrt{3}}{3}}{\frac{\sqrt{21}a}{6}} \\
cosα=\frac{a\sqrt{3}}{3}:\frac{\sqrt{21}a}{6} \\
cosα=\frac{a\sqrt{3}}{3}\cdot\frac{6}{\sqrt{21}a} \\
cosα=\frac{6a\sqrt{3}}{3\sqrt{21}a} \\
cosα=\frac{2a\sqrt{3}}{\sqrt{21}a} \\
cosα=\frac{2a\sqrt{3}}{\sqrt{7}\cdot\sqrt{3}\cdot a} \\
cosα=\frac{2}{\sqrt{7}} \\
cosα=\frac{2\cdot\sqrt{7}}{\sqrt{7}\cdot\sqrt{7}} \\
cosα=\frac{2\sqrt{7}}{7}$$
Zadanie 33. (4pkt) Ze zbioru \(A=\{-3, -2, -1, 1, 2, 3\}\) losujemy liczbę \(a\), natomiast ze zbioru \(B=\{-1, 0, 1, 2\}\) losujemy liczbę \(b\). Te liczby są odpowiednio współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej \(f(x)=ax+b\). Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja \(f\) jest rosnąca i ma dodatnie miejsce zerowe.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
ALBO
• Gdy wykonasz wszystkie kroki, ale otrzymasz wynik większy od \(1\).
1 pkt
• Gdy obliczysz liczbę zdarzeń elementarnych \(|Ω|=24\) (patrz: Krok 1.).
ALBO
• Gdy zapiszesz, że aby funkcja była rosnąca, to współczynnik kierunkowy \(a\) musi być dodatni, czyli że ze zbioru \(A\) interesują nas liczby \(1,2,3\) (patrz: Krok 2.).
ALBO
• Gdy zapiszesz, że ze zbioru \(B\) interesuje nas jedynie wartość \(-1\) (patrz: Krok 2.).
2 pkt
• Gdy obliczysz liczbę zdarzeń elementarnych \(|Ω|=24\) (patrz: Krok 1.) oraz zapiszesz jakie liczby nas interesują ze zbioru \(A\) lub \(B\) (patrz: Krok 2.).
ALBO
• Gdy zapiszesz jakie liczby interesują nas ze zbioru \(A\) oraz \(B\) (patrz: Krok 2.).
3 pkt
• Gdy obliczysz liczbę zdarzeń elementarnych \(|Ω|=24\) (patrz: Krok 1.) oraz liczbę zdarzeń sprzyjających \(|A|=3\) (patrz: Krok 2.), ale nie obliczysz prawdopodobieństwa.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
To zadanie rozwiążemy sobie na dwa sposoby, ponieważ istnieje tutaj bardzo szybka droga do poznania prawidłowej odpowiedzi.
I sposób - obliczając liczbę zdarzeń elementarnych i sprzyjających.
Krok 1. Obliczenie liczby wszystkich zdarzeń elementarnych.
Z pierwszego zbioru możemy wylosować jedną z sześciu liczb. Z drugiego zbioru możemy wylosować jedną z czterech liczb. W związku zgodnie z regułą mnożenia wszystkich zdarzeń elementarnych będziemy mieć:
$$|Ω|=6\cdot4=24$$
Krok 2. Obliczenie liczby zdarzeń sprzyjających.
Musimy teraz ustalić jaka para liczb będzie tworzyć zdarzenie sprzyjające, zatem musimy ustalić które liczby ze zbioru \(A\) oraz \(B\) pasują nam do warunków zadania. Aby funkcja była rosnąca, to współczynnik kierunkowy \(a\) musi być dodatni. To oznacza, że z pierwszego zbioru interesują nas tylko liczby \(1,2,3\).
Teraz musimy ustalić jakie liczby interesują nas ze zbioru \(B\), a wpływ na to mieć będzie informacja mówiąca o tym, iż funkcja ma mieć dodatnie miejsca zerowe. Co to oznacza, że miejsca zerowe są dodatnie? Jeżeli funkcja przecina oś iksów dla np. \(x=-2\), to znaczy że miejsce zerowe jest ujemne (taki przypadek nas nie interesuje). Jeżeli funkcja przecina oś iksów dla np. \(x=3\) to wtedy miejsce zerowe jest dodatnie. Jak więc ustalić kiedy funkcja osiąga dodatnie miejsce zerowe?
Aby funkcja liniowa (która jest rosnąca) miała dodatnie miejsce zerowe dodatnie, to musi przecinać oś igreków w ujemnej wartości (czyli pod osią iksów), nie ma innej możliwości. O miejscu przecięcia się z osią igreków informuje nas współczynnik \(b\) i już po tej prostej analizie wiemy, że musi on być ujemny. To by oznaczało, że ze zbioru \(B\) interesowałaby nas jedynie wartość \(-1\).
Jeżeli jednak nie dostrzegliśmy tej własności, to możemy podejść do zagadnienia z innej strony. Aby wyznaczyć miejsce zerowe funkcji (jakiekolwiek) to musimy przyrównać wzór funkcji do zera. Zatem:
$$ax+b=0 \\
ax=-b \\
x=\frac{-b}{a}$$
My musimy mieć to miejsce zerowe większe od zera, czyli interesuje nas sytuacja w której:
$$\frac{-b}{a}\gt0$$
Skoro w naszym przypadku \(a\) jest dodatnie, to aby wyrażenie \(\frac{-b}{a}\) było większe od zera, to w liczniku musimy mieć także liczbę dodatnią. To oznacza, że \(b\) musi być liczbą ujemną. Z podanych liczb w zbiorze \(B\) tylko liczba \(-1\) spełnia ten warunek.
Skoro więc ze zbioru \(A\) interesują nas liczby \(1,2,3\), a ze zbioru \(B\) interesuje nas jedynie \(-1\), to zdarzeniami sprzyjającymi będą:
$$(1;-1), (2;-1), (3;-1)$$
Są to więc tylko trzy pary liczb, zatem \(|A|=3\).
Krok 3. Obliczenie prawdopodobieństwa.
$$P(A)=\frac{|A|}{|Ω|}=\frac{3}{24}=\frac{1}{8}$$
II sposób - dostrzegając własności wykresu funkcji liniowej.
Moglibyśmy dostrzec, że aby funkcja była rosnąca i miała dodatnie miejsce zerowe, musi ona wyglądać mniej więcej w ten sposób:
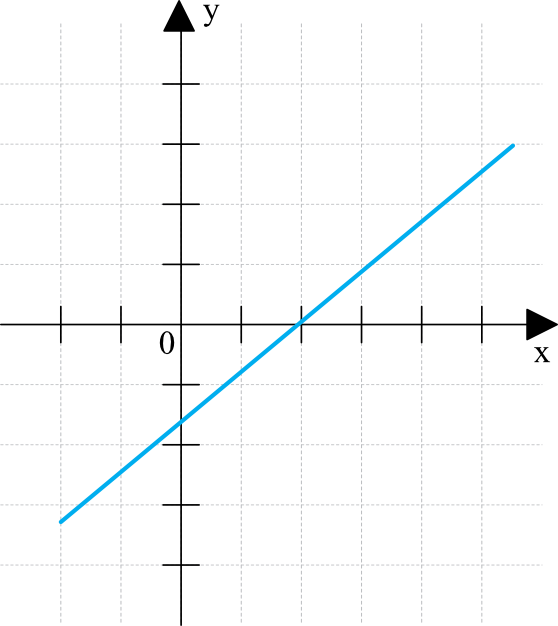
Funkcja ma być rosnąca, czyli współczynnik \(a\) musi być dodatni. Z sześciu podanych liczb tylko trzy są dodatnie, więc prawdopodobieństwo wylosowania dodatniego współczynnika \(a\) jest równe \(\frac{1}{2}\). Z analizy wykresu wynika też, że współczynnik \(b\) musi być ujemny, bo prosta przetnie nam oś \(OY\) dla ujemnej wartości \(y\). Tylko jedna z czterech proponowanych liczb jest ujemna, więc szanse wylosowania ujemnej liczby wyniosą \(\frac{1}{4}\). Prawdopodobieństwo wylosowania więc jednocześnie odpowiedniej liczby \(a\) oraz \(b\) będzie równe iloczynowi wyznaczonych przed chwilą prawdopodobieństw:
$$p=\frac{1}{2}\cdot\frac{1}{4}=\frac{1}{8}$$
Zadanie 34. (4pkt) W trójkącie prostokątnym \(ACB\) przyprostokątna \(AC\) ma długość \(5\), a promień okręgu wpisanego w ten trójkąt jest równy \(2\). Oblicz pole trójkąta \(ACB\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy sporządzisz rysunek pomocniczy korzystając z własności stycznych do okręgu (patrz: Krok 1.).
2 pkt
• Gdy zapiszesz równanie typu \((2+x)^2+5^2=(3+x)^2\) korzystając z Twierdzenia Pitagorasa (patrz: Krok 2.).
3 pkt
• Gdy obliczysz długość boku \(AB\) (patrz: Krok 3.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Boki trójkąta są tak naprawdę stycznymi do okręgu, zatem wykorzystując własności stycznych do okręgu możemy stworzyć taki oto rysunek pomocniczy:
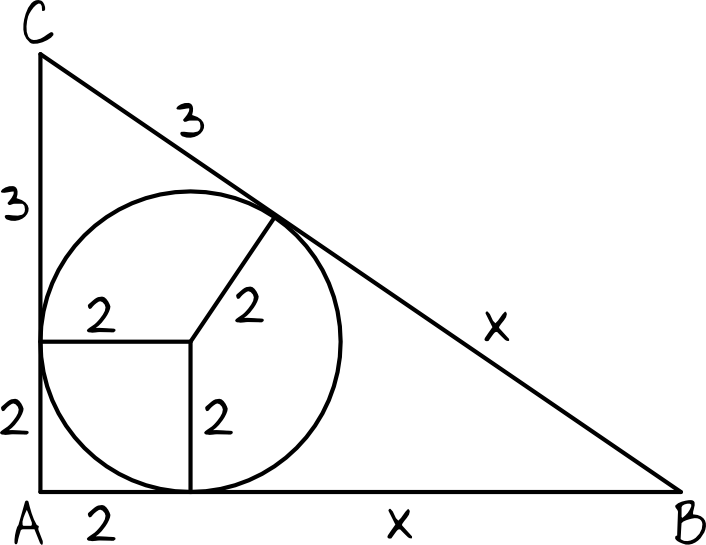
Krok 2. Obliczenie wartości niewiadomej \(x\).
Skoro jest to trójkąt prostokątny, to możemy skorzystać z Twierdzenia Pitagorasa:
$$|AB|^2+|AC|^2=|BC|^2 \\
(2+x)^2+5^2=(3+x)^2 \\
4+4x+x^2+25=9+6x+x^2 \quad\bigg/-x^2 \\
4+4x+25=9+6x \\
4x+29=9+6x \\
-2x+29=9 \\
-2x=-20 \\
x=10$$
Krok 3. Obliczenie długości boku \(AB\).
Skoro \(x=10\), to znaczy że:
$$|AB|=2+x \\
|AB|=2+10 \\
|AB|=12$$
Krok 4. Obliczenie pola powierzchni trójkąta.
Wiemy już, że podstawa trójkąta ma długość \(12\) i wysokość \(5\), zatem:
$$P=\frac{1}{2}ah \\
P=\frac{1}{2}\cdot12\cdot5 \\
P=6\cdot5 \\
P=30$$