Próbny egzamin ósmoklasisty z matematyki - Operon 2021
Arkusz zawiera 15 zadań zamkniętych oraz 4 zadania otwarte. Łącznie do zdobycia jest 25 punktów, a sugerowany maksymalny czas rozwiązywania to około 100 minut.
Zadanie 1. (1pkt) Dane są cztery różne liczby:
$$\frac{2}{3};\quad 0,06;\quad \frac{11}{9};\quad 0,(5)$$
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F, jeśli jest fałszywe.
Każda z liczb jest ułamkiem właściwym.
Wartość każdej z liczb jest większa niż \(\frac{1}{2}\).
Zadanie 2. (1pkt) Wartością wyrażenia \(-1\frac{1}{2}+2\frac{1}{4}:(-0,5)\) jest liczba:
Zadanie 3. (1pkt) Kwotę \(187 zł\) podzielono na dwie części w ten sposób, że jedna część była o \(20\%\) większa od drugiej. Otrzymana w ten sposób większa część kwoty to:
Zadanie 4. (1pkt) Rozwiązaniem równania \(\dfrac{x+2}{3}=\dfrac{5}{6}\) jest liczba:
Zadanie 5. (1pkt) Basia ma dwie siostry. Wszystkie trzy dziewczęta mają łącznie \(45\) lat. Basia ma \(14\) lat, a różnica wieku między najstarszą a najmłodszą z sióstr wynosi \(5\) lat.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F, jeśli jest fałszywe.
Basia jest najmłodszą z sióstr.
Średnia wieku wszystkich trzech sióstr wynosi \(15\) lat.
Zadanie 6. (1pkt) Sumę czterech kolejnych parzystych liczb podzielnych przez \(3\) zapisano w postaci iloczynu \(2^2\cdot3^3\). Największą z tych liczb jest liczba:
Zadanie 7. (1pkt) Wartość wyrażenia \(-4+3\cdot(-2)\) pomniejszona o liczbę \((-5)\) to:
Zadanie 8. (1pkt) Na uszycie \(15\) spódnic potrzeba \(21 m\) materiału.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Na uszycie trzech spódnic \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\) materiału.
Z \(33 m\) materiału można uszyć co najwyżej \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\) spódnice.
Zadanie 9. (1pkt) Andrzej ustalił, że w czasie jazdy rowerem w ciągu każdej minuty pokonuje średnio \(650 m\). Czy Andrzej przejedzie w kwadrans \(10 km\), jeśli będzie jechał z taką prędkością?
Wybierz odpowiedź A lub B i jej uzasadnienie spośród 1., 2. lub 3.
Zadanie 10. (1pkt) Pani Ela ma w portfelu dwa banknoty pięćdziesięciozłotowe, jeden dwudziestozłotowy i trzy dziesięciozłotowe. Za zakupy w sklepie ma zapłacić kwotę \(18,50 zł\). Prawdopodobieństwo, że pani Ela za te zakupy zapłaci jednym banknotem wynosi:
Zadanie 11. (1pkt) Z równoległoboku o krótszym boku długości \(6\) i kącie ostrym \(60°\) wycięto prostokąt o wymiarach największych z możliwych. Długość wyciętego w ten sposób prostokąta była dwa razy większa niż jego szerokość.

Drugi z boków danego równoległoboku miał długość:
Zadanie 12. (1pkt) Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Po uproszczeniu wyrażenia \(a^4\cdot a^3:a^2\) otrzymamy \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\).
Po uproszczeniu wyrażenia \((a^2 b)^3\cdot b\) otrzymamy \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\).
Zadanie 13. (1pkt) Dany jest prostokąt, którego szerokość ma o \(2 cm\) mniej od jego długości, a jego obwód wynosi \(28 cm\).
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Przekątna tego prostokąta ma długość \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\).
Szerokość prostokąta stanowi \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\) jego długości.
Zadanie 14. (1pkt) Na boku kwadratu \(ABCD\) zbudowano trójkąt równoboczny \(BEC\), jak na rysunku.
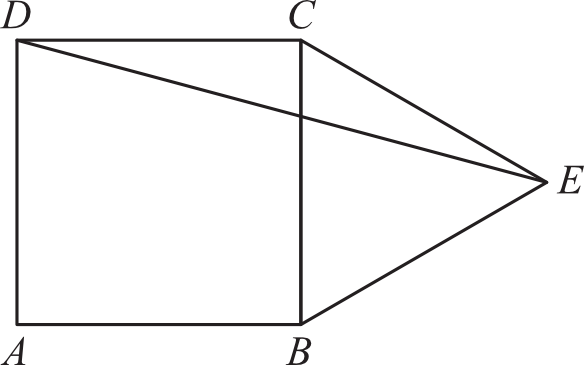
Kąt \(CDE\) ma miarę:
Zadanie 15. (1pkt) Komoda składająca się z dwóch szafek i trzech takich samych szuflad, każda o długości \(80 cm\), ma wymiary takie, jak pokazano na rysunku.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F, jeśli jest fałszywe.
Całkowita pojemność komody jest większa niż \(0,5 m^3\).
Pojemność jednej szuflady wynosi \(0,08 m3\).
Zadanie 16. (2pkt) Uzasadnij, że istnieje tylko jeden ułamek o mianowniku \(10\), który jest większy niż \(\frac{2}{3}\) i mniejszy niż \(\frac{4}{5}\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Do zadania można podejść na różne sposoby. Moglibyśmy zauważyć, że \(\frac{2}{3}=0,(6)\) i że \(\frac{4}{5}=0,8\). Jedynym ułamkiem o mianowniku \(10\), który jest pomiędzy tymi liczbami będzie ułamek \(\frac{7}{10}\), co zakończyłoby nasze dowodzenie.
Ewentualnie, dobrym pomysłem byłoby też rozszerzenie wszystkich ułamków w taki sposób, by w mianowniku ułamków znalazł się mianownik równy \(30\). Dlaczego \(30\)? Ponieważ jest to NWW liczb \(3\), \(5\) oraz \(10\). Zatem:
$$\frac{2}{3}=\frac{20}{30} \\
\frac{4}{5}=\frac{24}{30}$$
Istnieje tylko jeden ułamek zwykły, który jest większy od \(\frac{20}{30}\) i mniejszy od \(\frac{24}{30}\), który jest jednocześnie skracalny do ułamka o mianowniku \(10\) i tym ułamkiem jest \(\frac{21}{30}\), który skróci się do postaci \(\frac{7}{10}\).
Zadanie 17. (3pkt) Podczas druku książki o nakładzie \(15\) tysięcy sztuk zniszczyło się \(1,4\%\) przygotowanego papieru. Jeden egzemplarz książki zawiera \(9\) arkuszy papieru, sprzedawanego w ryzach zawierających \(500\) arkuszy. Do wydrukowania całego nakładu przygotowano \(275\) ryz papieru. Oblicz, ile arkuszy papieru pozostało po wydrukowaniu całego nakładu tej książki.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Mamy \(15\) tysięcy książek, a każda z nich składa się z \(9\) arkuszy papieru. To oznacza, że liczba zadrukowanych arkuszy jest równa:
$$15000\cdot9=135000$$
Do wydrukowania przygotowano \(275\) ryz papieru, a każda ryza to \(500\) arkuszy, więc liczba przygotowanych arkuszy jest równa:
$$275\cdot500=137500$$
Podczas druku zniszczono \(1,4\%\) przygotowanego papieru (uwaga - tu jest spora pułapka, bo mowa jest o przygotowanym papierze, a nie zużytym). Skoro przygotowano \(137500\) arkuszy papieru, to zniszczonych arkuszy jest w takim razie:
$$0,014\cdot137500=1925$$
Łącznie liczba arkuszy zużytych na druk książki oraz zniszczony papier jest równa:
$$135000+1925=136925$$
W treści zadania pytają się nas, ile zostało arkuszy, a więc skoro było \(137500\) arkuszy, a my zużyliśmy \(136925\), to zostało nam:
$$137500-136925=575$$
To oznacza, że zostało \(575\) arkuszy papieru.
Zadanie 18. (2pkt) Pole trójkąta o danych długościach boków: \(a, b, c\), można obliczyć według wzoru:
$$S=\sqrt{p(p-a)(p-b)(p-c)}$$
\(S\) – pole trójkąta, \(p\) – połowa obwodu trójkąta.
Wykorzystaj dany wzór, aby obliczyć pole trójkąta o bokach: \(6\), \(7\) i \(11\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Obliczenie połowy obwodu trójkąta.
Do naszego wzoru musimy podstawić m.in. wartość \(p\), czyli połowy obwodu trójkąta. Skoro ma to być trójkąt o bokach \(6\), \(7\) i \(11\), to nasze \(p\) będzie równe:
$$p=\frac{6+7+11}{2} \\
p=\frac{24}{2} \\
p=12$$
Krok 2. Obliczenie pola trójkąta.
Korzystając teraz z podanego wzoru na pole trójkąta, możemy zapisać, że:
$$S=\sqrt{12\cdot(12-6)(12-7)(12-11)} \\
S=\sqrt{12\cdot6\cdot5\cdot1} \\
S=\sqrt{360}$$
Otrzymany wynik jest już poprawny (i jak tak to zostawimy, to nic się nie stanie), ale dobrą praktyką byłoby jeszcze wyłączenie czynnika przed znak pierwiastka, zatem:
$$S=\sqrt{360}=\sqrt{36\cdot10}=6\sqrt{10}$$
Zadanie 19. (3pkt) W przepisie na surówkę stosunek ilości kapusty do ilości marchewki wynosi \(7:3\). Według tego przepisu jedna porcja otrzymanej surówki waży \(18 dag\). Oblicz, ile dekagramów kapusty i ile dekagramów marchewki należy przygotować, aby wykonać \(15\) porcji takiej surówki.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Obliczenie ile dekagramów surówki trzeba przygotować.
Jedna porcja surówki waży \(18dag\), więc \(15\) porcji surówki będzie ważyć:
$$15\cdot18dag=270dag$$
Krok 2. Obliczenie ile dekagramów kapusty i marchewki trzeba przygotować.
Jeżeli stosunek ilości kapusty do ilości marchewki wynosi \(7:3\), to możemy zapisać, że:
\(7x\) - tyle potrzeba kapusty
\(3x\) - tyle potrzeba marchewki
Skoro nasze składniki mają łącznie ważyć \(270dag\), to:
$$7x+3x=270dag \\
10x=270dag \\
x=27dag$$
Teraz zgodnie z oznaczeniami, możemy zapisać, że:
Kapusta: \(7\cdot27dag=189dag\)
Marchewka: \(3\cdot27dag=81dag\)