Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro tangens jest równy \(\frac{3}{4}\), a przeciwprostokątna ma długość \(30\), to znaczy że zajdzie taka oto sytuacja:
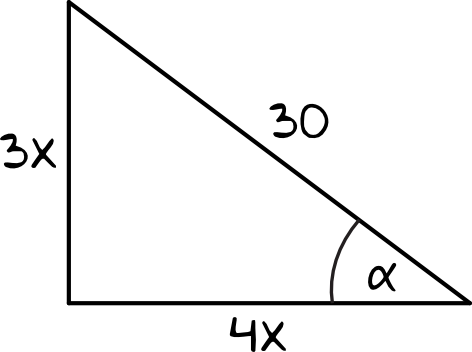
Krok 2. Obliczenie wartości niewiadomej \(x\).
Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$(3x)^2+(4x)^2=30^2 \\
9x^2+16x^2=900 \\
25x^2=900 \\
x^2=36 \\
x=6 \quad\lor\quad x=-6$$
Wartość ujemną oczywiście odrzucamy, zatem zostaje nam \(x=6\).
Krok 3. Obliczenie długości krótszej przyprostokątnej.
Krótsza przyprostokątna ma długość \(3x\), czyli \(3\cdot6=18\).