Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Musimy rozpatrzeć dwie sytuacje - pierwszą kiedy prostopadłościan leży na boku o największej powierzchni (wiemy, że wtedy słup wody sięga wysokości \(4cm\)) i drugą, kiedy leży na boku o najmniejszej powierzchni (tutaj poszukujemy wysokości słupa wody).
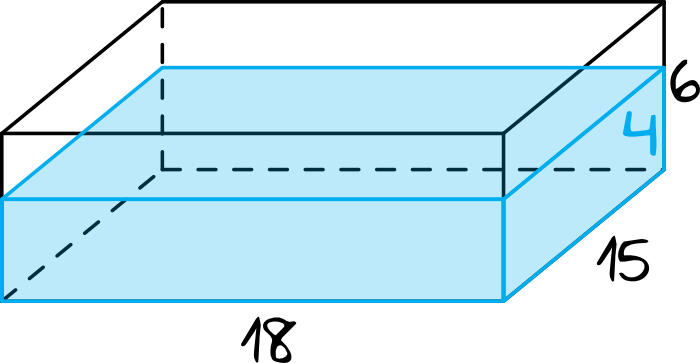
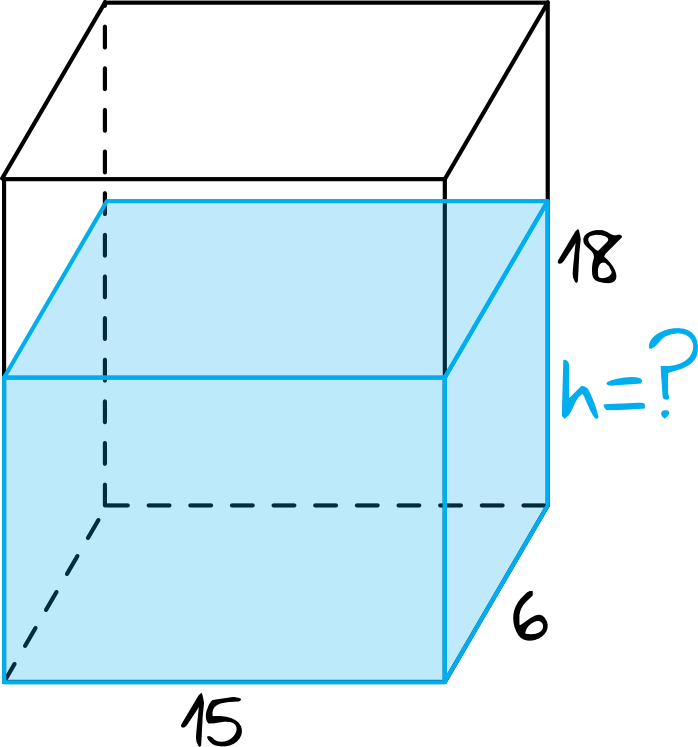
Objętość wody w jednym i drugim przypadku musi być jednakowa, zatem skoro możemy obliczyć objętość wody w pierwszym przypadku (a możemy, bo znamy wszystkie wymiary), to bez przeszkód obliczymy wysokość słupa wody w drugiej sytuacji.
Krok 2. Obliczenie objętości wody.
Objętość wody (nie prostopadłościanu!) wynosi:
$$V=18\cdot15\cdot4 \\
V=1080[cm^3]$$
Krok 3. Wyznaczenie wysokości słupa w drugim przypadku.
Pole podstawy drugiego prostopadłościanu jest równe:
$$P_{p}=15\cdot6 \\
P_{p}=90[cm^2]$$
Skoro wiemy, że objętość wody wynosi \(1080cm^3\). to możemy zapisać, że:
$$V=P_{p}\cdot H \\
1080cm^3=90cm^2\cdot H \\
H=12cm$$