Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Pamiętając o tym, że przekątna kwadratu o boku \(a\) ma długość \(a\sqrt{2}\) możemy sporządzić następujący rysunek:
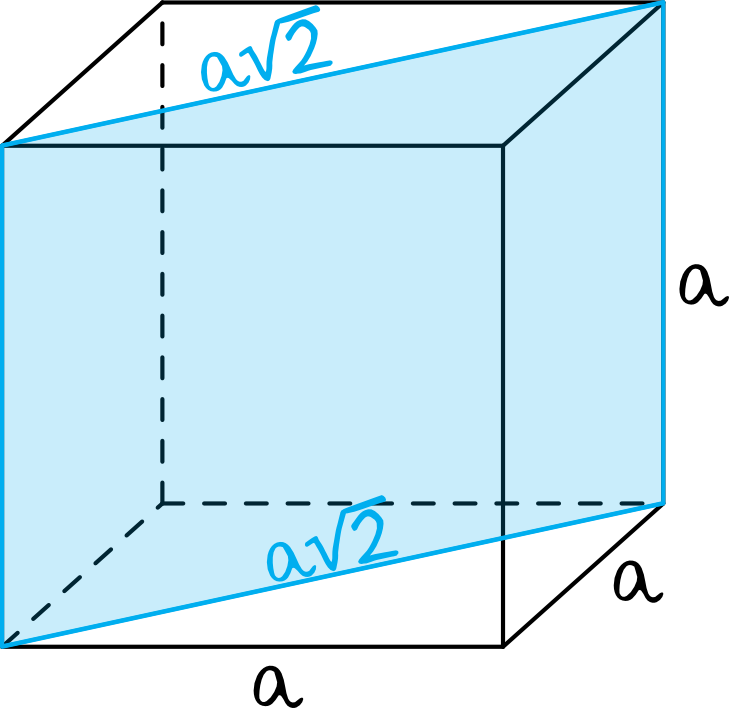
Krok 2. Obliczenie długości krawędzi sześcianu.
Nasz otrzymany przekrój jest prostokątem o wymiarach \(a\) oraz \(a\sqrt{2}\), zatem:
$$P=a\cdot a\sqrt{2} \\
16=a\cdot a\sqrt{2} \\
16=a^2\sqrt{2} \\
a^2=\frac{16}{\sqrt{2}}$$
Biorąc pod uwagę fakt, że pole całkowite sześcianu jest równe \(P_{c}=6a^2\) to nie ma za bardzo sensu pierwiastkować i obliczać ile jest równe \(a\), skoro za chwilę będziemy znowu potrzebować \(a^2\). Możemy pozostać przy wyliczeniu \(a^2\), ale usuńmy jeszcze niewymierność z mianownika:
$$a^2=\frac{16}{\sqrt{2}} \\
a^2=\frac{16\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a^2=\frac{16\sqrt{2}}{2} \\
a^2=8\sqrt{2}$$
Krok 3. Obliczenie pola całkowitego sześcianu.
Zgodnie z tym co zapisaliśmy sobie wcześniej:
$$P_{c}=6a^2 \\
P_{c}=6\cdot8\sqrt{2} \\
P_{c}=48\sqrt{2}$$