Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczmy sobie przekrój, którego pole musimy policzyć i nanieśmy na rysunek dane, które pozwolą nam wykonać obliczenia.
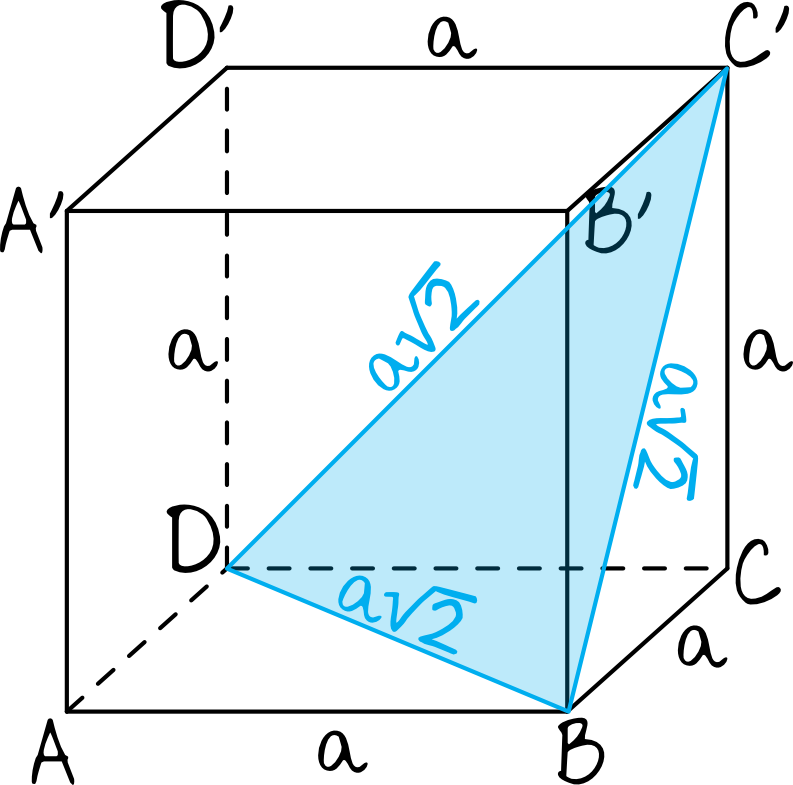
Okazuje się, że każdy bok trójkąta jest przekątną jakiegoś kwadratu, a z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\) (stąd też te miary pojawiły się już na rysunku). To z kolei prowadzi nas do bardzo ciekawego wniosku, a mianowicie że jest to trójkąt równoboczny o bokach długości \(a\sqrt{2}\).
Krok 2. Obliczenie pola powierzchni przekroju.
Korzystając ze wzoru na pole trójkąta \(P=\frac{a^2\sqrt{3}}{4}\) możemy bez problemu obliczyć pole naszego przekroju. Trzeba tylko być ostrożnym, bo trochę niefortunnie mamy tutaj zbieżność symboli i pod \(a\) będziemy podstawiać długość \(a\sqrt{2}\).
$$P=\frac{(a\sqrt{2})^2\cdot\sqrt{3}}{4} \\
P=\frac{a^2\cdot2\cdot\sqrt{3}}{4} \\
P=\frac{a^2\cdot\sqrt{3}}{2} \\
P=\frac{1}{2}a^2\sqrt{3}$$