Styczną do okręgu \((x-1)^2+y^2-4=0\) jest prosta o równaniu:
Równanie okręgu w postaci \((x-a)^2+(y-b)^2=r^2\) opisuje okrąg o długości promienia \(r\), którego środek znajduje się w punkcie \(S=(a;b)\).
Nasze równanie z treści zadania nie do końca jest identyczne jak pożądana postać, dlatego musimy przenieść liczbę \(4\) na prawą stronę i zapisać całość jako:
$$(x-1)^2+y^2-4=0 \\
(x-1)^2+(y-0)^2=4 \\
(x-1)^2+(y-0)^2=2^2$$
To oznacza, że okrąg ma promień \(r=2\) oraz współrzędne środka wynoszą \(S=(1;0)\).
Naszkicujmy nasz okrąg oraz styczne podane w odpowiedziach. Dzięki temu zobaczymy która z odpowiedzi jest poprawna.
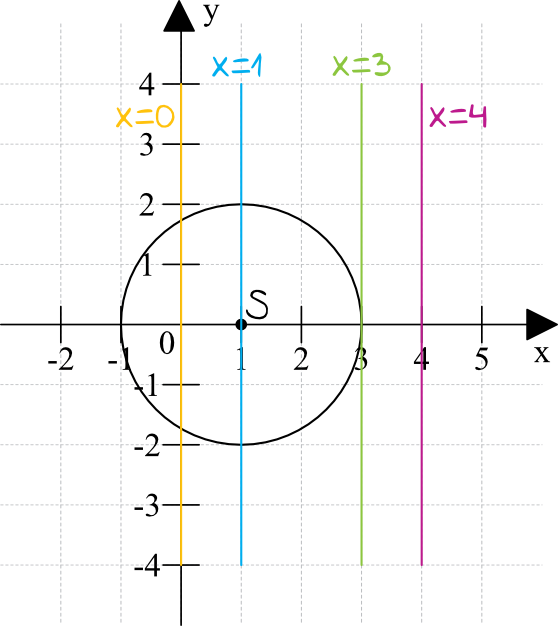
Widzimy wyraźnie, że poszukiwaną prostą styczną do tego okręgu jest \(x=3\).
Tak na marginesie to bez problemu możemy odczytać równania innych prostych stycznych do okręgu np. \(x=-1\), \(y=-2\), \(y=2\), ale ich akurat nie mieliśmy w naszych proponowanych odpowiedziach.
B. \(x=3\)

