Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych \(13\) i \(15\) wokół dłuższej przyprostokątnej. Promień podstawy tego stożka jest równy:
\(15\)
\(13\)
\(7,5\)
\(6,5\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
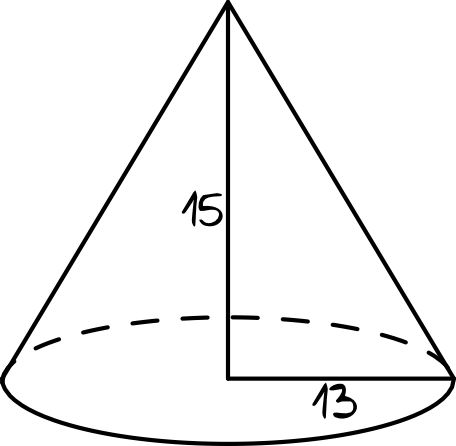
Krok 2. Odczytanie odpowiedzi z rysunku.
Z rysunku jasno wynika, że promień podstawy tego stożka jest równy długości krótszej przyprostokątnej, a więc \(13\).
Odpowiedź:
B. \(13\)

