Statystyka - Klasa 8
Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Statystyka. W teście znajduje się 14 zadań, a każde z nich jest warte 1 lub 2 punkty. Łącznie do uzyskania jest 20 punktów. Całość powinna Ci zająć maksymalnie 20-25 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Poniższa tabela prezentuje liczbę gości w restauracji Karo. Co jest prawdą na temat gości odwiedzających tę restaurację w analizowanym tygodniu?

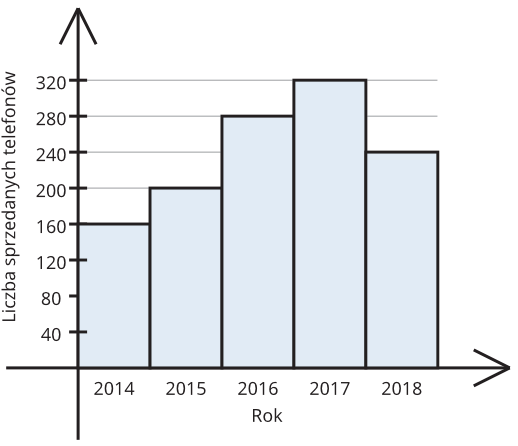
Zadanie 2. (1pkt) O ile procent wzrosła sprzedaż telefonów w sklepie Pana Jacka w 2018 roku względem 2015?
Zadanie 3. (1pkt) Poniżej znajduje się tabela, która pokazuje średnią temperaturę powietrza w danym miesiącu:
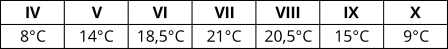
Którą z tych informacji możemy odczytać z tej tabeli?
Zadanie 4. (1pkt) Jaś rzucił \(30\) razy monetą. Częstość wypadnięcia reszki wyniosła \(\frac{3}{5}\). Ile razy Jaś wyrzucił w takim razie orła?
Zadanie 5. (1pkt) W finale piłkarskiego turnieju o Puchar Dyrektora Szkoły drużyna Białych grała z drużyną Czerwonych. Ile różnych wyników mogło paść w tym meczu, jeżeli wiemy że padły trzy bramki?
Zadanie 6. (1pkt) Na wykresie kołowym \(1\%\) wartości odpowiada mierze kąta wewnętrznego \(3,6°\).
Zadanie 7. (1pkt) Jeżeli frekwencja wyborcza wyniosła \(75\%\) to oznacza, że co czwarty wyborca nie wziął udziału w głosowaniu.
Zadanie 8. (1pkt) Na loterii fantowej obowiązuje zasada, że aby wygrać to trzeba na sześciennej kostce wyrzucić wynik większy niż \(4\). To oznacza, że prawdopodobieństwo wygranej jest równe \(p=\frac{1}{2}\).
Zadanie 9. (2pkt) Przed Mistrzostwami Świata dzieci zorganizowały mały konkurs. Każda z \(32\) osób wylosowała jedną z \(32\) drużyn, przy czym każda reprezentacja mogła być wylosowana tylko raz. Po zakończeniu Mistrzostw dziecko, które wylosowało zwycięzcę turnieju otrzyma kosz pełen nagród. Nie wszystkim jednak ta zabawa się spodobała. Jaś który bardzo chciał wylosować Hiszpanię uważa, że osoby losujące pod koniec kolejki mają mniejsze szanse na zwycięstwo, bo może się okazać że pierwsze osoby wylosują najlepsze drużyny, w tym właśnie jego ulubioną Hiszpanię. Małgosia uważa, że wszystko jest w porządku i że każdy (zarówno pierwszy jak i ostatni uczestnik) ma dokładnie takie same szanse na wylosowanie Hiszpanii, czy też innej czołowej reprezentacji. Kto ma rację?
Zadanie 10. (2pkt) W klasie 8a nauczycielka przeprowadziła konkurs na który przygotowała \(24\) pytania łatwe, \(16\) średnich oraz \(20\) trudnych. Dzieci po kolei podchodziły do stolika, losowały pytanie, po czym kartka z wykorzystanym pytaniem została wyrzucona. Pierwszy losował Jaś, trafił na pytanie średniej trudności. Teraz do losowania podchodzi Małgosia. Jaś twierdzi, że Małgosia ma większe szanse na trafienie trudnego pytania niż miał on sam. Małgosia uważa, że szanse są takie same, bo przed jej losowaniem jest tyle samo pytań trudnych, ile było przed losowaniem Jasia. Kto ma rację?
Zadanie 11. (2pkt) Rzucamy dwiema monetami. Ile jest wszystkich możliwych kombinacji wyników takiego rzutu, w których wypadnie przynajmniej jeden orzeł?
Zadanie 12. (2pkt) Ania przeczytała lekturę w ciągu \(10\) dni, a poniższy wykres pokazuje jej dzienne tempo czytania tej książki.
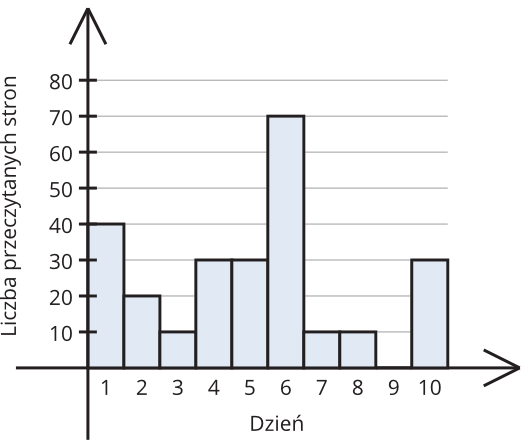
Po analizie wykresu możemy stwierdzić, że:
Zadanie 13. (2pkt) W pudełku znalazły się piłki białe i czarne. Stosunek piłek białych do czarnych jest równy \(5:4\). Jakie jest prawdopodobieństwo wylosowania piłki białej?
Zadanie 14. (2pkt) Zdarzenie pewne to takie, którego prawdopodobieństwo wystąpienia jest równe \(p=1\). Przykładem takiego zdarzenia będzie:

SUPER!!!
Wyśmienity test.
Superancki Test! bardzo pomógł przed spr :D