Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować tę sytuację, tak aby mieć lepszy ogląd całej sytuacji:
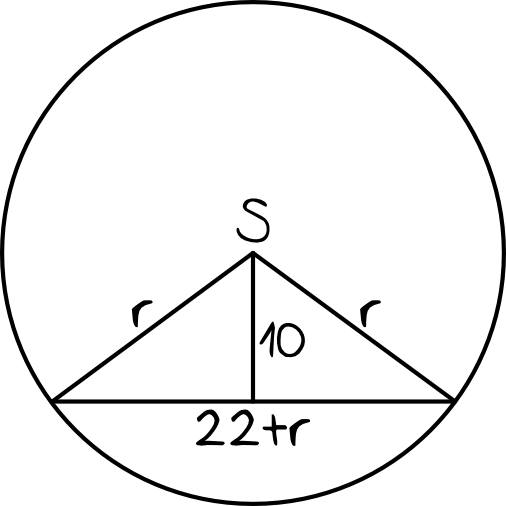
Patrząc się na rysunek widzimy, że powstał nam trójkąt, który jest równoramienny. Skąd wiadomo, że jest on równoramienny? Po prostu jego ramiona są promieniami naszego okręgu, czyli mają jednakową miarę.
Teraz przeanalizujmy odcinek, który łączy środek okręgu i cięciwę. Zgodnie z treścią zadania ma on długość równą \(10\). Z podstaw geometrii wiemy, że odległość z punktu do prostej jest zawsze linią prostopadłą do prostej, nie ma innej możliwości. To sprawia, że ten omawiany odcinek jest tak naprawdę wysokością naszego trójkąta równoramiennego.
Z własności trójkątów równoramiennych wiemy, że wysokość takiego trójkąta dzieli podstawę na dwie równe części, czyli powstaje nam taki oto trójkąt prostokątny:
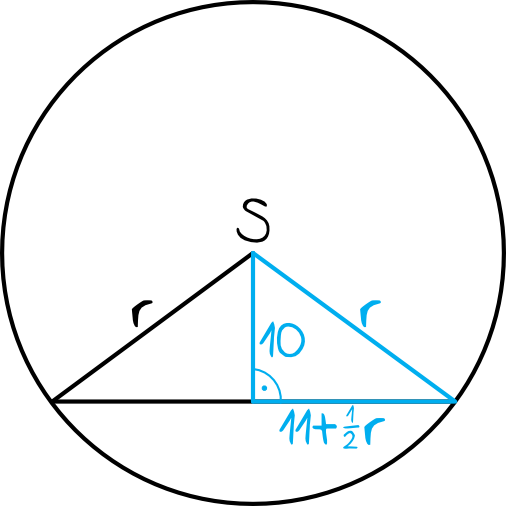
Krok 2. Ułożenie równania kwadratowego.
Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$\left(11+\frac{1}{2}r\right)^2+10^2=r^2 \\
121+11r+\frac{1}{4}r^2+100=r^2 \\
\frac{1}{4}r^2+11r+221=r^2 \quad\bigg/\cdot4 \\
r^2+44r+884=4r^2 \\
-3r^2+44r+884=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego i wyznaczenie długości promienia okręgu.
Współczynniki: \(a=-3,\;b=44,\;c=884\)
$$Δ=b^2-4ac=44^2-4\cdot(-3)\cdot884=1936+10608=12544 \\
\sqrt{Δ}=\sqrt{12544}=112$$
$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-44-112}{2\cdot(-3)}=\frac{-156}{-6}=26 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-44+112}{2\cdot(-3)}=\frac{68}{-6}=-11\frac{1}{3}$$
Otrzymaliśmy dwie możliwości długości promienia, ale jedną z nich musimy odrzucić, bo promień nie może mieć ujemnej długości. W związku z tym jedyną poprawną odpowiedzią będzie \(r=26\).