Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zastanówmy się jakie odcinki mogą nam wyjść kiedy wylosujemy dwa wierzchołki sześciokąta. Możemy spotkać się z jedną z trzech sytuacji:

• w pierwszej sytuacji kiedy wylosowane punkty są sąsiadującymi wierzchołkami to otrzymamy odcinek o długości \(1\).
• w drugiej sytuacji wylosowane punkty mogą utworzyć dłuższą przekątną sześciokąta. Jej długość jest równa \(1+1=2\), co widać wyraźnie na naszym rysunku (dłuższe przekątne podzieliły nam sześciokąt na sześć trójkątów równobocznych).
• w trzeciej sytuacji wylosowane punkty mogą utworzyć krótszą przekątną sześciokąta. Jej długość jest zgodnie z własnościami trójkątów o kątach \(30°,60°,90°\) równa \(\sqrt{3}\).
Krok 2. Ustalenie liczby wszystkich możliwych zdarzeń elementarnych.
Analizując nasz sześciokąt możemy dostrzec, że losując dwa dowolne wierzchołki możemy otrzymać:
• \(6\) boków o długości \(1\) (to będą boki sześciokąta)
• \(3\) dłuższe przekątne o długości \(2\)
• \(6\) krótszych przekątnych o długości \(\sqrt{3}\) (utworzą one taką gwiazdkę)
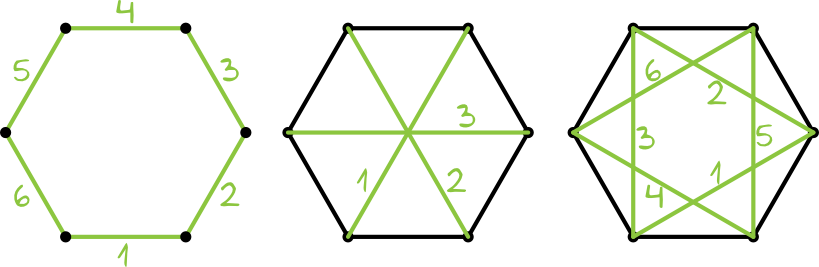
Łącznie jest to \(6+3+6=15\) różnych odcinków. Możemy więc zapisać, że \(|Ω|=15\).
Krok 3. Ustalenie liczby zdarzeń sprzyjających.
Zdarzeniami sprzyjającymi będzie wylosowanie odcinka o długości niewymiernej, czyli w tym przypadku o długości \(\sqrt{3}\). Mamy takich \(6\) odcinków, zatem \(|A|=6\).
Krok 4. Obliczenie prawdopodobieństwa.
Prawdopodobieństwo obliczymy korzystając ze wzoru:
$$P(A)=\frac{|A|}{|Ω|}=\frac{6}{15}=\frac{2}{5}$$
UWAGA: Zadanie jest dość mylące, bowiem tak prawdę mówiąc nigdzie nie jest powiedziane, że nie można byłoby wylosować dwóch tych samych wierzchołków i tym samym długość takiego odcinka byłaby równa \(0\). Powiększyłaby nam się w ten sposób o \(6\) liczba możliwych zdarzeń elementarnych. Moim zdaniem jeżeli ktoś na prawdziwej maturze obliczyłby to zadanie w taki sposób, otrzymując prawdopodobieństwo równe \(\frac{6}{21}=\frac{2}{7}\), to zadanie też byłoby uznane.