Rozwiązanie
Krok 1. Obliczenie długości krawędzi podstawy.
Ostrosłup jest prawidłowy czworokątny, czyli w podstawie bryły znajduje się kwadrat. O tym kwadracie wiemy, że jego pole jest równe \(4\), zatem bok kwadratu (a tym samym długość krawędzi podstawy) będzie równa:
$$P=a^2 \\
a^2=4 \\
a=2 \quad\lor\quad a=-2$$
Ujemną wartość oczywiście odrzucamy, zatem zostaje nam \(a=2\).
Krok 2. Obliczenie wysokości trójkąta znajdującego się w ścianie bocznej.
Wiemy już, że krawędź podstawy jest równa \(2\), zatem trójkąty znajdujące się w ścianie bocznej mają także podstawę równą \(2\). Wiemy też, że pole każdego takiego trójkąta jest równe \(4\), zatem:
$$P=\frac{1}{2}ah \\
4=\frac{1}{2}\cdot2\cdot h \\
4=1\cdot h \\
h=4$$
Krok 3. Sporządzenie rysunku pomocniczego.
Ostrosłup jest prawidłowy, zatem ściany boczne będą w tym przypadku trójkątami równoramiennymi. Wiedząc, że wysokość w takich trójkątach dzieli podstawę na dwie równe części, to powstała nam następująca sytuacja:
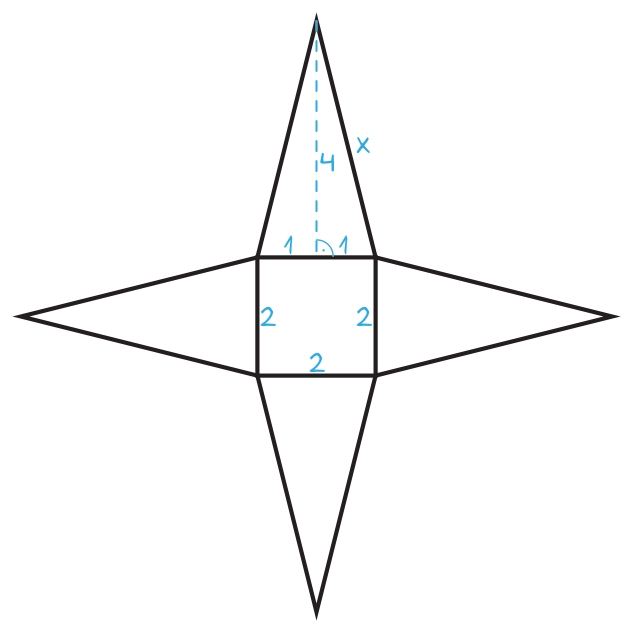
Krok 4. Obliczenie długości krawędzi bocznej.
Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$1^2+4^2=x^2 \\
1+16=x^2 \\
x^2=17 \\
x=\sqrt{17} \quad\lor\quad x=-\sqrt{17}$$
Ujemną wartość odrzucamy, bo długość krawędzi nie może być ujemna, zatem zostaje nam \(x=\sqrt{17}\).