Rysunek przedstawia fragment siatki ostrosłupa prawidłowego czworokątnego, którego wszystkie krawędzie mają po 2 cm długości

Rysunek przedstawia fragment siatki ostrosłupa prawidłowego czworokątnego, którego wszystkie krawędzie mają po $2 cm$ długości.

a) Uzupełnij powyższy rysunek – dorysuj brakujący element siatki ostrosłupa.

b) Oblicz łączną długość wszystkich krawędzi tego ostrosłupa.

Rozwiązanie

a) Uzupełniona siatka może wyglądać następująco:
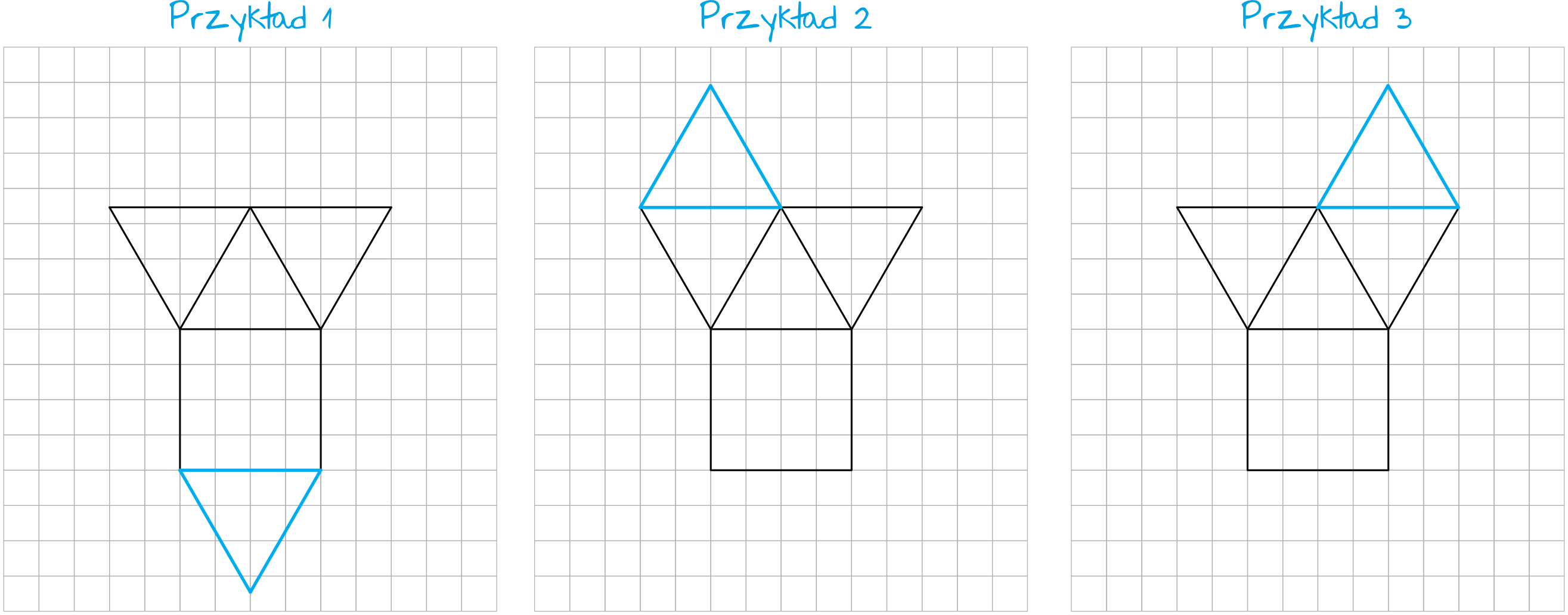
egzamin ósmoklasisty

b) Ostrosłup mający w podstawie czworokąt (czyli liczba boków wynosi $n=4$) będzie mieć osiem krawędzi (bo liczba krawędzi ostrosłupa jest równa $2n$, czyli $2\cdot4=8$). Skoro każda krawędź ma długość $2cm$, to łączna suma krawędzi wyniesie:
$$8\cdot2cm=16cm$$

Odpowiedź

a) są trzy możliwości (patrz rysunek)
b) $16cm$

Zadania

Rysunek przedstawia fragment siatki ostrosłupa prawidłowego czworokątnego, którego wszystkie krawędzie mają po 2 cm długości

Rysunek przedstawia fragment siatki ostrosłupa prawidłowego czworokątnego, którego wszystkie krawędzie mają po \(2 cm\) długości.

a) Uzupełnij powyższy rysunek – dorysuj brakujący element siatki ostrosłupa.

b) Oblicz łączną długość wszystkich krawędzi tego ostrosłupa.

Rysunek przedstawia fragment siatki ostrosłupa prawidłowego czworokątnego, którego wszystkie krawędzie mają po \(2 cm\) długości. a) Uzupełnij powyższy rysunek – dorysuj brakujący element siatki ostrosłupa. b) Oblicz łączną długość wszystkich krawędzi tego ostrosłupa.

Rysunek przedstawia fragment siatki ostrosłupa prawidłowego czworokątnego, którego wszystkie krawędzie mają po \(2 cm\) długości.

a) Uzupełnij powyższy rysunek – dorysuj brakujący element siatki ostrosłupa.

b) Oblicz łączną długość wszystkich krawędzi tego ostrosłupa.