Rozwiąż nierówność x^2-8x+7≥0

Rozwiąż nierówność \(x^2-8x+7\ge0\).

Do obliczenia tej nierówności skorzystamy z metody delty.
Współczynniki: \(a=1,\;b=-8,\;c=7\)
$$Δ=b^2-4ac=(-8)^2-4\cdot1\cdot7=64-28=36 \\
\sqrt{Δ}=\sqrt{36}=6$$

$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-8)-6}{2\cdot1}=\frac{8-6}{2}=\frac{2}{2}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-8)+6}{2\cdot1}=\frac{8+6}{2}=\frac{14}{2}=7$$

Ramiona paraboli będą skierowane do góry, bo współczynnik \(a\) jest dodatni. Zaznaczamy miejsca zerowe obliczone przed chwilą i szkicujemy parabolę. Kropki przy miejscach zerowych będą zamalowane bo w nierówności wystąpił znak \(\ge\).

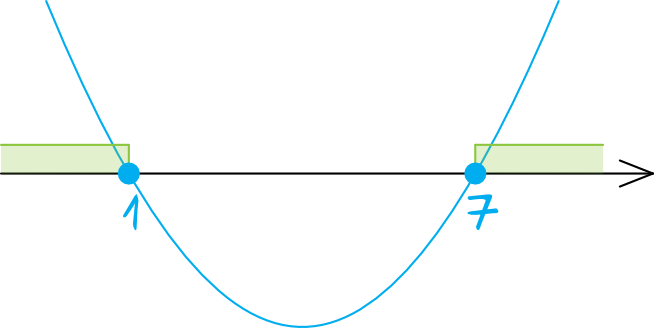
Interesują nas wartości większe lub równe zero. W związku z tym rozwiązaniem będzie następujący przedział: \(x\in(-\infty;1\rangle\cup\langle7;+\infty)\).

\(x\in(-\infty;1\rangle\cup\langle7;+\infty)\)