Rozwiąż nierówność \(x^2-3x-10\lt0\).
Rozwiązanie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=1,\;b=-3,\;c=-10\)
$$Δ=b^2-4ac=(-3)^2-4\cdot1\cdot(-10)=9-(-40)=9+40=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-3)-7}{2\cdot1}=\frac{3-7}{2}=\frac{-4}{2}=-2 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-3)+7}{2\cdot1}=\frac{3+7}{2}=\frac{10}{2}=5$$
Krok 2. Szkicowanie wykresu paraboli.
Ramiona paraboli będą skierowane do góry, bo współczynnik \(a\) jest dodatni. Zaznaczamy więc na osi liczbowej miejsca zerowe wyznaczone w pierwszym kroku. Kropki przy miejscach zerowych będą niezamalowane, bo w nierówności wystąpił znak \(\lt\).
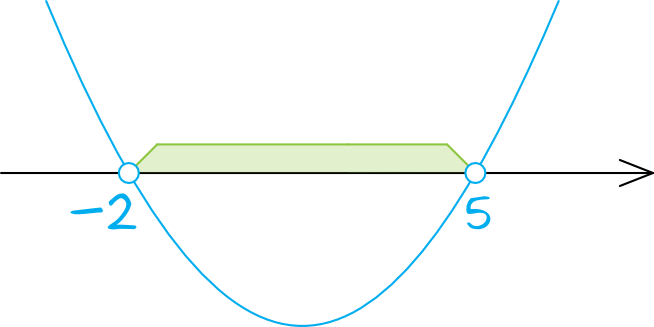
Krok 3. Odczytanie rozwiązania.
Interesują nas wartości mniejsze od zera, czyli takie, które znalazły się pod osią \(Ox\). To oznacza, że rozwiązaniem zadania będzie przedział: \(x\in(-2;5)\).
Odpowiedź:
\(x\in(-2;5)\)

