Rozwiąż nierówność \(x^2+11x+30\le0\).
Rozwiązanie:
Krok 1. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=1,\;b=11,\;c=30\)
$$Δ=b^2-4ac=11^2-4\cdot1\cdot30=121-120=1 \\
\sqrt{Δ}=\sqrt{1}=1$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-11-1}{2\cdot1}=\frac{-12}{2}=-6 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-11+1}{2\cdot1}=\frac{-10}{2}=-5$$
Krok 2. Szkicowanie wykresu paraboli.
Parabola ma ramiona skierowane ku górze, bo współczynnik \(a\) jest dodatni. Wykres będzie miał więc następującą postać:
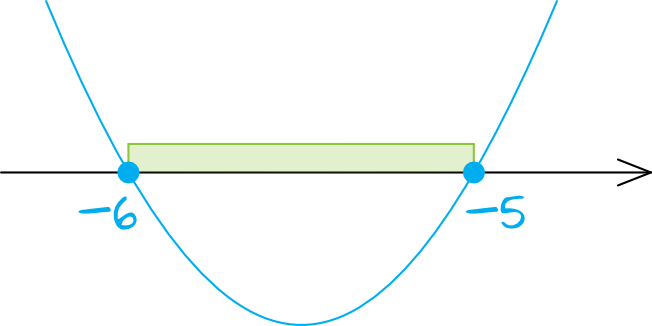
Punkty \(x=-6\) oraz \(x=-5\) muszą mieć koniecznie zamalowane kropki, bo w nierówności wystąpił znak \(\le\).
Krok 3. Odczytanie rozwiązania nierówności.
Interesuje nas zbiór argumentów, dla których wartość funkcji kwadratowej jest mniejsza lub równa zero (czyli w których miejscach wykres funkcji jest pod osią \(Ox\) lub dokładnie na osi). Tym zbiorem jest oczywiście: \(x\in\langle-6;-5\rangle\).
Odpowiedź:
\(x\in\langle-6;-5\rangle\)

