Rozwiązanie
Krok 1. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=-9,\;b=6,\;c=-1\)
$$Δ=b^2-4ac=6^2-4\cdot(-9)\cdot(-1)=36-36=0$$
Skoro delta jest ujemna, to mamy tylko jedno miejsce zerowe:
$$x_{1}=\frac{-b}{2a}=\frac{-6}{2\cdot(-9)}=\frac{-6}{-18}=\frac{1}{3}$$
Krok 2. Szkicowanie wykresu paraboli.
Współczynnik \(a\) jest ujemny, więc parabola ma skierowane ramiona do dołu. Zaznaczamy na osi miejsce zerowe, które przed chwilą obliczyliśmy (kropka będzie niezamalowana, bo w nierówności wystąpił znak \(\lt\)) i szkicujemy wykres paraboli:
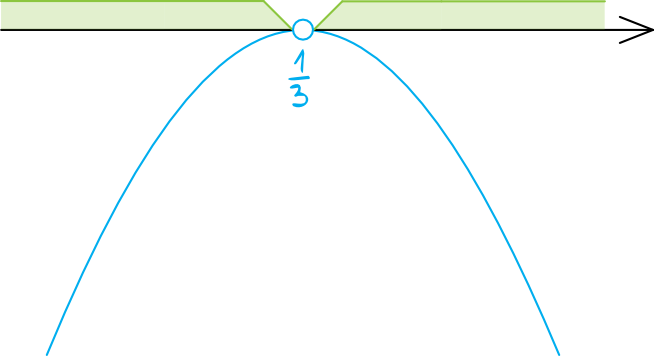
Krok 3. Odczytanie rozwiązania.
Interesuje nas przedział dla których zbiór argumentów przyjmuje wartość mniejszą od zera, czyli patrzymy na to co znalazło się pod osią. Okazuje się, że rozwiązaniem tej nierówności będzie każda liczba, tylko nie \(\frac{1}{3}\), dla której to wielomian przyjął wartość równą \(0\). To oznacza, że rozwiązaniem tej nierówności jest zbiór: \(x\in\mathbb{R}\backslash\{\frac{1}{3}\}\) lub też jak kto woli \(x\in(-\infty;\frac{1}{3})\cup(\frac{1}{3};+\infty)\).