Rozwiązanie
Krok 1. Zapisanie nierówności w postaci ogólnej.
Rozwiązywanie należy zacząć od przekształcenia nierówności, tak aby po prawej stronie otrzymać zero. Odejmując obustronnie \(3\), otrzymamy:
$$3x^2-8x\ge3 \\
3x^2-8x-3\ge0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Teraz możemy przystąpić do obliczenia miejsc zerowych, korzystając z tradycyjnej delty.
Współczynniki: \(a=3,\;b=-8,\;c=-3\)
$$Δ=b^2-4ac=(-8)^2-4\cdot3\cdot(-3)=64-(-36)=100 \\
\sqrt{Δ}=\sqrt{100}=10$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-8)-10}{2\cdot3}=\frac{8-10}{6}=\frac{-2}{6}=-\frac{1}{3} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-8)+10}{2\cdot3}=\frac{8+10}{6}=\frac{18}{6}=3$$
Krok 3. Szkicowanie wykresu paraboli.
Parabola będzie mieć ramiona skierowane do góry, bo współczynnik \(a\) jest dodatni. Zaznaczając na osi obliczone miejsca zerowe, otrzymamy taką oto sytuację:
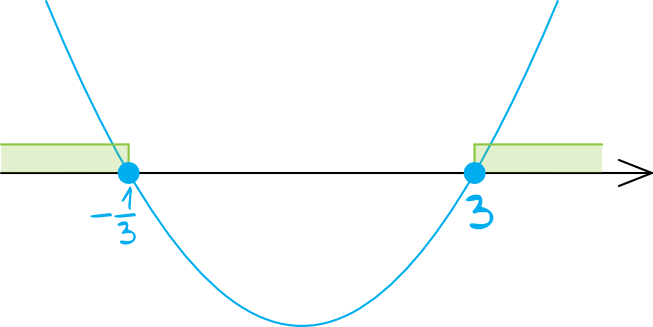
Krok 4. Odczytanie rozwiązania.
Interesują nas miejsca w których funkcja przyjmuje wartości większe lub równe zero. Patrzymy się zatem co znajduje się nad osią lub na osi i widzimy, że rozwiązaniem tej nierówności będzie w takim razie \(x\in(-\infty; -\frac{1}{3}\rangle\cup \langle3;+\infty)\).