Rozwiąż nierówność \(-3x^2+3x+36\ge0\).
Miejsca zerowe najprościej będzie obliczyć tzw. metodą delty:
Współczynniki: \(a=-3,\;b=3,\;c=36\)
$$Δ=b^2-4ac=3^2-4\cdot(-3)\cdot36=9+432=441 \\
\sqrt{Δ}=\sqrt{441}=21$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-3-21}{2\cdot(-3)}=\frac{-24}{-6}=4 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-3+21}{2\cdot(-3)}=\frac{18}{-6}=-3$$
Współczynnik \(a\) jest ujemny bo jest równy \(-3\). To oznacza, że nasza parabola będzie mieć ramiona skierowane do dołu. Zaznaczamy na osi miejsca zerowe obliczone przed chwilą i szkicujemy wykres paraboli:
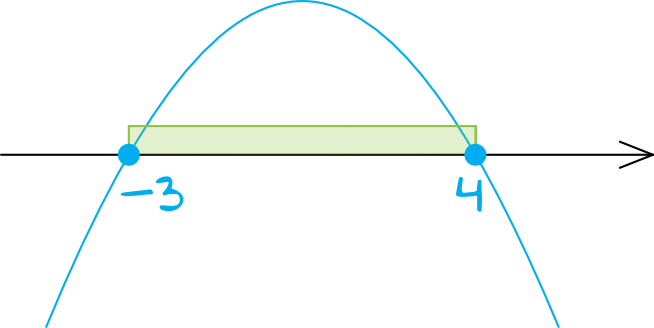
Punkty \(x=-3\) oraz \(x=4\) mają zamalowane kropki, bo w nierówności wystąpił znak \(\ge\).
Interesują nas wartości większe lub równe zero (czyli na osi lub nad nią) i widzimy, że funkcja przyjmuje takie wartości w przedziale \(x\in\langle-3;4\rangle\). To jest też nasza ostateczna odpowiedź.
\(x\in\langle-3;4\rangle\)

